C++ 实现无向图的最小生成树Prim算法(附完整代码)
Posted Wecccccccc
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C++ 实现无向图的最小生成树Prim算法(附完整代码)相关的知识,希望对你有一定的参考价值。
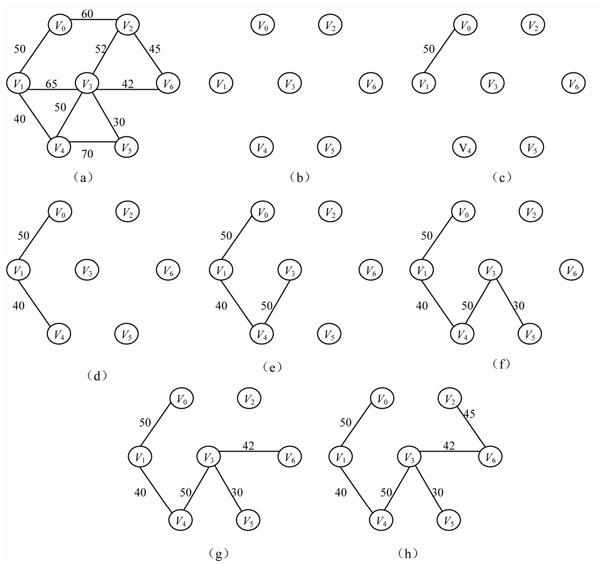
实现Prim算法,需设置两个辅助一维数组lowcost和closevertex。
- 其中lowcost用来保存集合V-U中各顶点与集合U中各顶点构成的边中具有最小权值的边的权值;
- 数组closevertex用来保存依附于该边的在集合U中的顶点。
过程:
假设初始状态时,U={u0}(u0为出发的顶点),这时有lowcost[0]=0,它表示顶点u0已加入集合U中,数组lowcost的其他各分量的值是顶点u0到其余各顶点所构成的直接边的权值。
然后不断选取权值最小的边(ui,uk)(ui∈U,uk∈V-U),每选取一条边,就将lowcost(k)置为0,表示顶点uk已加入集合U中。
由于顶点uk从集合V-U进入集合U后,这两个集合的内容发生了变化,就需依据具体情况更新数组lowcost和closevertex中部分分量的内容。
最后closevertex中即为所建立的最小生成树。
当无向网采用二维数组存储的邻接矩阵存储时,Prim算法的C++实现算法如下:
void MGraph::Min_Tree_Prim(int u)
{
for (int i = 0; i < vertexnum; i++)
if (i != u)
{
close_edge[i].adjvertex = u;
close_edge[i].lowcost = arcs[u][i];
}
close_edge[u].lowcost = 0;
int k;
for (int i = 0; i < vertexnum - 1; i++)
{
int w = MAXW;
for (int j = 0; j < vertexnum; j++)
{
if (close_edge[j].lowcost != 0 && close_edge[j].lowcost < w)
{
w = close_edge[j].lowcost;
k = j;
}
}
close_edge[k].lowcost = 0;
for (int j = 0;j<vertexnum;j++)
if (arcs[k][j] < close_edge[j].lowcost)
{
close_edge[j].adjvertex = k;
close_edge[j].lowcost = arcs[k][j];
}
}
for (int i = 0; i < vertexnum; i++)
if (i != u)
cout << i << "->" << close_edge[i].adjvertex << "," << arcs[i][close_edge[i].adjvertex] << endl;
}
完整代码如下:
#include <iostream>
#include <queue>
using namespace std;
typedef int VertexType;
typedef int EdgeType;
const int MaxVertexNum = 30;
const int MAXW = 1e8;
class closEdge
{
friend class MGraph;
private:
int adjvertex;
int lowcost;
};
class MGraph
{
public:
MGraph()
{
CreatGraph();
};
void Min_Tree_Prim(int u);
void CreatGraph();
void Visit(int v);
void BFS(int v);
void BFStraverse();
void DFStraverse();
bool Ispath_BFS(int i, int j);//判断结点i和结点j之间是否有路径
bool Ispath_DFS(int i, int j);//判断结点i和结点j之间是否有路径
void Init_vis();
private:
void DFS(int i, int j, bool &flag);
void dfs_graph(int i);
VertexType vertexs[MaxVertexNum];
EdgeType arcs[MaxVertexNum][MaxVertexNum];
int vertexnum;
int edgenum;
closEdge close_edge[MaxVertexNum];
bool vis[MaxVertexNum];
};
void MGraph::Min_Tree_Prim(int u)
{
for (int i = 0; i < vertexnum; i++)
if (i != u)
{
close_edge[i].adjvertex = u;
close_edge[i].lowcost = arcs[u][i];
}
close_edge[u].lowcost = 0;
int k;
for (int i = 0; i < vertexnum - 1; i++)
{
int w = MAXW;
for (int j = 0; j < vertexnum; j++)
{
if (close_edge[j].lowcost != 0 && close_edge[j].lowcost < w)
{
w = close_edge[j].lowcost;
k = j;
}
}
close_edge[k].lowcost = 0;
for (int j = 0;j<vertexnum;j++)
if (arcs[k][j] < close_edge[j].lowcost)
{
close_edge[j].adjvertex = k;
close_edge[j].lowcost = arcs[k][j];
}
}
for (int i = 0; i < vertexnum; i++)
if (i != u)
cout << i << "->" << close_edge[i].adjvertex << "," << arcs[i][close_edge[i].adjvertex] << endl;
}
void MGraph::CreatGraph()
{
Init_vis();
cout << "请输入图的顶点个数和边的条数" << endl;
cin >> vertexnum >> edgenum;
cout << "请依次输入按序号0到n顶点的中存储的信息" << endl;
for (int i = 0; i < vertexnum; i++) cin >> vertexs[i];
for (int i = 0; i < vertexnum; i++)
for (int j = 0; j < vertexnum; j++)
arcs[i][j] = MAXW;
cout << "请输入边的信息(该图以有向图的邻接矩阵存储方式存储)" << endl;
for (int i = 0; i < edgenum; i++)
{
int a1, a2, w;
cout << "输入边<i,j>对应的顶点序号i,j,然后再输入该边的权值" << endl;
cin >> a1 >> a2>>w;
arcs[a1][a2] = w;
arcs[a2][a1] = w;
}
}
void MGraph::Init_vis()
{
for (int i = 0; i < MaxVertexNum; i++) vis[i] = false;
}
void MGraph::Visit(int v)
{
cout << vertexs[v] << " ";
}
void MGraph::BFS(int v)
{
queue<int >q;
q.push(v);
vis[v] = true;
while (q.size())
{
int t = q.front();
Visit(t);
q.pop();
for (int i = 0; i < vertexnum; i++)
{
if (arcs[t][i] == 1 && vis[i] == false)
{
vis[i] = true;
q.push(i);
}
}
}
cout << endl;
Init_vis();
}
void MGraph::BFStraverse()
{
queue<int >q;
for (int i = 0; i < vertexnum; i++)
{
if (vis[i] == false)
{
vis[i] = true;
q.push(i);
while (q.size())
{
int t = q.front();
Visit(t);
q.pop();
for (int j = 0; j < vertexnum; j++)
if (arcs[t][j] == 1 && vis[j] == false)
{
vis[j] = true;
q.push(j);
}
}
}
}
cout << endl;
Init_vis();
}
void MGraph::dfs_graph(int i)
{
Visit(i);
for (int j = 0; j < vertexnum; j++)
{
if (arcs[i][j] == 1 && vis[j] == false)
{
vis[j] = true;
dfs_graph(j);
}
}
}
void MGraph::DFStraverse()
{
for (int i = 0; i < vertexnum; i++)
{
if (vis[i] == false)
{
vis[i] = true;
dfs_graph(i);
}
}
cout << endl;
Init_vis();
}
bool MGraph::Ispath_BFS(int i, int j)
{
queue<int >q;
vis[i] = true;
q.push(i);
while (q.size())
{
int t = q.front();
q.pop();
if (t == j)
{
Init_vis();
return true;
}
for (int k = 0; k < vertexnum; k++)
{
if (arcs[t][k] == 1 && vis[k] == false)
{
vis[k] = true;
q.push(k);
}
}
}
Init_vis();
return false;
}
void MGraph::DFS(int i, int j, bool &flag)
{
if (i == j)
{
flag = true;
return;
}
for (int k = 0; k < vertexnum; k++)
{
if (arcs[i][k] == 1 && vis[k] == false)
{
vis[k] = true;
DFS(k, j, flag);
vis[k] = false;
}
}
}
bool MGraph::Ispath_DFS(int i, int j)
{
bool flag = false;
vis[i] = true;
DFS(i, j, flag);
Init_vis();
if (flag) return true;
else return false;
}
int main()
{
MGraph g;
int v;
cin >> v;
g.BFS(v);
g.BFStraverse();
g.DFStraverse();
int n;
cin >> n;
g.Min_Tree_Prim(n);
return 0;
}
测试结果:
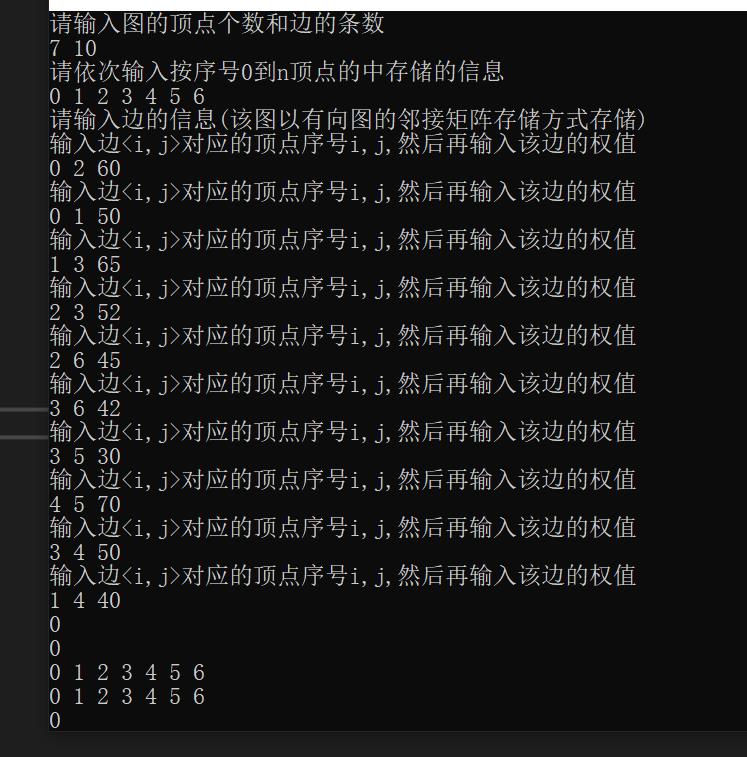

以上是关于C++ 实现无向图的最小生成树Prim算法(附完整代码)的主要内容,如果未能解决你的问题,请参考以下文章