二叉排序树(搜索树BST)-详解结点的删除

Posted 2021-05-16 Wecccccccc

在二叉排序树中删除一个结点时，需保证删除后的二叉树仍然是二叉排序树。为讨论方便，假定被删除结点为p，其双亲结点为f。删除的过程可按下述的两种情况分别处理。
在这里我们用红色三角形表示我们要删除的结点，蓝色表示我们要改变指针的指向，如果蓝色是圆圈，则说明是新根。
（1）如果被删除的结点没有左子树，则只需把结点f指向p的指针改为指向p的右子树。
情况一:

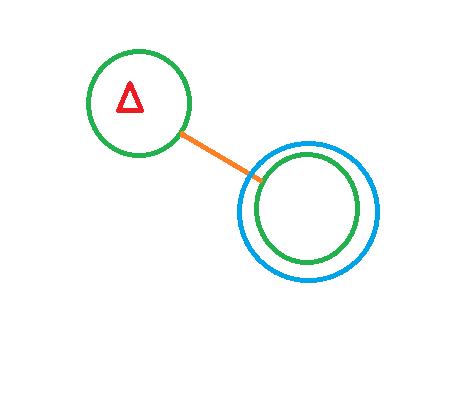
情况二:

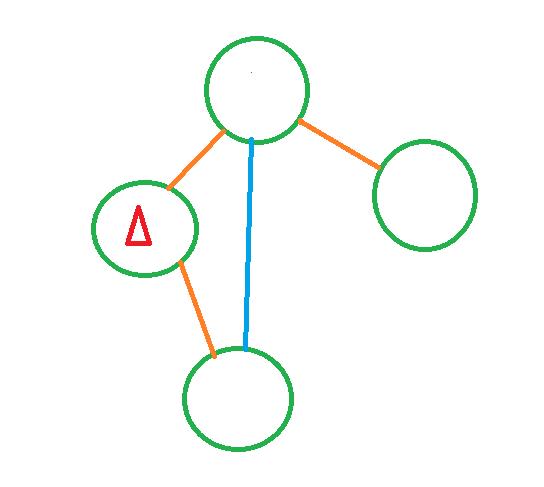
情况三:

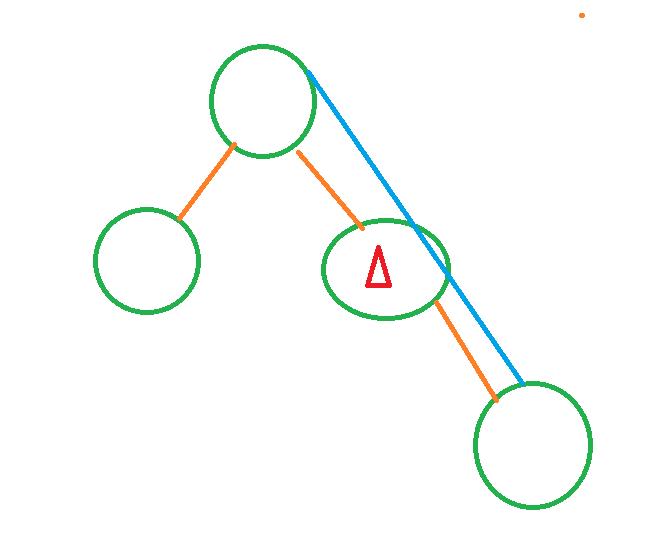
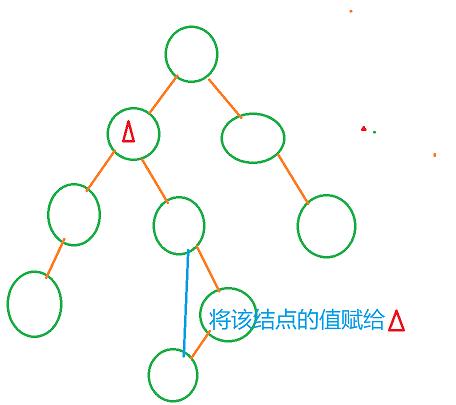
（2）如果被删除的结点p有左子树，则删除结点p时，从结点p的左子树中选择结点值最大的结点s（其实就是p的左子树中最右下角的结点，该结点s可能有左子树，但右子树一定为空），用结点s替换结点p（把s的数据复制到p中），再将指向结点s的指针改为指向结点s的左子树即可。

情况一:

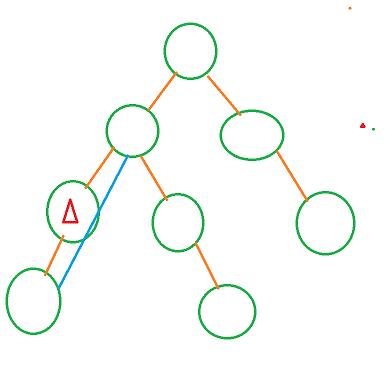
情况二:

代码如下:

bool BinSTree::BSTreeDelete(BinSTreeNode *&bt, KeyType k)
{
	BinSTreeNode *f, *p, *q, *s;
	p = bt;
	f = nullptr;
	while (p && p->key != k)
	{
		f = p;
		if (p->key > k) p = p->lchild;
		else p = p->rchild;
	}
	if (p == nullptr) return false;
	if (p->lchild == nullptr)//(1)
	{
		if (f == nullptr) bt = p->rchild;//情况一
		else if (f->lchild == p) f->lchild = p->rchild;//情况二
		else f->rchild = p->rchild;//情况三
		delete p;
		return true;
	}
	else//(2)
	{
		q = p;
		s = p->lchild;
		while (s->rchild)
		{
			q = s;
			s = s->rchild;
		}
		if (q == p) q->lchild = s->lchild;//情况一
		else q->rchild = s->lchild;//情况二
		p->key = s->key;
		delete s;
		return true;
	}
}