平衡二叉树(AVL树)-详解平衡调整

Posted 2021-05-16 Wecccccccc

平衡调整:
(注意：平衡调整只是平衡调整，没有进行结点的插入)

LL型调整:
(带阴影的小框表示插入的结点)

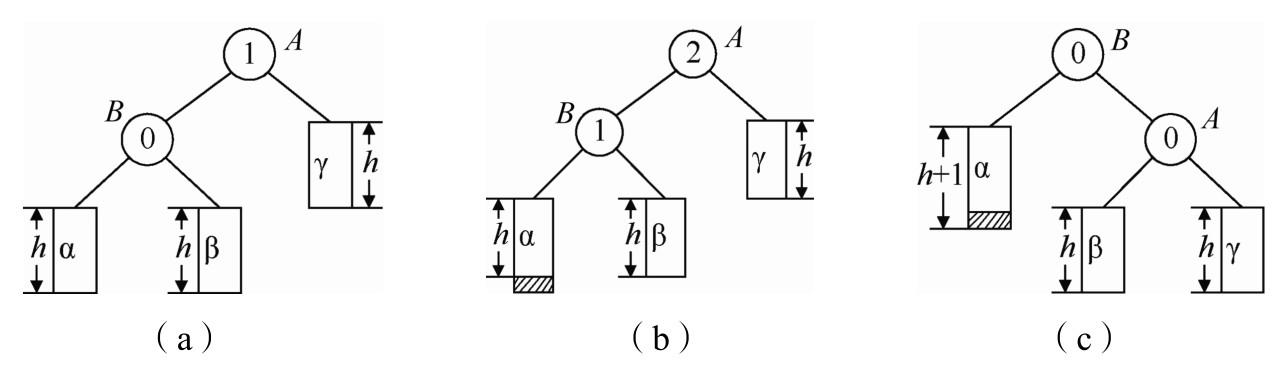
代码如下:

AVLNode *AVLTree::LL_Rotate(AVLNode *a)
{
	AVLNode *b;
	b = a->lchild;
	a->lchild = b->rchild;
	b->rchild = a;
	a->bf = b->bf = 0;
	return b;
}

RR型调整:
(带阴影的小框表示插入的结点)

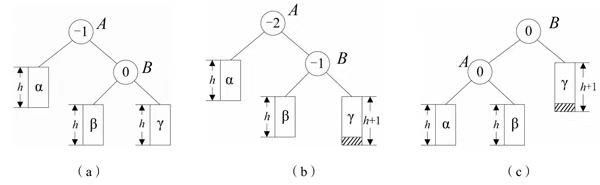
代码如下:

AVLNode *AVLTree::RR_Rotate(AVLNode *a)
{
	AVLNode *b;
	b = a->rchild;
	a->rchild = b->lchild;
	b->lchild = a;
	a->bf = b->bf = 0;
	return b;
}

LR型调整:
(带阴影的小框表示插入的结点)

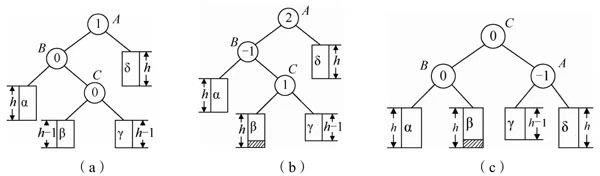
情况一:
(C为新插入的结点)

情况二:
(F为新插入的结点)

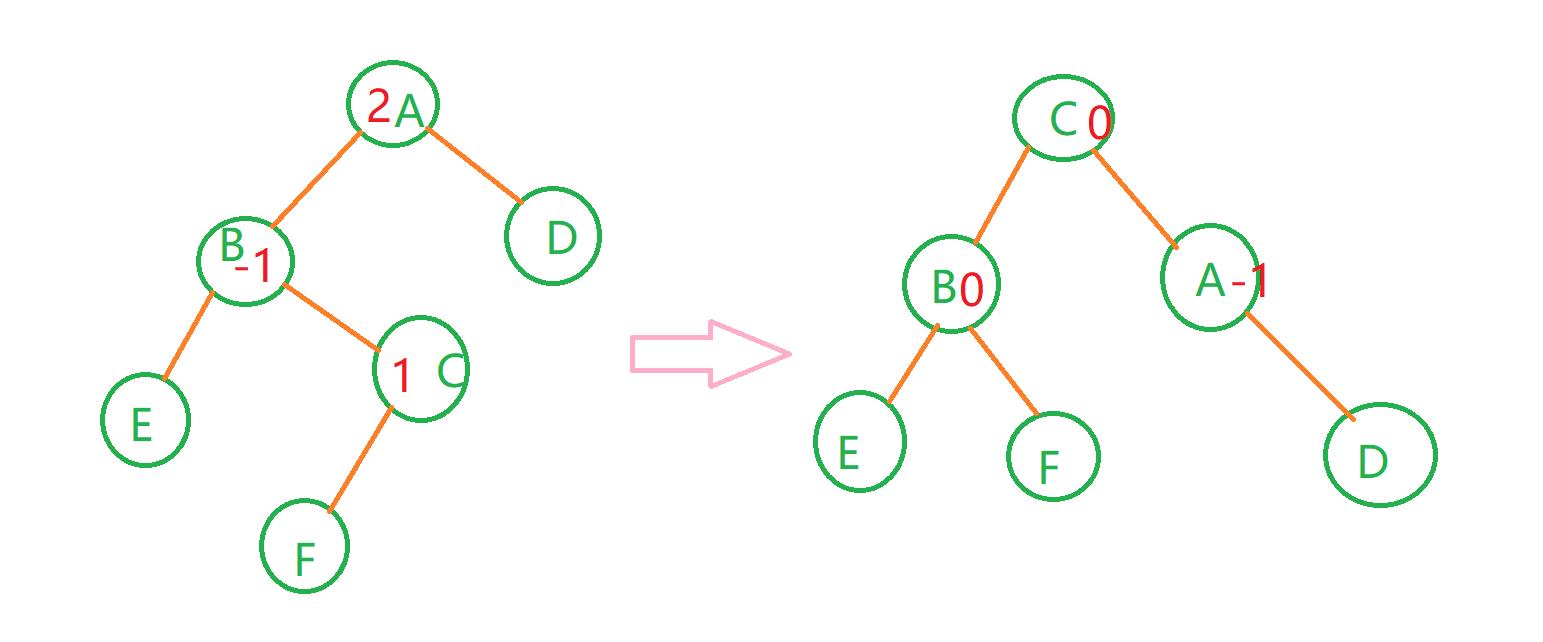
情况三:
(F为新插入的结点)

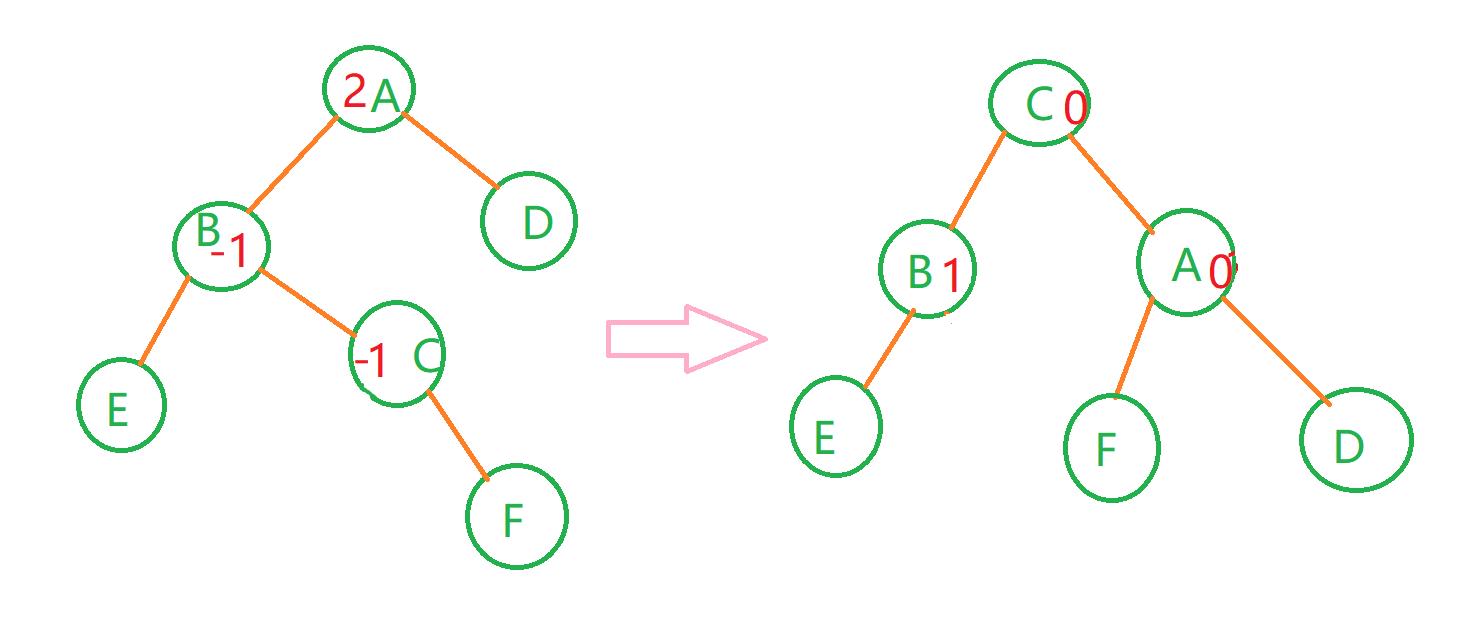
代码如下:

AVLNode *AVLTree::LR_Rotate(AVLNode *a)
{
	AVLNode *b, *c;
	b = a->lchild;
	c = b->rchild;
	a->lchild = c->rchild;
	b->rchild = c->lchild;
	c->lchild = b;
	c->rchild = a;
	if (c->bf == 1)//情况二
	{
		a->bf = -1;
		b->bf = 0;
	}
	else if (c->bf == -1)//情况三
	{
		a->bf = 0;
		b->bf = 1;
	}
	else//情况一
	{
		a->bf = b->bf = 0;
	}
	c->bf = 0;
	return c;
}

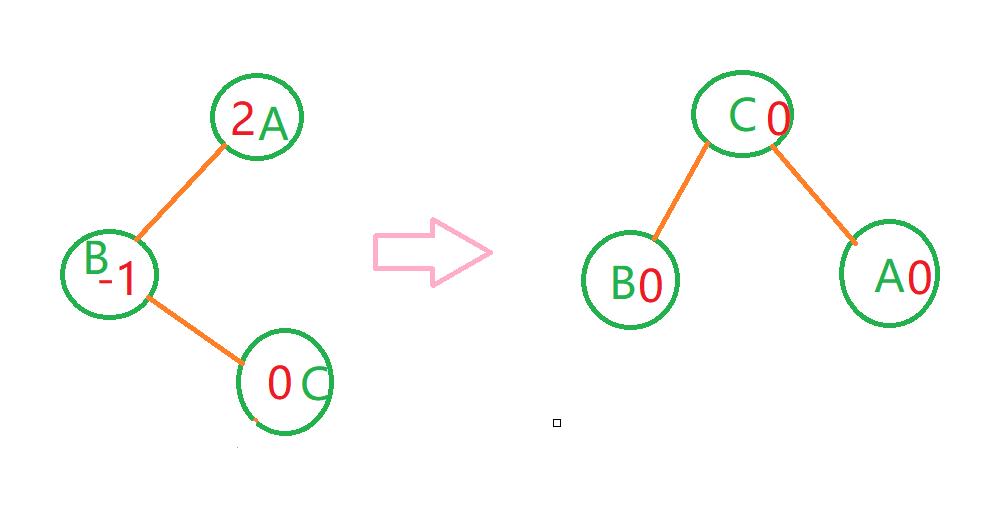
RL型调整:
(带阴影的小框表示插入的结点)

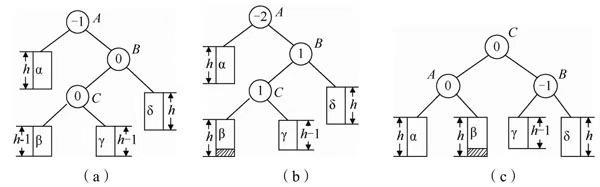
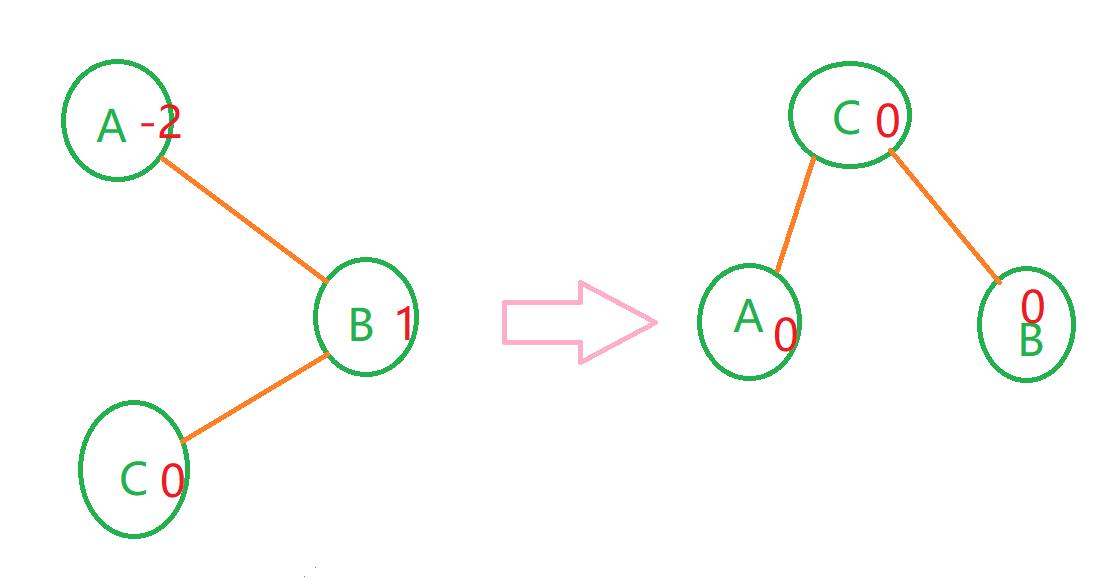
情况一:
(C为新插入的结点)

情况二:
(F为新插入的结点)

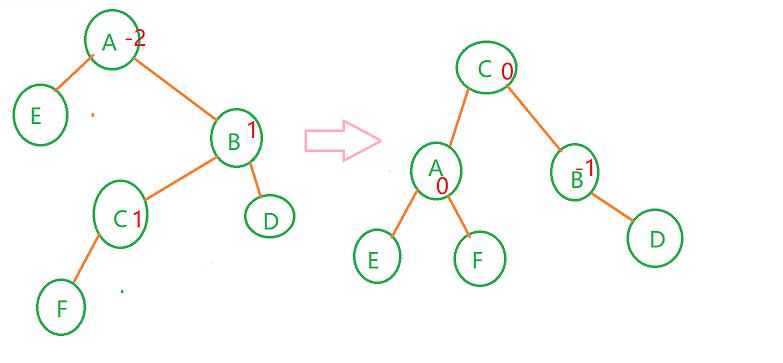
情况三:
(F为新插入的结点)

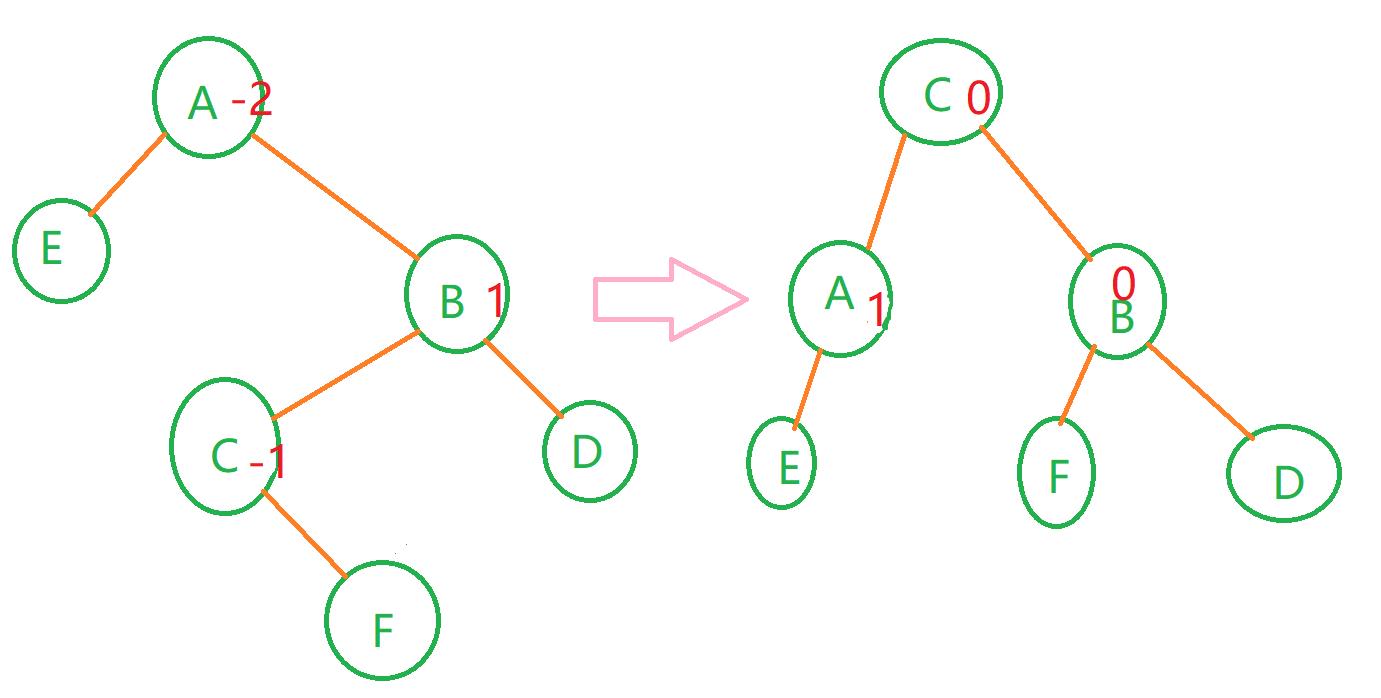
代码如下:

AVLNode *AVLTree::RL_Rotate(AVLNode *a)
{
	AVLNode *b, *c;
	b = a->rchild;
	c = b->lchild;
	a->rchild = c->lchild;
	b->lchild = c->rchild;
	c->lchild = a;
	c->rchild = b;
	if (c->bf == 1)//情况二
	{
		a->bf = 0;
		b->bf = -1;
	}
	else if (c->bf == -1)//情况三
	{
		a->bf = 1;
		b->bf = 0;
	}
	else//情况一
	{
		a->bf = b->bf = 0;
	}
	c->bf = 0;
	return c;
}