三万五千字长文!让你懂透编译原理——第六章 属性文法和语法制导翻译
Posted Leokadia Rothschild
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了三万五千字长文!让你懂透编译原理——第六章 属性文法和语法制导翻译相关的知识,希望对你有一定的参考价值。
三万五千字长文!让你懂透编译原理(六)——第六章 属性文法和语法制导翻译
长文预警
系列文章传送门:
万字长文+独家思维导图!让你懂透编译原理(一)——第一章 引论
万字长文!让你懂透编译原理(二)——第二章 高级语言及其语法描述
近三万字长文!让你懂透编译原理(三)——第三章 词法分析
三万多字长文!让你懂透编译原理(四)——第四章 语法分析—自上而下分析
六万多字长文!让你懂透编译原理(五)——第五章 语法分析—自下而上分析
三万五千字长文!让你懂透编译原理(六)——第六章 属性文法和语法制导翻译
六万字长文!让你懂透编译原理(七)——第七章 语义分析和中间代码产生
文章目录
6.1 属性文法
属性文法(也称属性翻译文法)
-
Knuth在1968年提出
-
以上下文无关文法为基础
-
为每个文法符号(终结符或非终结符)配备若干相关的“值”(称为属性)。
-
属性代表与文法符号相关信息,如类型、值、代码序列、符号表内容等
-
属性可以进行计算和传递
-
语义规则:对于文法的每个产生式都配备了一组属性的计算规则,对属性进行计算和传递。


属性
综合属性:“自下而上”传递信息
继承属性:“自上而下”传递信息

属性文法的说明


语义规则所描述的工作



综合属性

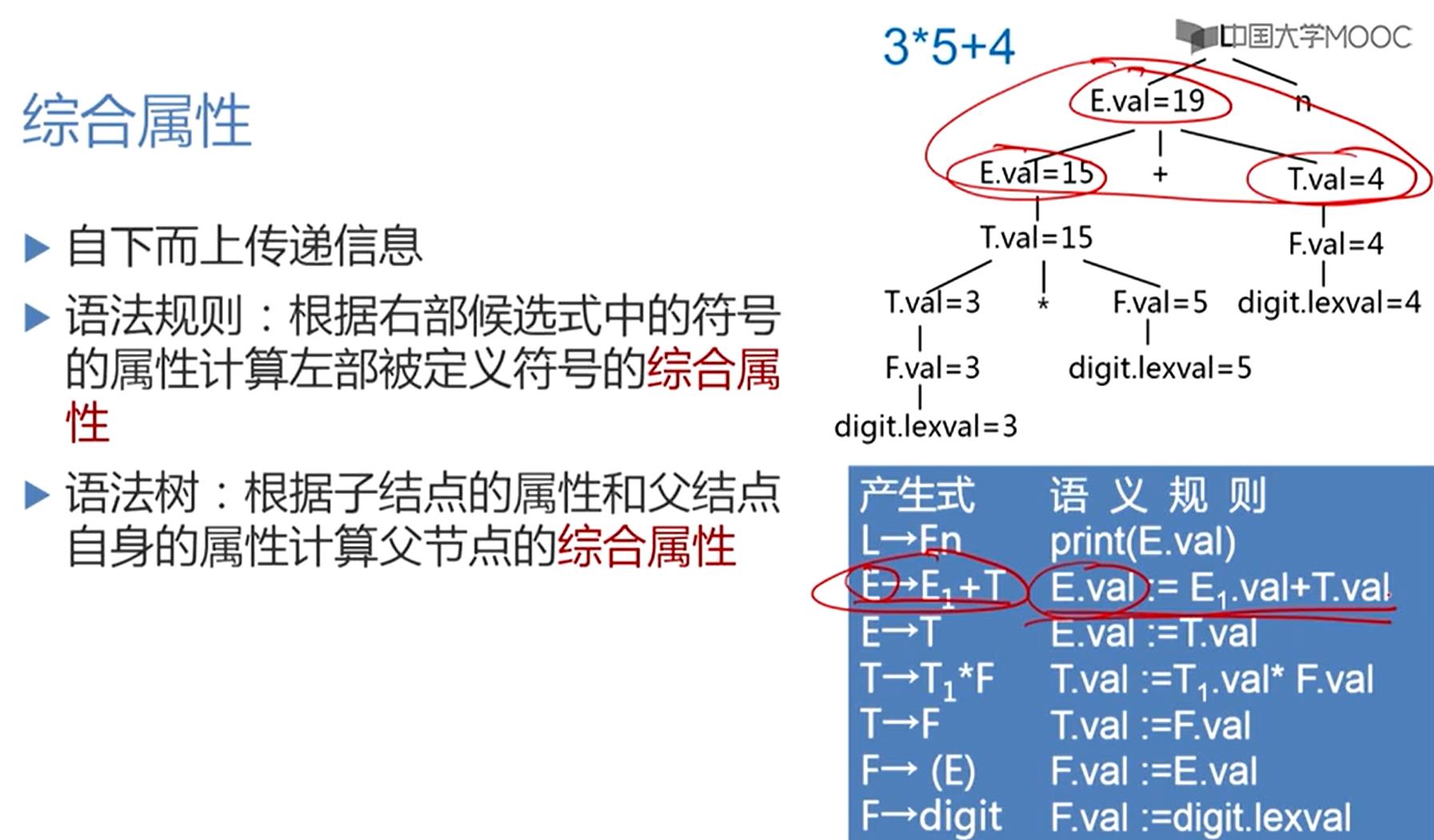
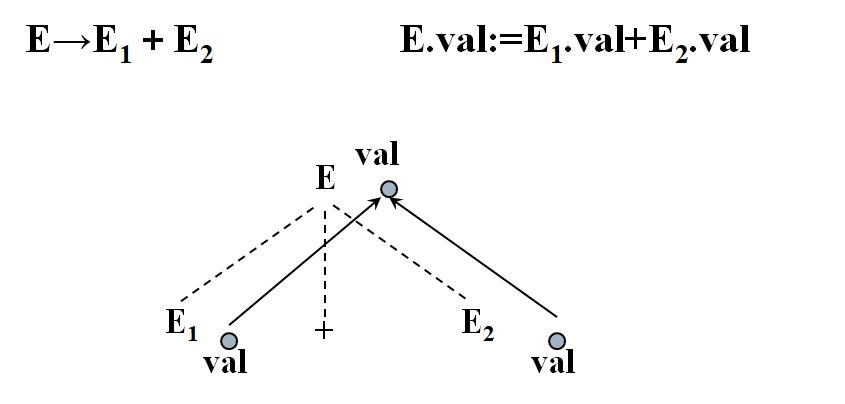
e.g. 对于E→E1+T这条规则,配备的语义规则是:左边的E的val属性是由右部候选当中的E1非终结符和T非终结符的val属性值,两个属性值做加法得到,就是根据右部候选式的符号属性来计算左部被定义的非终结符的综合属性
综合属性主要是用来自下而上的传递语义信息。


继承属性

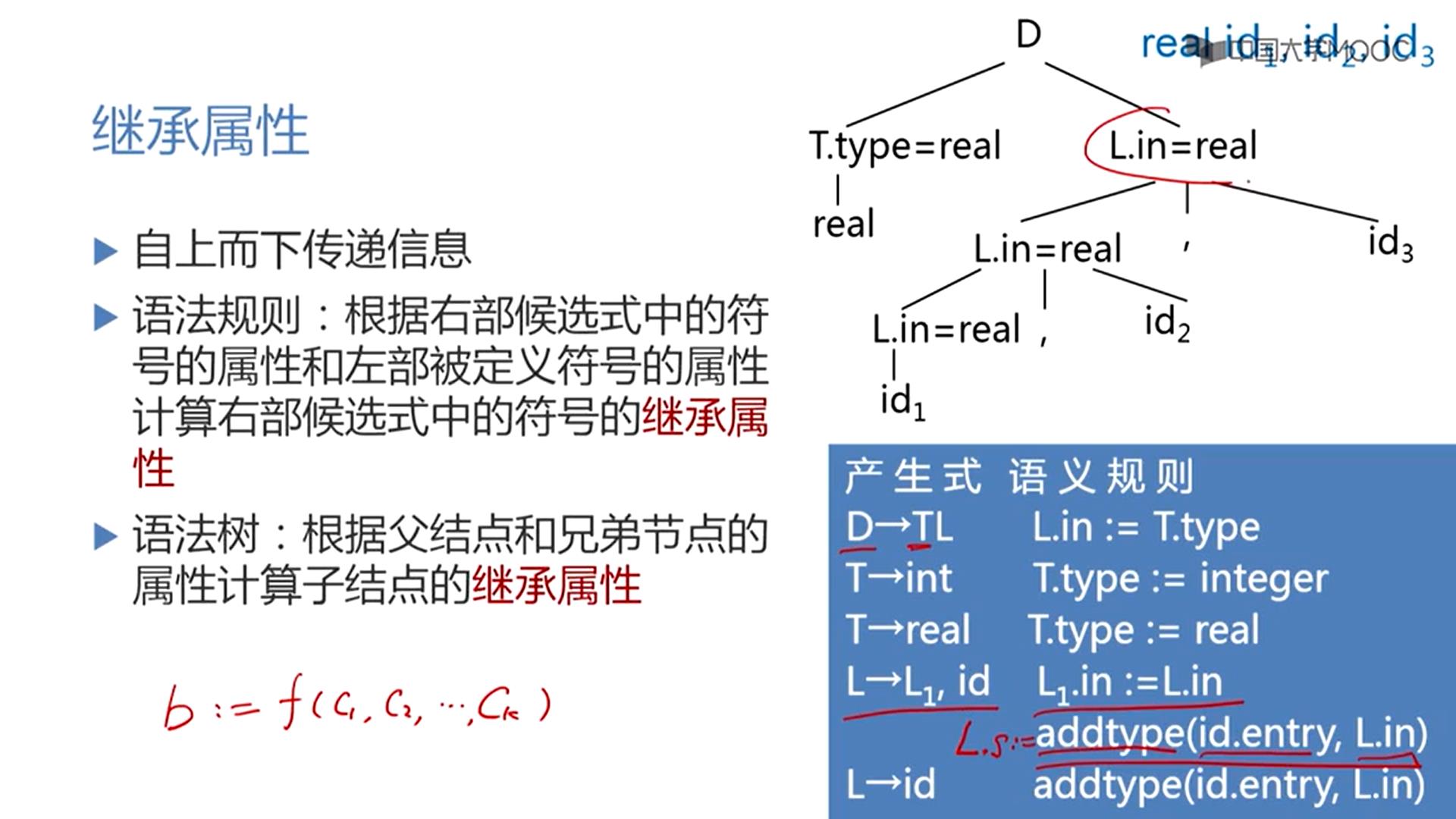
e.g. L→L1.id 对应的语义规则有两条,
其中第一条语义规则说的是右边的L1的继承属性in是由左边的被定义的非终结符L的继承属性得到。
第二条规则,调用了addtype这个函数/过程,这个函数/过程的功能,是实现在符号表中,找到id所对应的入口,并且把这个入口当中的类型信息设置为L.in的参数的值,这条规则看上去跟其他规则不同,因为他并没有给某个属性定值,比如其他的规则都是根据某些属性的值设置某些属性的值,而这个addtype没有返回结果,也没有把返回结果给某个属性,这个地方为了统一说法,我们可以认为左部L这个被定义的终结符,有一个虚拟的属性s用来接受addtype的返回结果,这样一来,所有的语义规则都可以写成这种形式:对某些属性进行f函数变换,把变换的结果设置为某些属性的值:
b:=f(c1,c2,…,ck)
对于语法树:右边L.in=real是根据兄弟节点T.type=real计算出来。


属性依赖

E→E1+T这条规则
左边的E的属性依赖于右边的E1和T的综合属性
D→TL
L的继承属性是根据左边的兄弟节点T计算得到,所以L.in是T的计算结果,是T的type属性,右部L的继承属性是依赖于它的兄弟节点,也是产生式右部的某个符号的属性
L→L1,id
这条语法规则,他有两条语义规则,右边的L1的继承属性是根据左边的L继承属性得到,右边的L1的继承属性依赖于左边的L继承属性
Ls=addtype(id.entry,L.in),虚拟的Ls依赖于id和L的继承属性(id.entry,L.in)


第一点
D→TL对应的语义规则应该说明,右边的TL这些符号的继承属性怎么算,或者是左边的这个符号的综合属性怎么算,该例说明了左边的这个符号的综合属性怎么算
对于E→E1+T这条规则,对应的语义规则应该说明,左边的这个符号的综合属性怎么算,或者说右边的E1和T如果有继承属性的话,也应该说明这些符号的继承属性怎么算,由于该例E1和T没有有继承属性,所以只要说明左边的E的综合属性怎么算,这条规则说明左边E的综合属性是由右边符号相加得到
第二点
L→id 应该说明L的综合属性怎么算(如果L有综合属性的话)
如果涉及到L的继承属性,比如说它所对应的addtype引用了L.in,这里只能引用左边符号的继承属性,而不能说L是怎么算的,因为L的继承属性是依赖于它的兄弟节点和父节点,光看这个产生式,并不知道L的兄弟节点父节点是什么,所以说这个产生式所对应的规则只能使用L的继承属性,而不能说明L的继承属性怎么算,而L的继承属性怎么来,应该由其他产生式得到(e.g.D→TL说明L的继承属性怎么算)

C选项的规则是对B的综合属性做计算,对于出现在产生式右边的符号的综合属性的计算,不应该由这个产生式的规则来介绍,来表述,因为B的综合属性是依赖于它的子节点,而A→BC根本看不到B的子节点所对应的文法符号,所以B的综合属性不能在这个产生式的语义规则里面给出来怎么算。
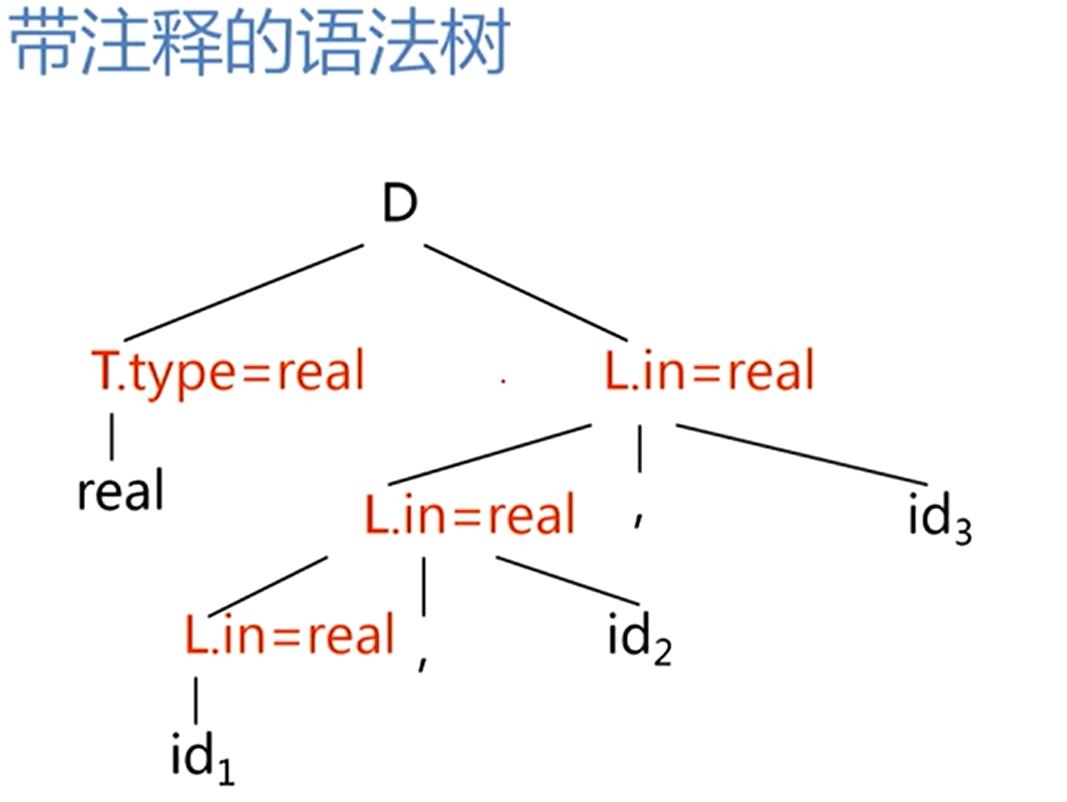
带注释的语法树
对语法树进行拓广

S-属性文法只有综合属性,所以可以把语法树的构造过程和属性的计算过程合并,一遍自下而上进行语法分析构造语法树,一遍计算每个新构造出来节点的综合属性,这样,当把整个语法树都构造完了后,每个节点的综合属性也就计算完了。
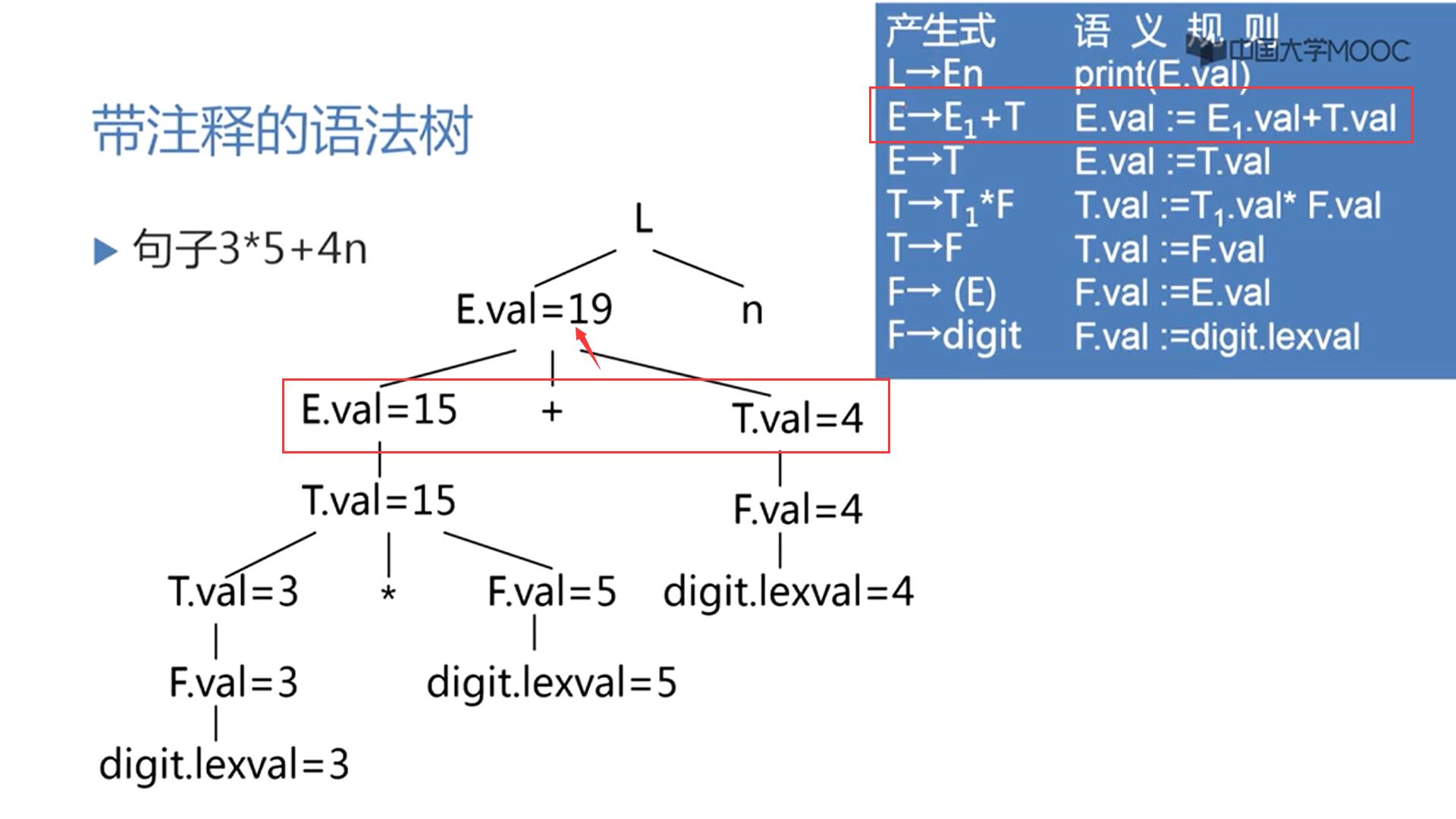
用哪个产生式做归约,就用对应的语义规则,就可以得到对应父节点的综合属性值

如果既有综合属性,又有继承属性,不是一个S-属性文法
我们不能够把语法树的构造过程和属性的计算过程合并
第二条规则,调用了addtype这个函数/过程,这个函数/过程的功能,是实现在符号表中,找到id所对应的入口,并且把这个入口当中的类型信息设置为L.in的参数的值,因此我们也要看符号表的变化
先看子树T-real,用第三条规则
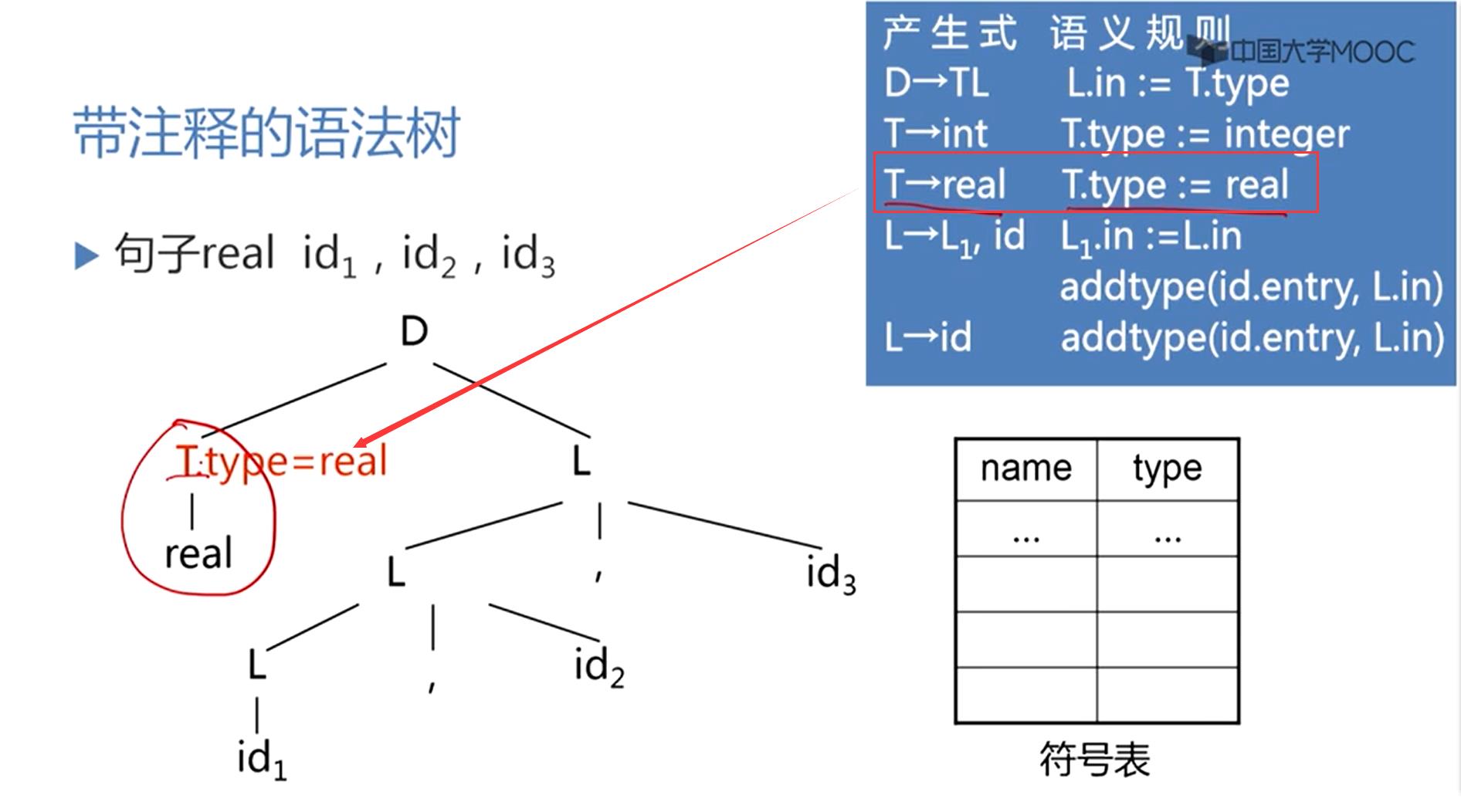
L的继承属性应该根据兄弟节点T的继承属性来计算
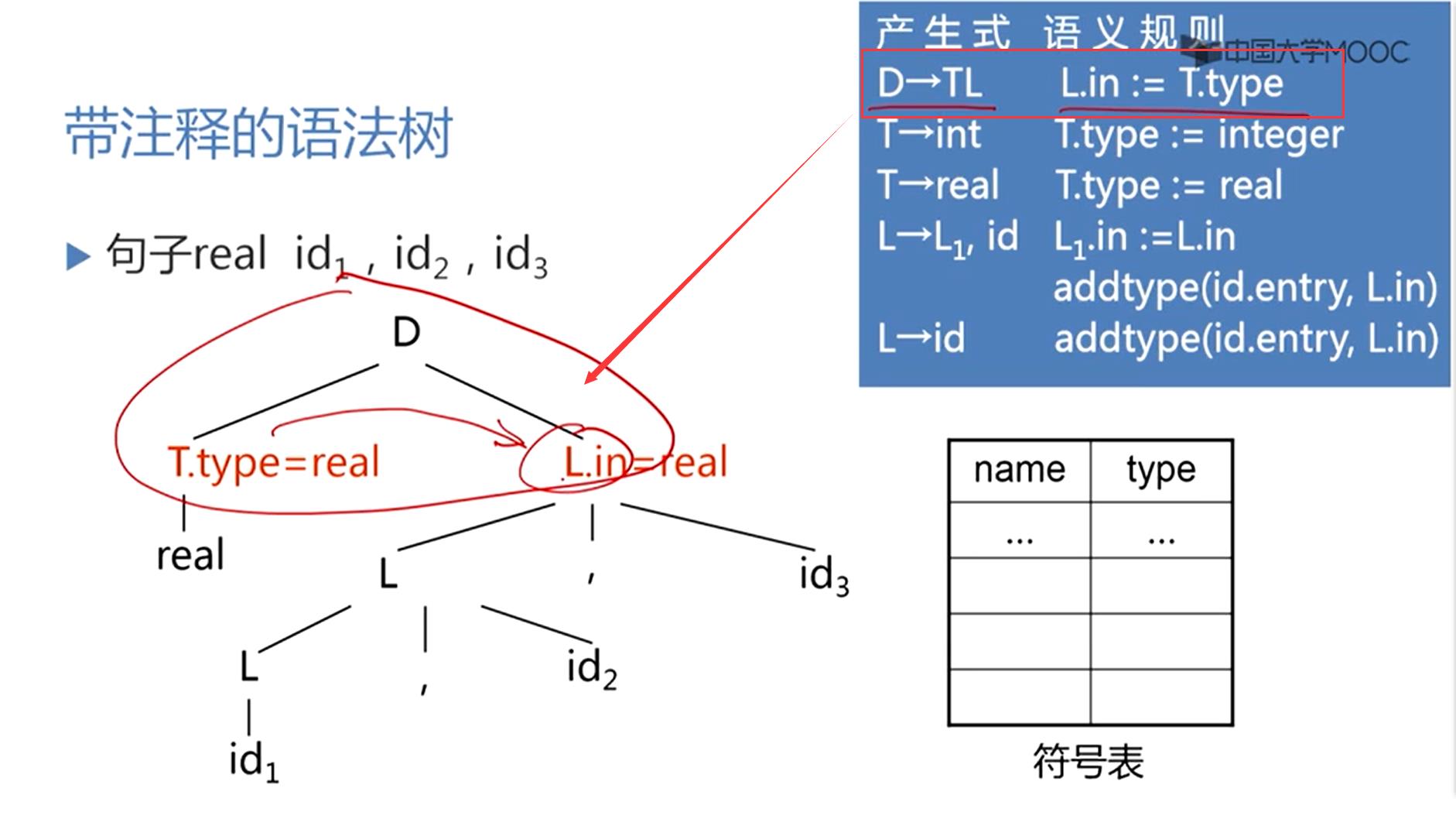
对于第三个子树,用第四个产生式
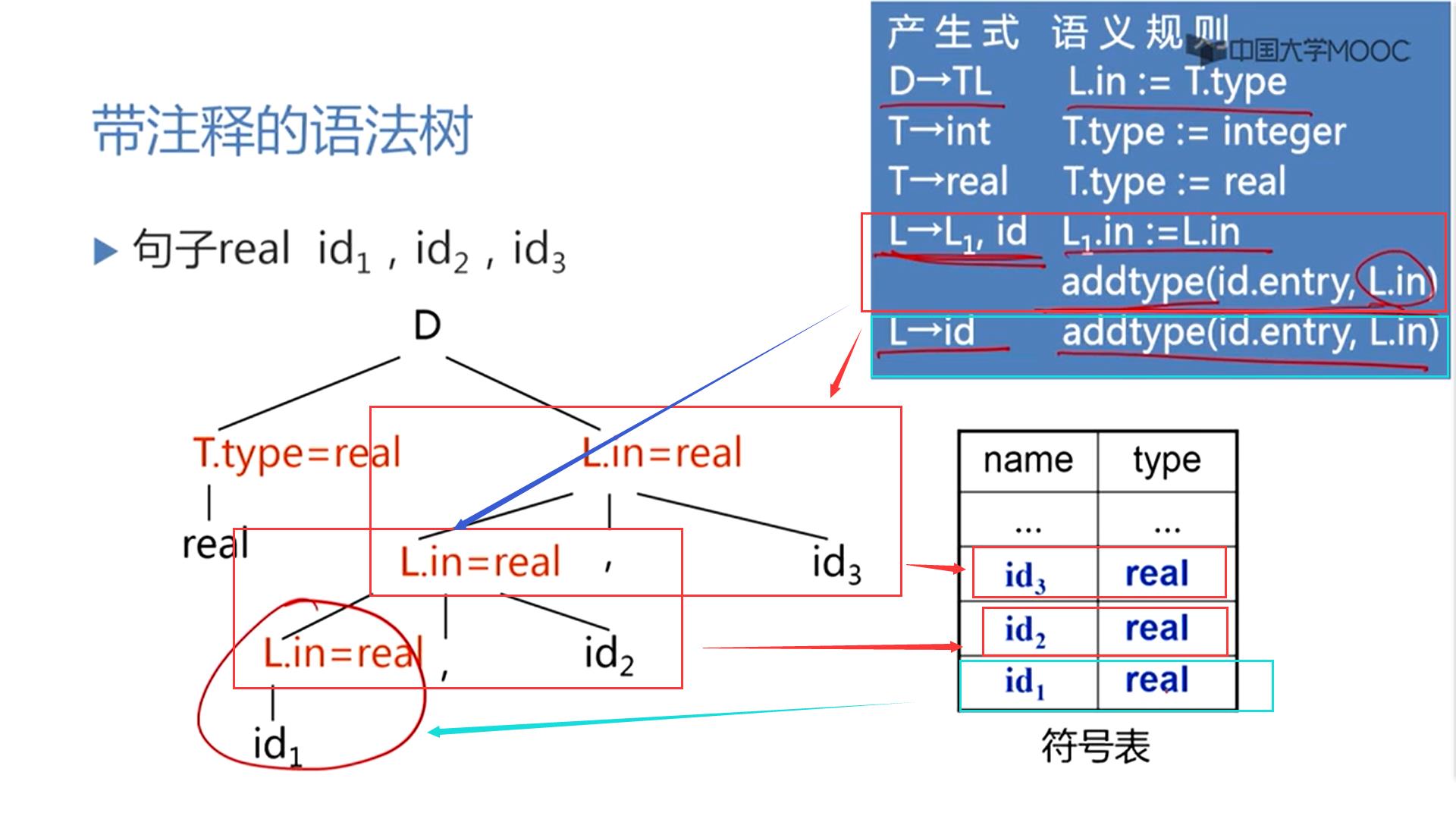
第一个语义规则说L的继承属性由父节点传过来
第二个addtype这个函数/过程,这个函数/过程的功能,是实现在符号表中,找到id所对应的入口,并且把这个入口当中的类型信息设置为L.in的参数的值real
6.2 基于属性文法的的处理方法



6.2.1 依赖图



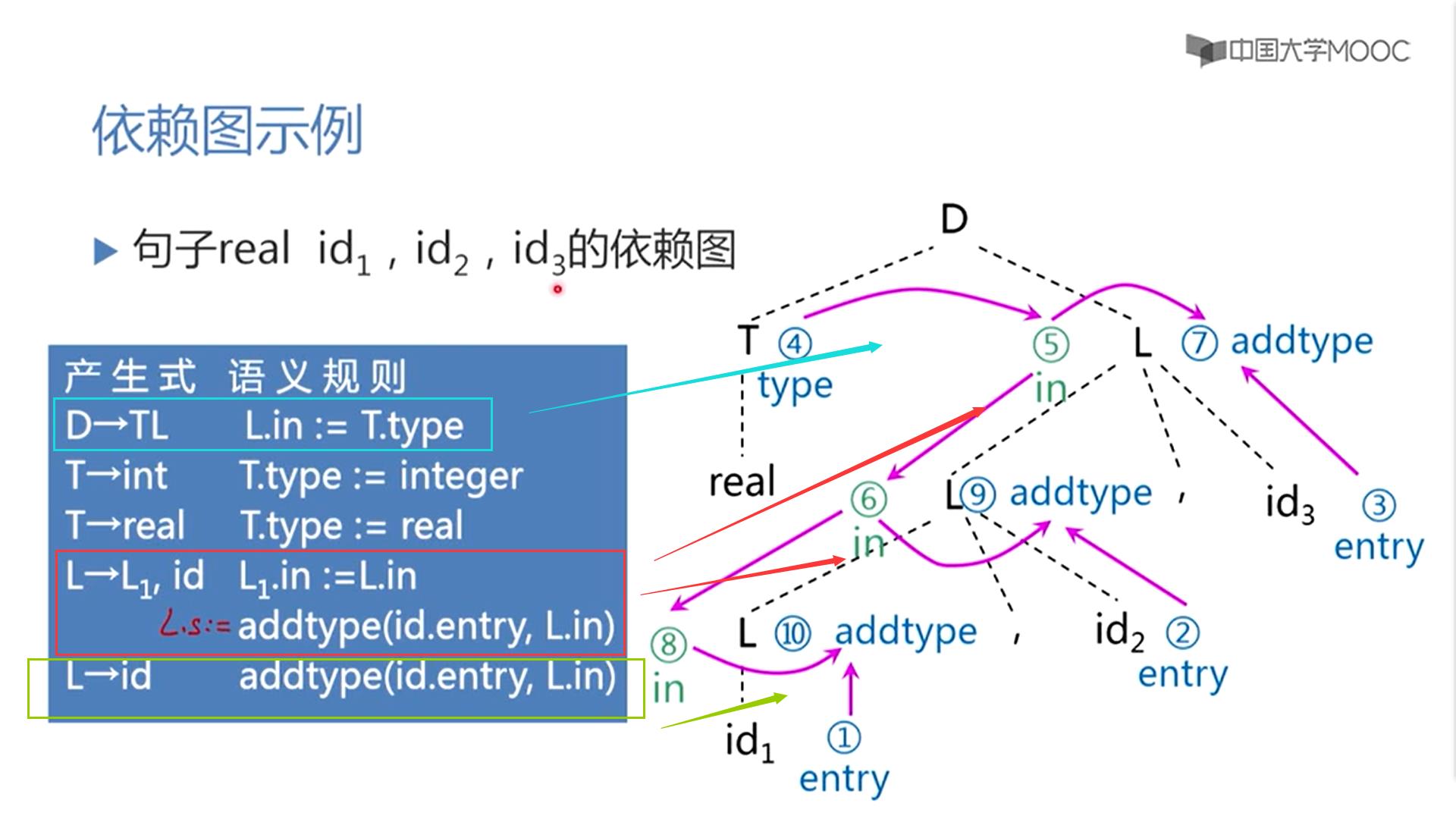
先将所有节点对应的属性标出来
1,2,3→三个非终结符对应的节点
7,9,10对于第四条产生式第二个规则假设L有个虚拟的属性L.s来接受,所以虚拟的也有个节点
按照每个节点构成时所对应的产生式对应的每一条语义规则,画出语义规则表达的属性之间的依赖边
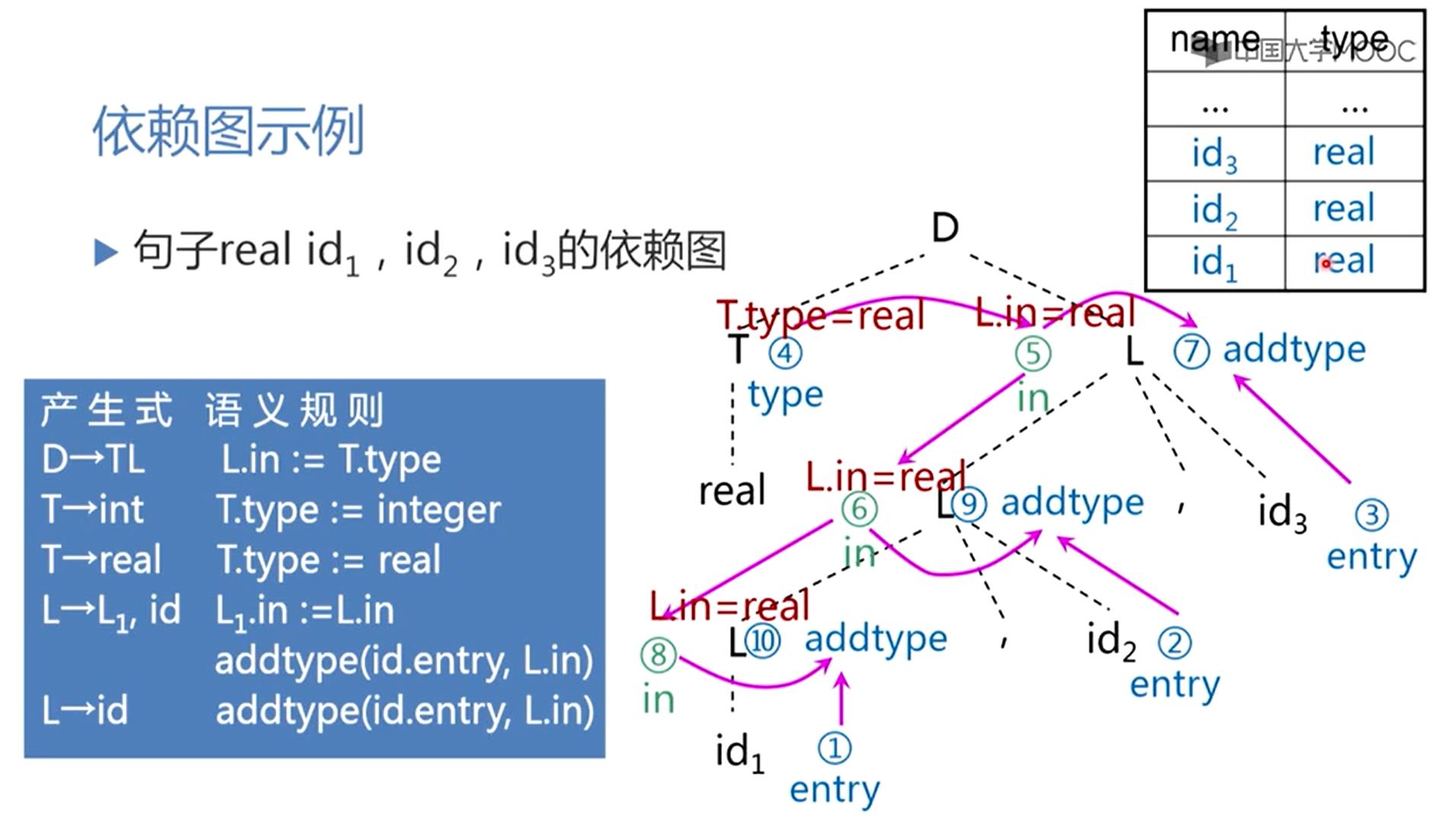
如果一属性文法不存在属性之间的循环依赖关系,那么称该文法为良定义的
属性的计算次序
- 一个依赖图的任何拓扑排序都给出一个语法树中结点的语义规则计算的有效顺序
- 属性文法说明的翻译是很精确的

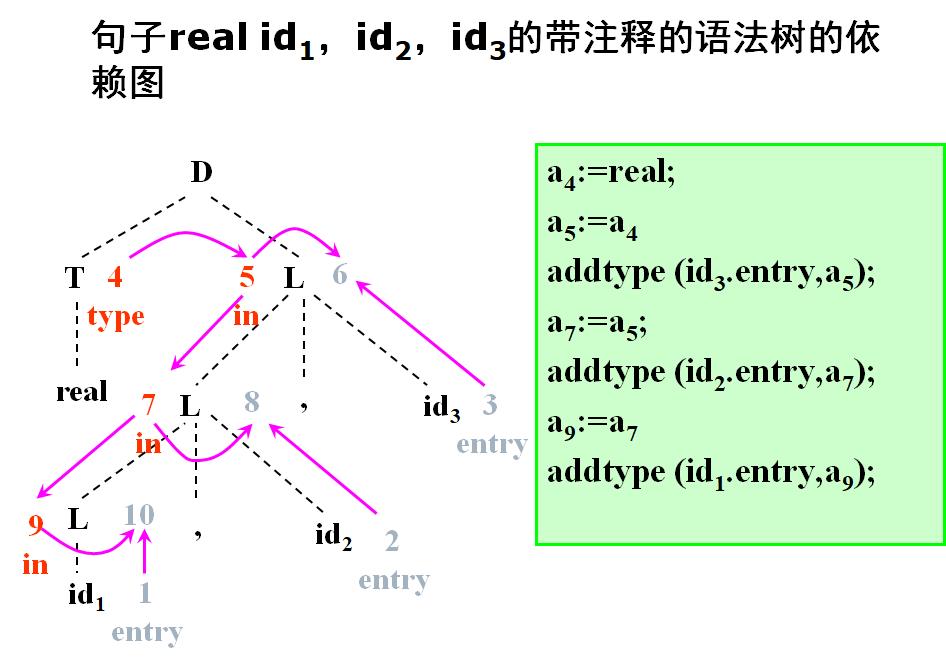
6.2.2 树遍历

While 还有未被计算的属性 do
VisitNode(S) /*S是开始符号*/
如果属性文法是良定义的,通过反复遍历,一定能够把所有的文法都计算出来
procedure VisitNode (N:Node) ;
begin
if N是一个非终结符 then
/*假设它的产生式为N→X1…Xm*/
for i :=1 to m do
if Xi∈VN then /*即Xi是非终结符*/
begin
计算Xi的所有能够计算的继承属性;
VisitNode (Xi)
end;
计算N的所有能够计算的综合属性
end
VisitNode功能:对已输入参数的子数,进行从左到右深度优先遍历,依次考察每个节点,把能够计算的节点计算出来

蓝色代码:对输入参数N进行检查,如果N是个非终结符的话,就按照树,对以N为根的子树进行深度优先,从左到右的遍历,把所有的属性计算出来(通过递归调用来实现的,对每个子节点调VisitNode)
注意:在递归调用每一个子节点之前,先把每一个子节点对应的继承属性计算出来
当X1,X2,X3…的属性都计算完了,就可以计算N的综合属性了
树遍历算法示例

首先对输入串的语法分析,建立该输入串的语法树
我们知道,作为文法的开始符号,如果有继承属性的话,继承属性的值应该作为属性计算的初始值
所以假设S有一个继承属性S.a设为0,开始用树遍历的算法进行工作:
主程序总是调用VIsitNodeS,对以S为根的子树进行一遍,一遍的遍历,知道所有的属性都计算出来。
第一次调用VIsitNodeS,S是一个非终结符,
用产生式S→XYZ
因此,对XYZ三棵子树调用VisitNode
首先,在调用VIsitNodeX之前,应该把X的继承属性能算的先算出来
对于以X为根的子树,他有一条语义规则,说的是:X的继承属性c依赖于Z的属性g,由于Z的属性现在还没出来,所以X的继承属性c没法算,因此直接调VisitNode(X)
VisitNode(X)发现子节点是个终结符x,用到规则X→x,x没有继承属性要算,也不需要递归,直接处理完了,那么就该处理X的综合属性,按照这条规则,这个子树所对应的规则X.d=2*X.c,X.c现在没有出来,X.d没法算,X处理完了,没得到什么属性
回到VisitNodeS里面,接着处理Y,在VisitNodeY之前首先计算Y能计算的继承属性,根据S为根的子树Y.e=S.b
S.b没出来,Y的继承属性没法算,直接调VIsitNodeY,进入VisitNodeY发现子节点y是个终结符,不需要再递归,也没有属性要计算,就要针对这个子树,建立y的综合属性的算法,但Y.e没出来,Y的综合属性f没法算,这个树上也没有增长什么属性,到了VisitNodeZ
VisitNodeZ之前,应该把所有Z的继承属性能算的先算出来,按照以S为根的这条子树,它所对应的规则,Z.h=S.a=0,这就是Z能算的继承属性,算了Z能算的继承属性之后,得VisitNode(Z)
遍历以Z为根所对应的子树,子节点是终结符,没有属性要算,就得处理Z综合属性,Z.g=Z.h+1=1
将Z两个属性都算完了
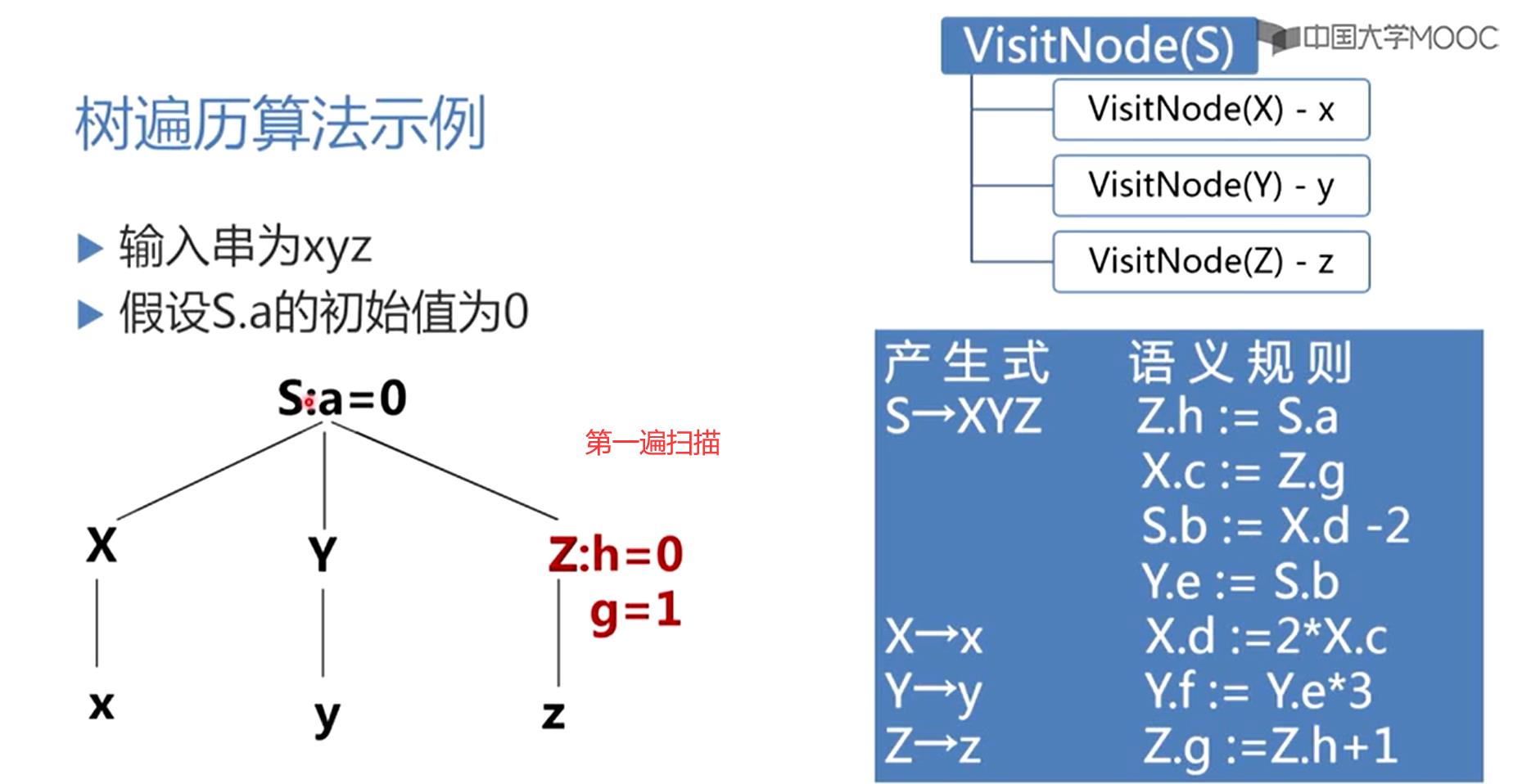
VisitNodeZ处理完了,第一次调用VisitNodeS就完了,注意,在VisitNodeS结束之前,最后一个动作是把所有的子节点都处理完了之后,应该要计算父节点的综合属性,这个综合属性有一条规则,S.b=X.d-2,所依赖的X.d现在还没有,所以S的综合属性现在还不能算
由于还有属性没算,主程序还会调一次VisitNodeS
第二次调用VisitNodeX,依次遍历它的每一个子树,在调用VIsitNodeX之前,应该把X的继承属性能算的先算出来,对于以X为根的子树,他有一条语义规则,说的是:X的继承属性c依赖于Z的属性g,X.c=Z.g=1,算完能算的继承属性之后,再VisitNodeX
VisitNode(X)发现子节点是个终结符x,用到规则X→x,x没有继承属性要算,也不需要递归,直接处理完了,那么就该处理父节点X的综合属性,按照这条规则,这个子树所对应的规则X.d=2*X.c=2,X处理完了。
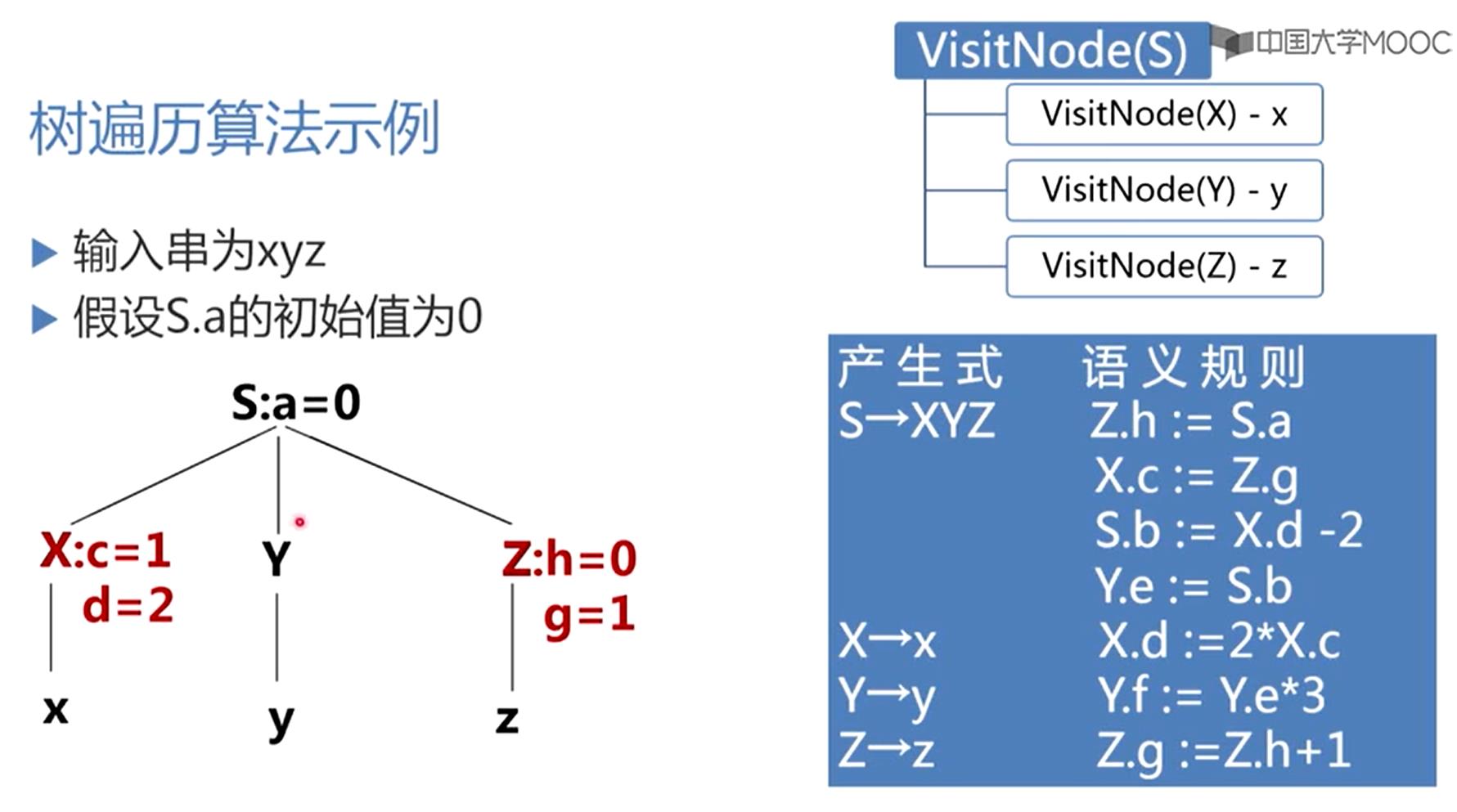
下面VisitNodeY,在VisitNodeY之前首先计算Y能计算的继承属性,根据S为根的子树Y.e=S.b
S.b没出来,Y的继承属性没法算,直接调VIsitNodeY,进入VisitNodeY发现子节点y是个终结符,不需要再递归,也没有属性要计算,就要针对这个子树,建立y的综合属性的算法,但Y.e没出来,Y的综合属性f没法算,这个树上也没有增长什么属性,到了VisitNodeZ
下面再VisitNodeZ,因为这个属性刚刚都算完了,很快跳过,当VisitNodeZ完了后
对于VIsitNodeS,XYZ处理完了,应该处理S的综合属性,S.b=X.d-2=0,S的第二遍调用完毕
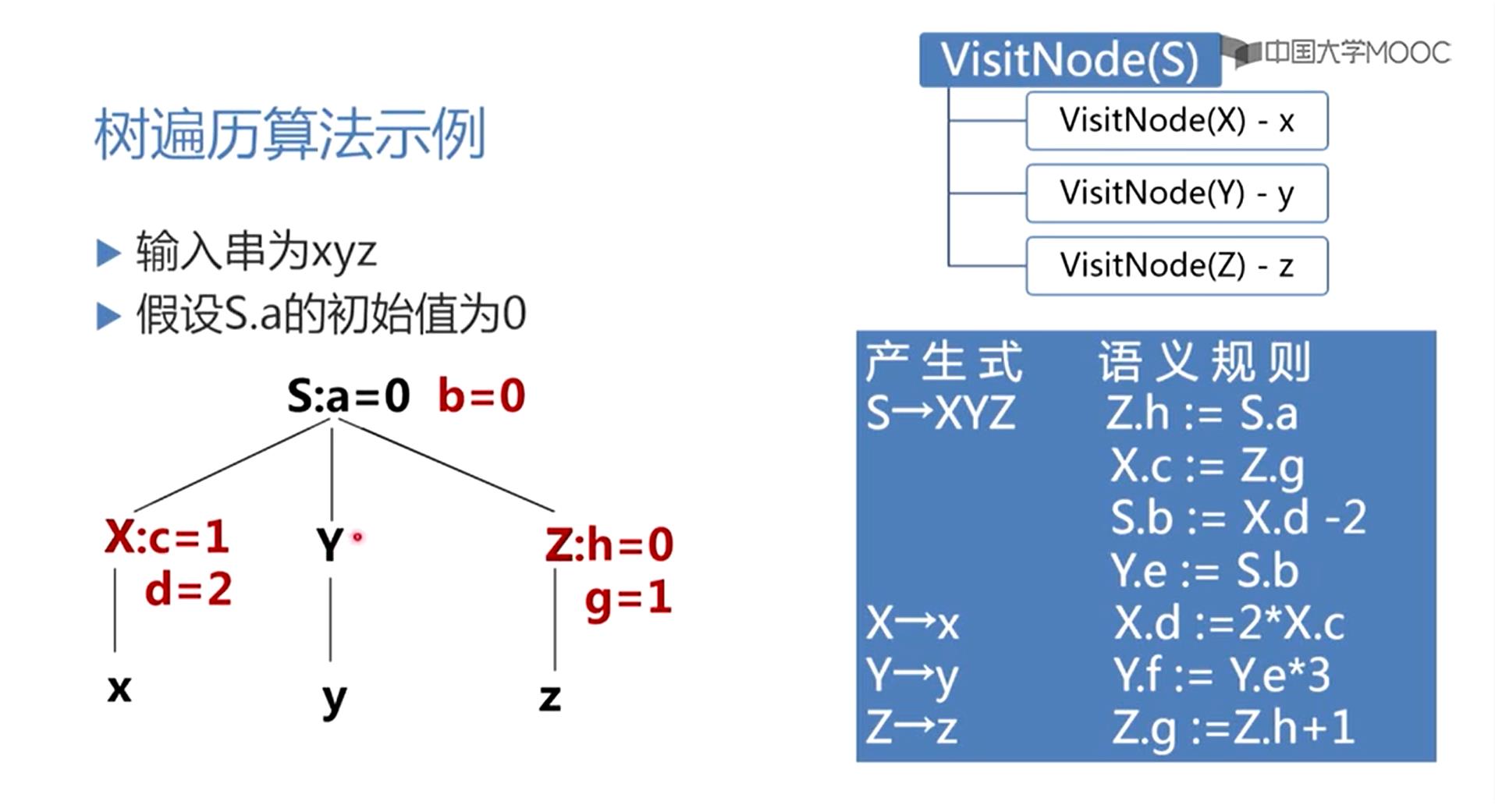
由于还是有未被计算的属性,再次进行第三次调用VisitNodeS
由于X属性计算完了,很快调用一遍VisitNodeX,没有变化,再调用VisitNodeY
在VisitNodeY之前首先计算Y能计算的继承属性,根据S为根的子树Y.e=S.b=0
调VIsitNodeY,进入VisitNodeY发现子节点y是个终结符,不需要再递归,也没有属性要计算,就要针对这个子树,建立y的综合属性的算法,Y.f=Y.e*3=0,到了VisitNodeZ

VisitNodeZ之前Z所有属性都处理完了,很快调用结束,然后回到VisitNodeS,S的综合属性也被计算完了,且整个程序没有未被计算的属性,因此程序停止。
6.2.3 一遍扫描的处理方法

L-属性文法适合于一遍扫描的自上而下分析
S-属性文法适合于一遍扫描的自下而上分析
6.2.4 抽象语法树
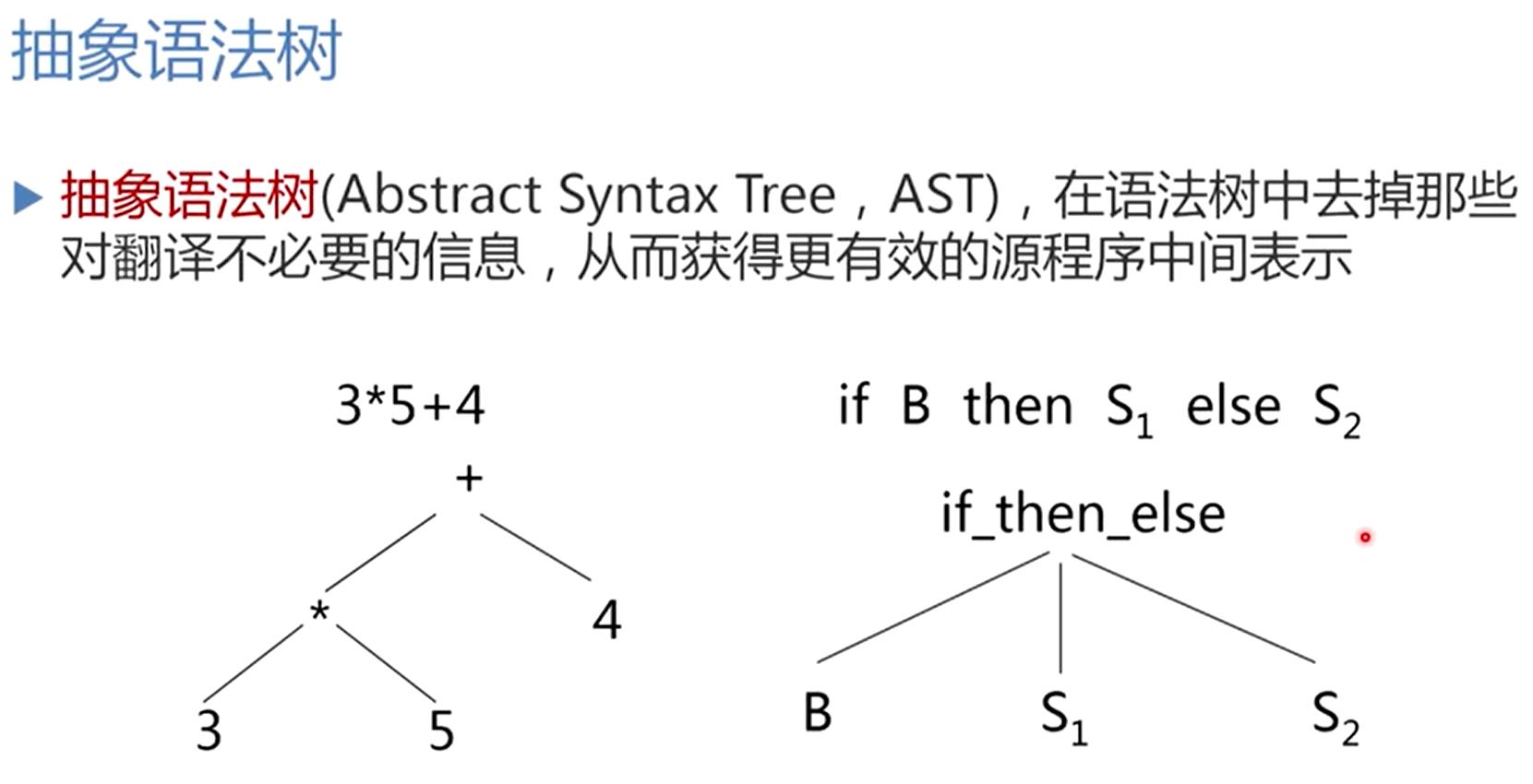

X.nptr指向节点(子树)的指针


a识别为标识符id,自下而上语法分析器id归约成T(属性计算与自下而上分析器结合在一起了)
id归约成T对应的规则说的是
T.nptr := mknode( id, id.entry ) 创建一个叶节点,标记是id,第二个域里面是指向a的入口,而且叶节点由T.nptr指向,自下而上分析符号栈里面现在有T

把T规约为E,T归约成E对应的规则说的是
E.nptr := T.nptr 应该把E.nptr指向T.nptr,所以E.nptr的属性值指向同一个节点,然后移进 - ,把4识别为num
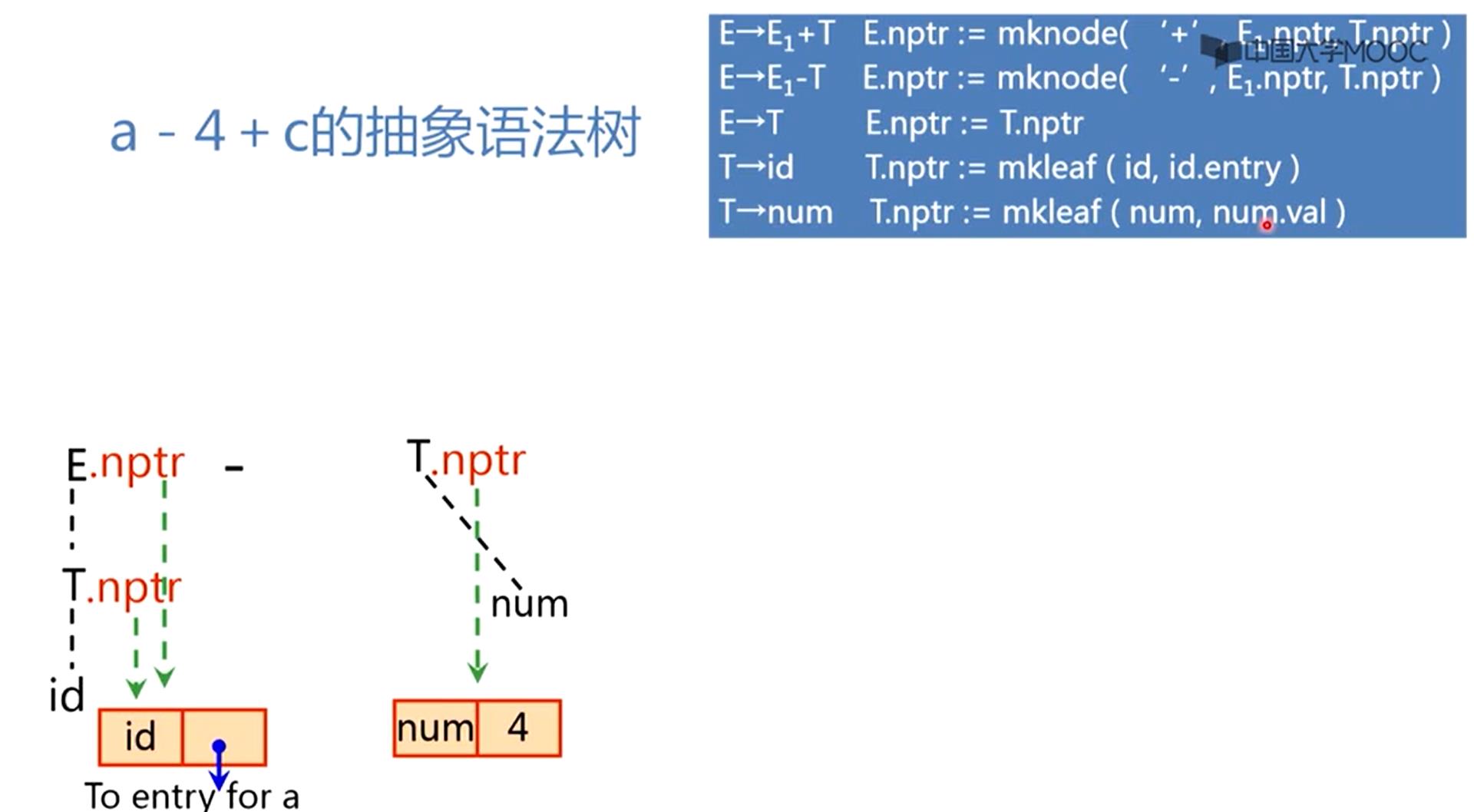
num归约成T,T.nptr := mknode( num, num.val )
为num创造一个叶节点,由T.nptr指向它
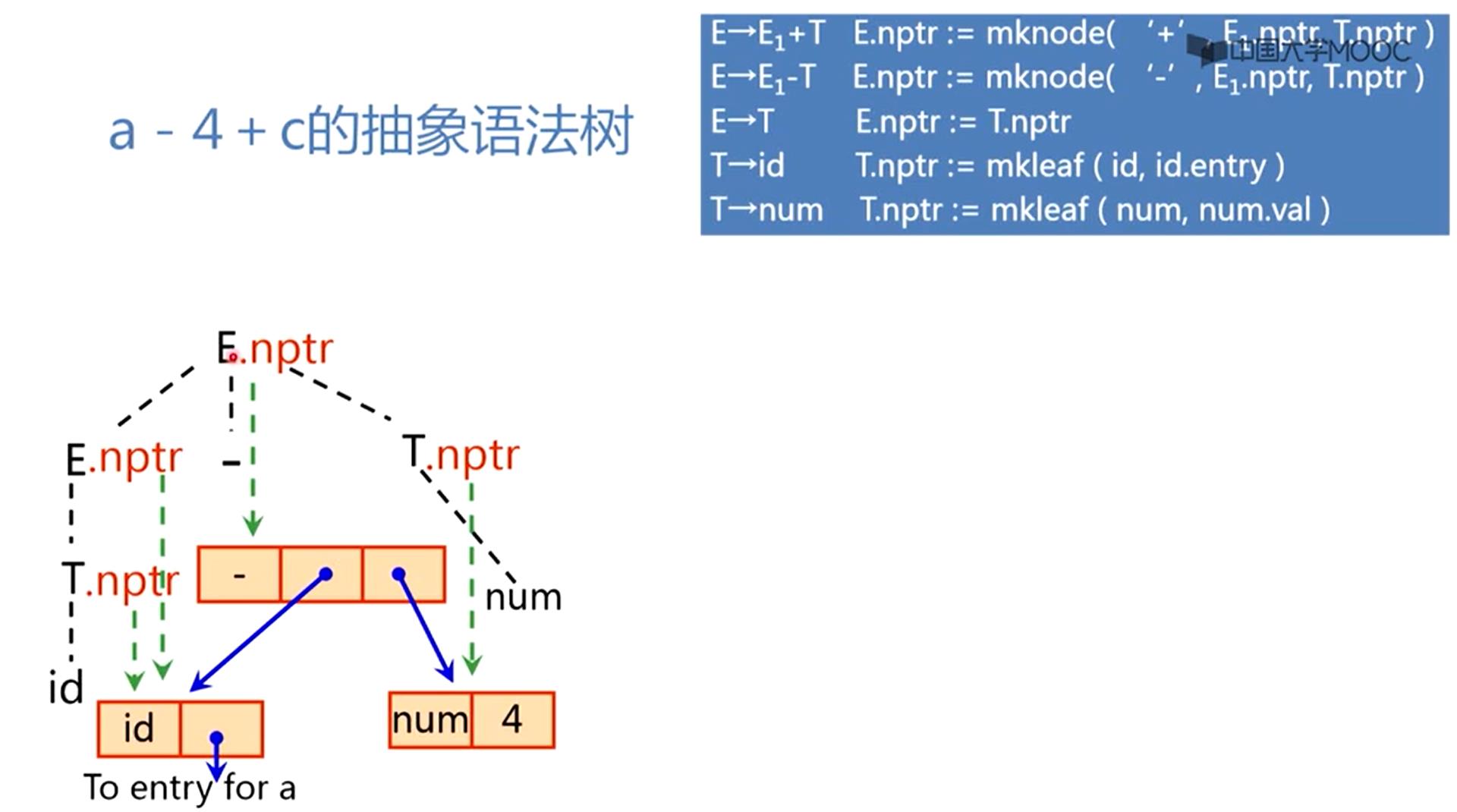
现在栈里面有E-T三个符号,语法分析告诉你要把它归约到E,用第二个产生式做归约,当你用第二个产生式做归约的时候,就得执行相应的语义动作,就得执行相应的语义规则
E→E1-T E.nptr := mknode( ‘-’, E1.nptr, T.nptr )
创建一个-节点,左边指向左子树E1.nptr指向的这个节点,右边指向右子树T.nptr指向的这个节点,同时这个减法节点由新归约后的E.nptr来指向,现在符号栈里面只有E了
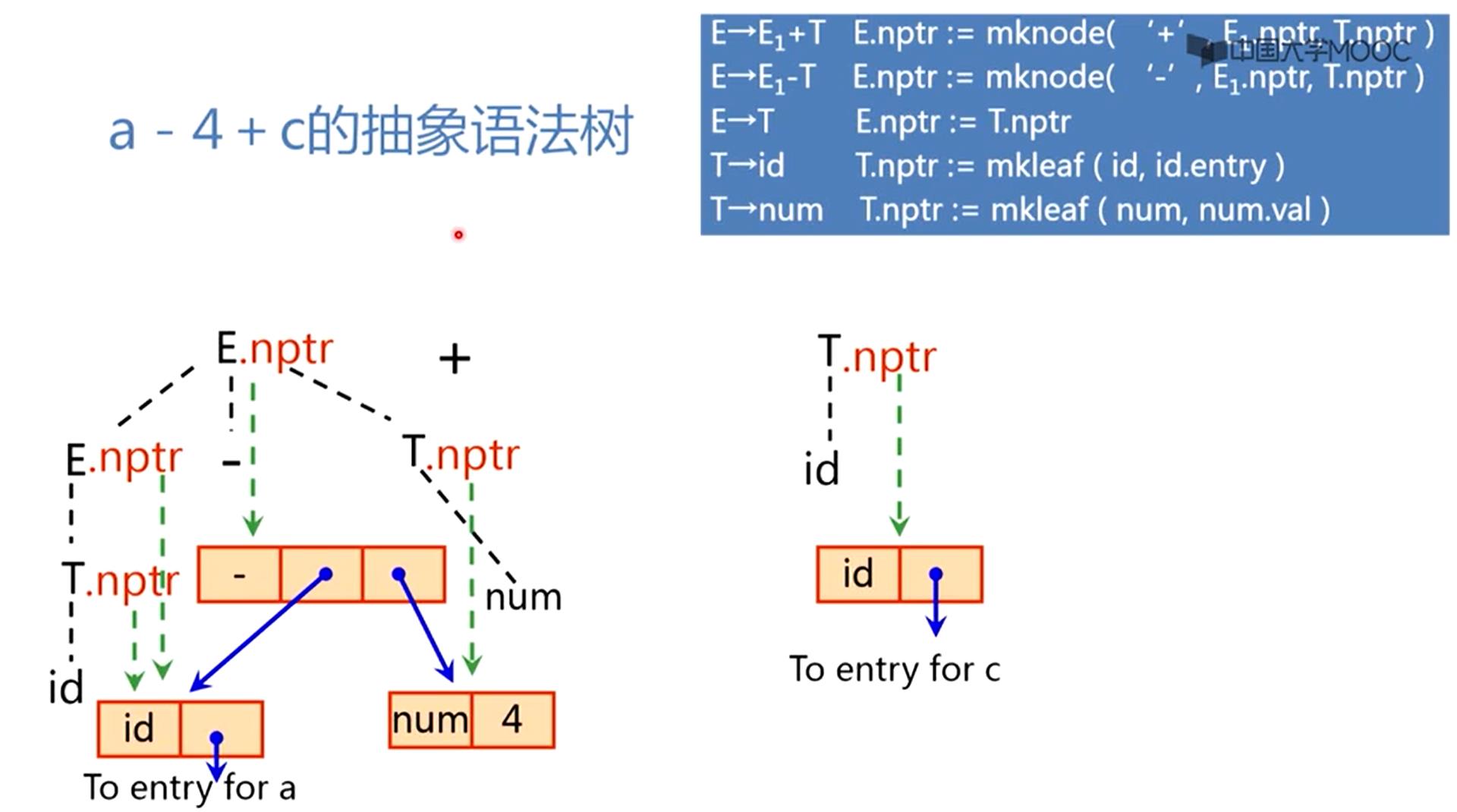
将+移进,把c识别为id,将id规约为T,id归约成T对应的规则说的是
T.nptr := mknode( id, id.entry ) 创建一个叶节点,标记是id,第二个域里面是指向a的入口,而且叶节点由T.nptr指向,自下而上分析符号栈里面现在有E+T
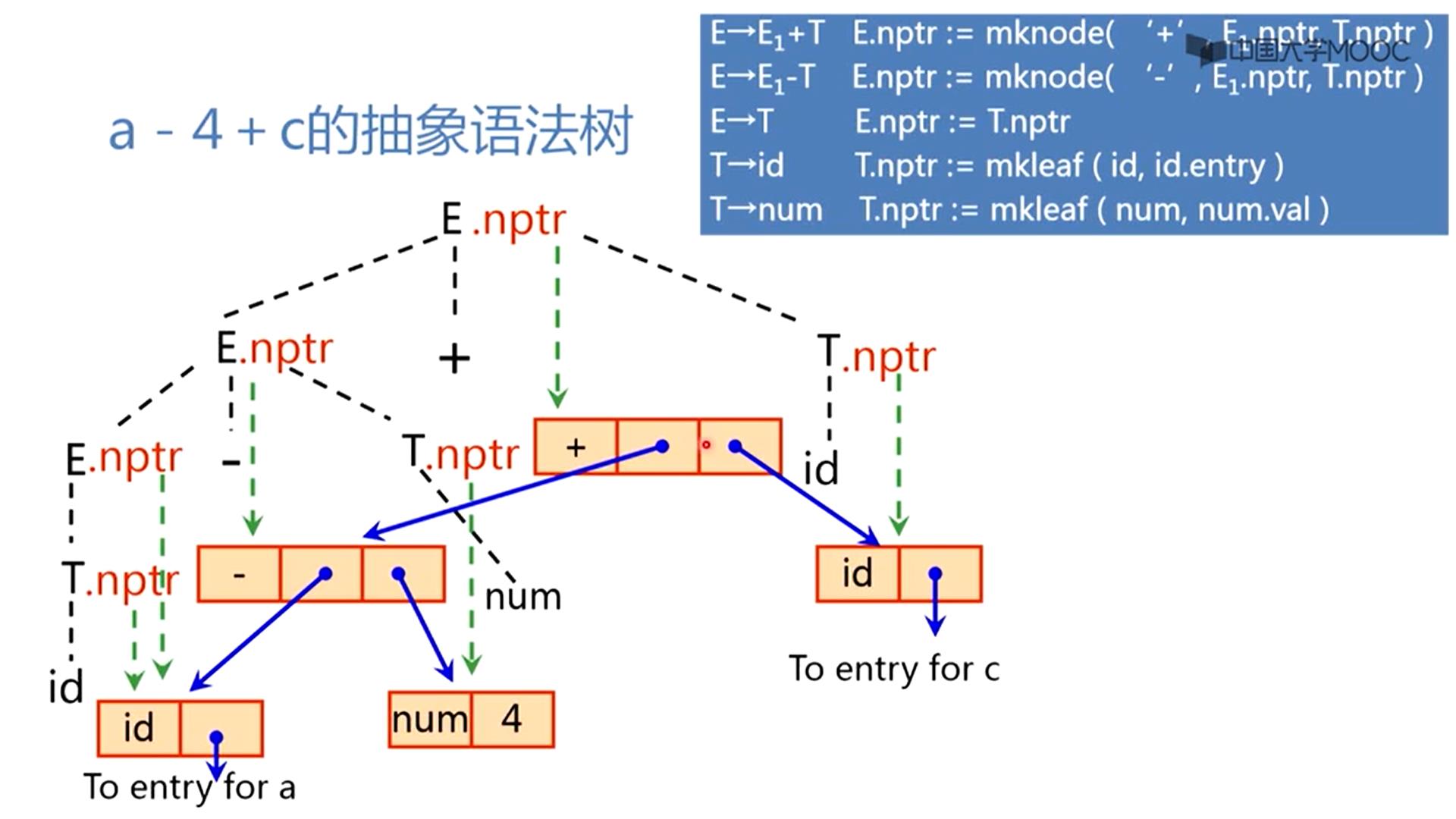
把E+T归约成E,
E→E1+T E.nptr := mknode( ‘+’, E1.nptr, T.nptr )
创建一个+节点
E.nptr指向加法节点,,左边指向左子树E1.nptr指向的这个节点,右边指向右子树T.nptr指向的这个节点。
最后,把整个表达式归约到E上面,E.nptr指向了一个节点,这个节点就是整个表达式所对应的抽象语法树的根
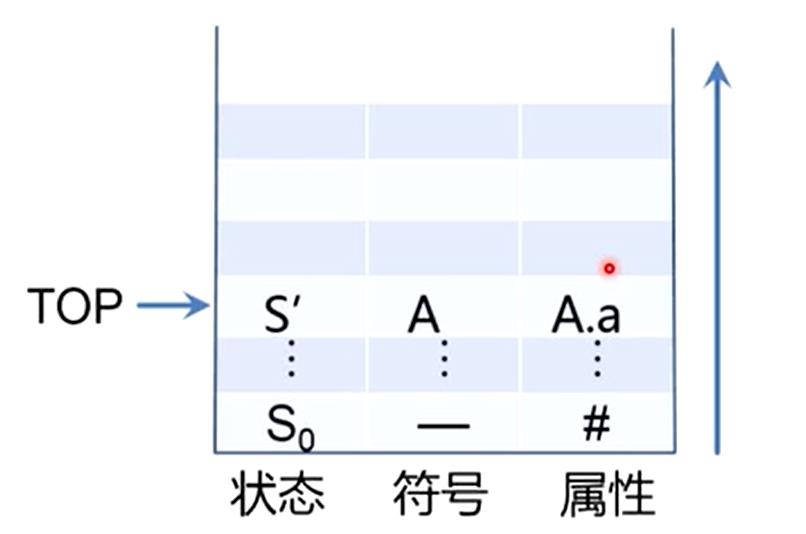
6.3 S-属性文法的自下而上计算

假设每个符号只有一个综合属性
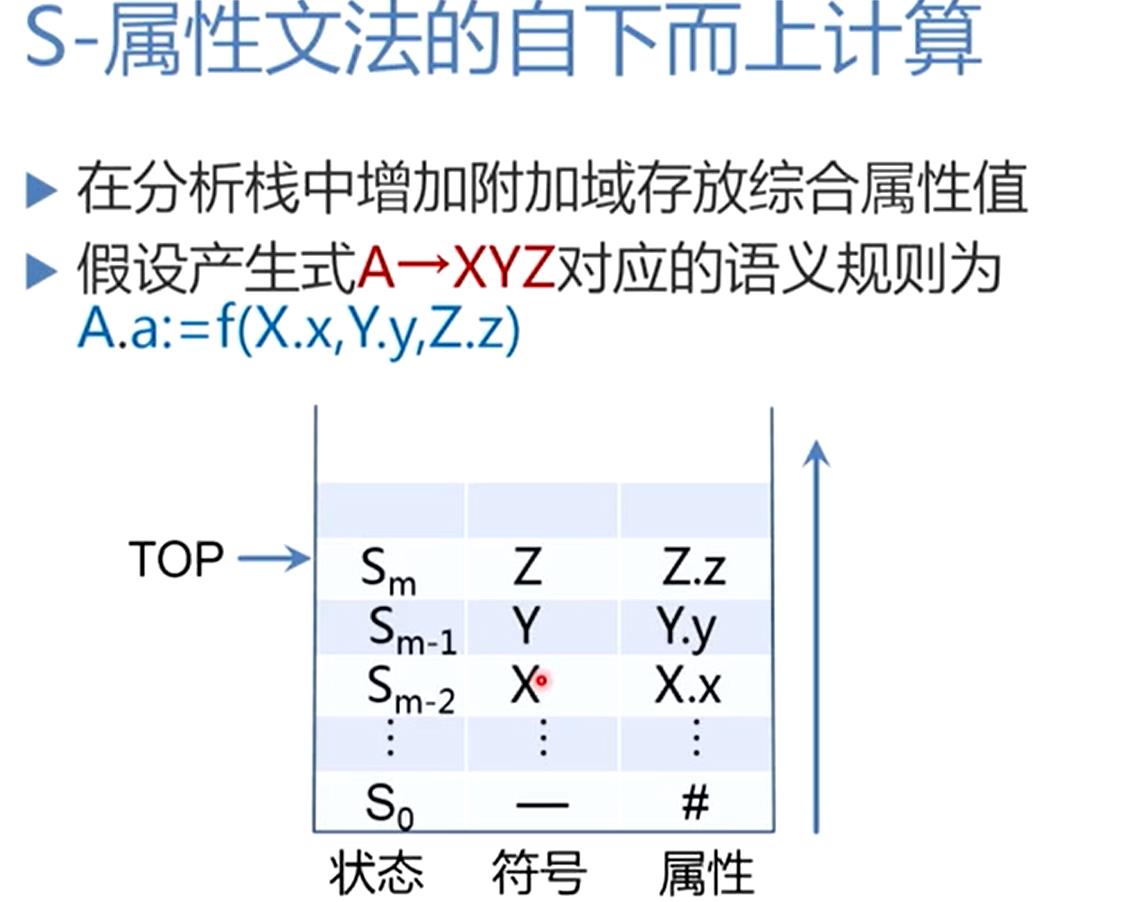
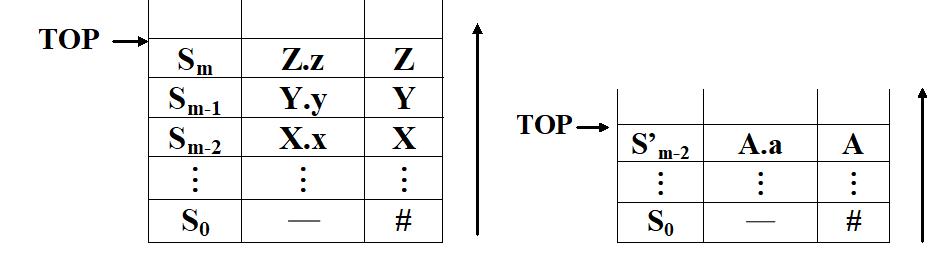
做规约的时候,将栈顶的三个符号弹出来

然后把规约后得到的A,以及计算得到属性值的A.a一并压入栈里面,成为新的栈顶,也就是说,在归约的过程中,完成属性计算。
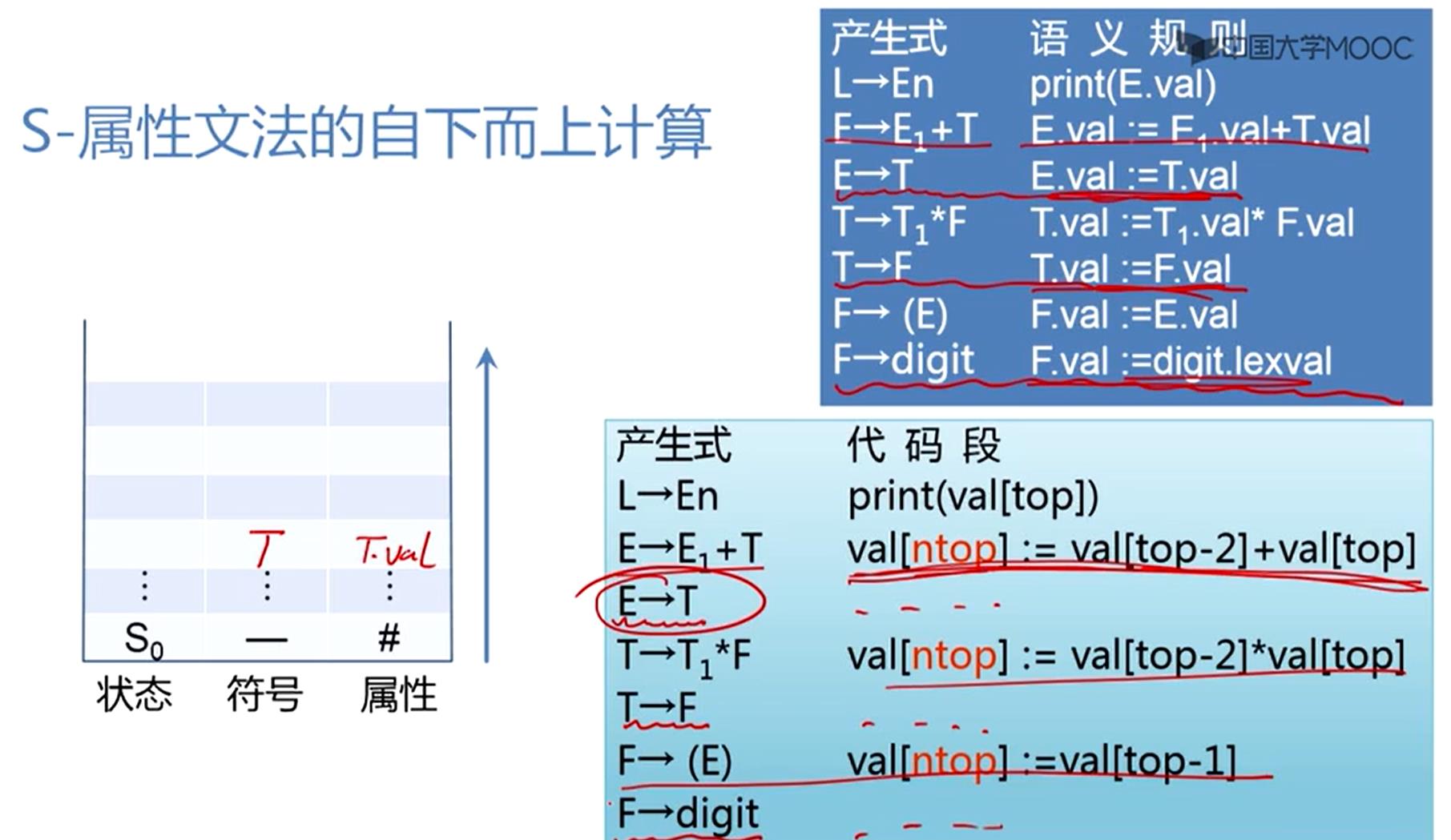
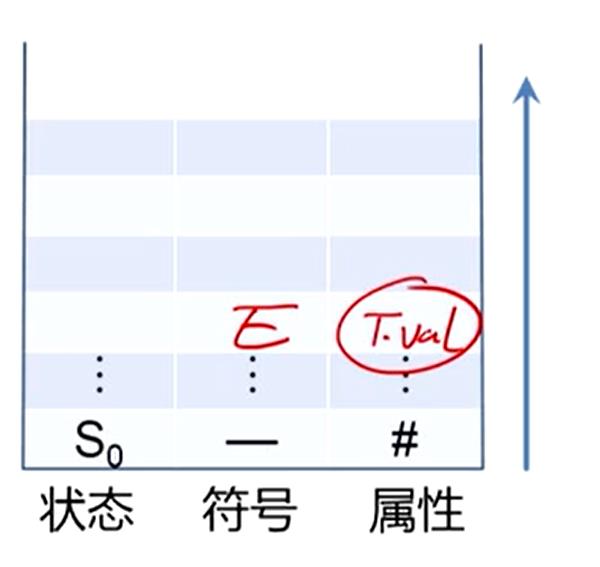
E→T 什么都不做,T拿出来,E进入,属性值的一栏也不会变,相当于将值给了E,实现了把T.val给E.val的语义规则的计算
S-属性文法的分析过程
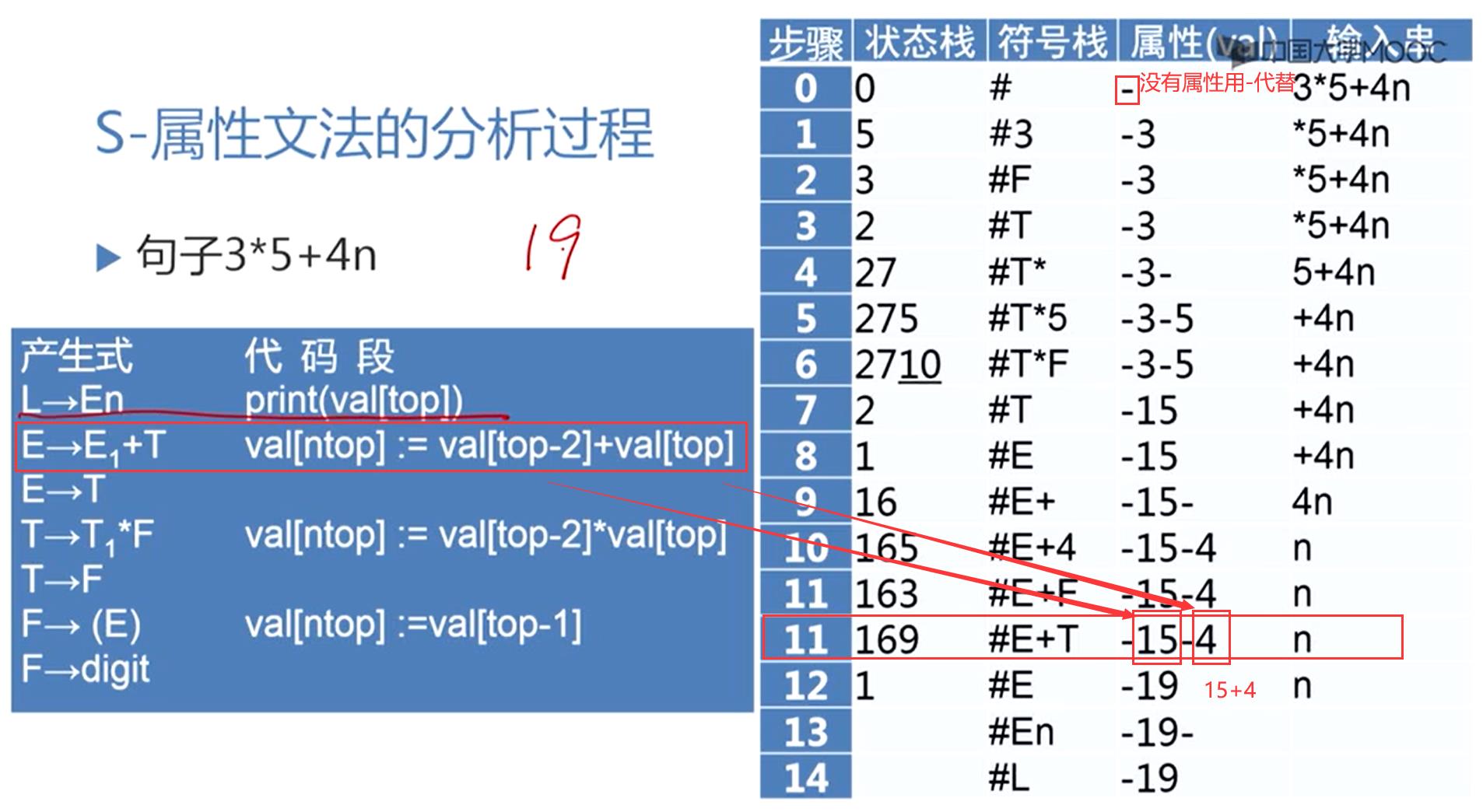
3替换成F,符号栈变化,属性栈没变
F归约为T,符号栈变化,属性栈没变

6.4 L-属性文法和自顶向下翻译


注意:继承属性是指产生式右部符号Xi的继承属性,且产生式右部符号的继承属性不能够依赖于它右边的符号的属性,只能依赖于它左边的符号,以及它父节点的属性来计算
S-属性文法只有综合属性,没有继承属性,所以肯定满足L文法的定义。
测试:L属性文法

原因:第二个产生式有三个语义规则,第二个语义规则说的是,对R.s做q函数的计算,做完了之后,给Q.i,也就是说,在属性计算上面,Q的继承属性的计算是依赖于它右边的符号R的属性来计算的,不满足L属性文法条件。(L属性文法要求产生式右边的符号的计算属性不能依赖于它右边的符号的属性,Q的继承属性只能依赖于它左边的符号,包括A,不能依赖它右边的符号R),所以说这条属性规则破坏了L属性文法的条件。
6.4.1 翻译模式



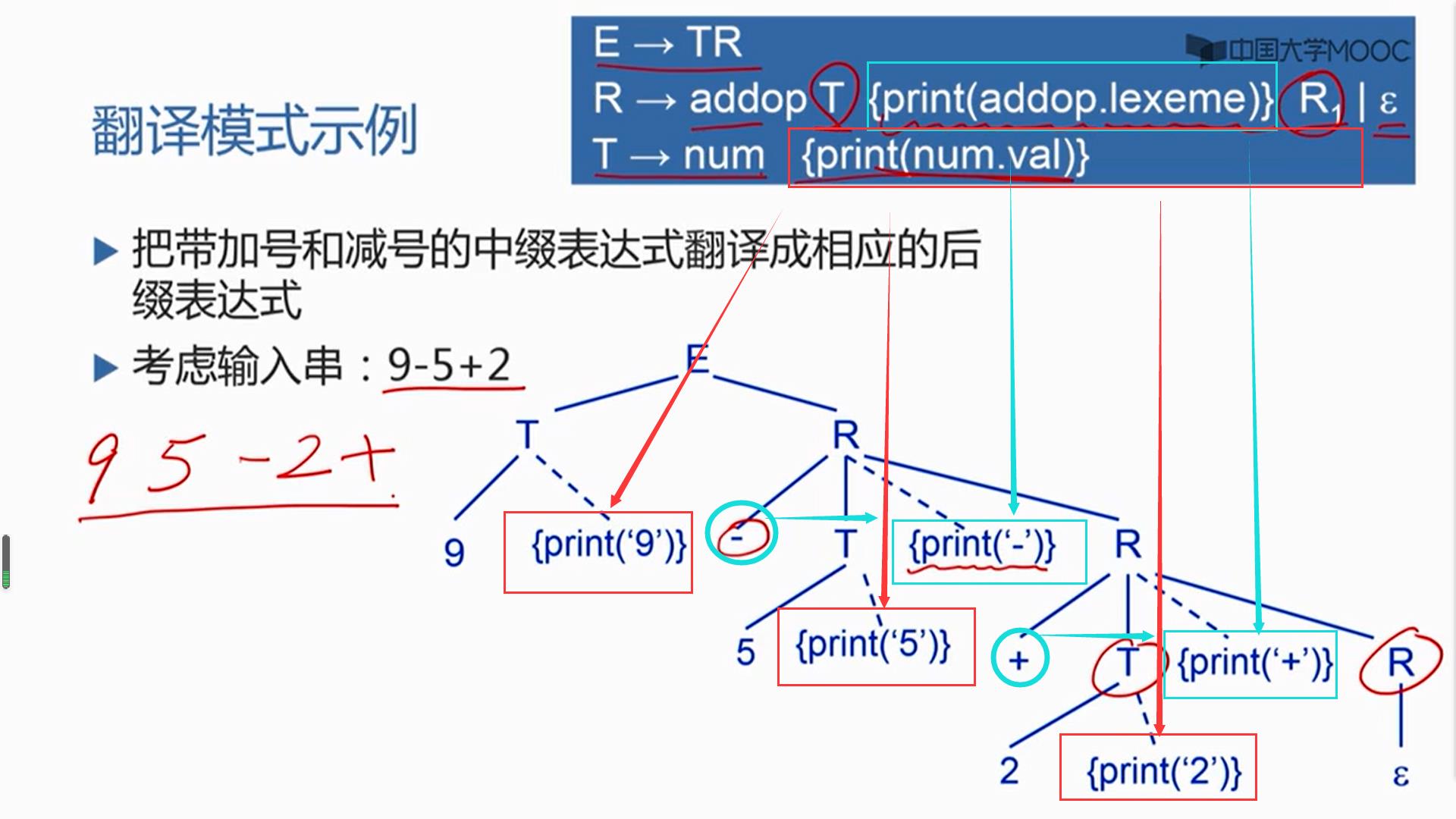
设计翻译模式的原则


对于列子T→T*F,它的语义规则设计产生式和语义动作只需要将语义规则打上花括号放在产生式的最右端,及跟在F的后面,因为父节点综合属性的值只依赖子节点,将综合属性计算的语义规则放到产生式的最右边,它的子节点都已经扩展完毕了,所以这些属性值也都具备了,综合属性可以这样安排,当然,如果所依赖的子节点在前面某个位置上就都已经计算出来了的话,那么综合属性的语义动作还可以往前提,但是不管怎么说,把它放在右边的末端一定是可行的
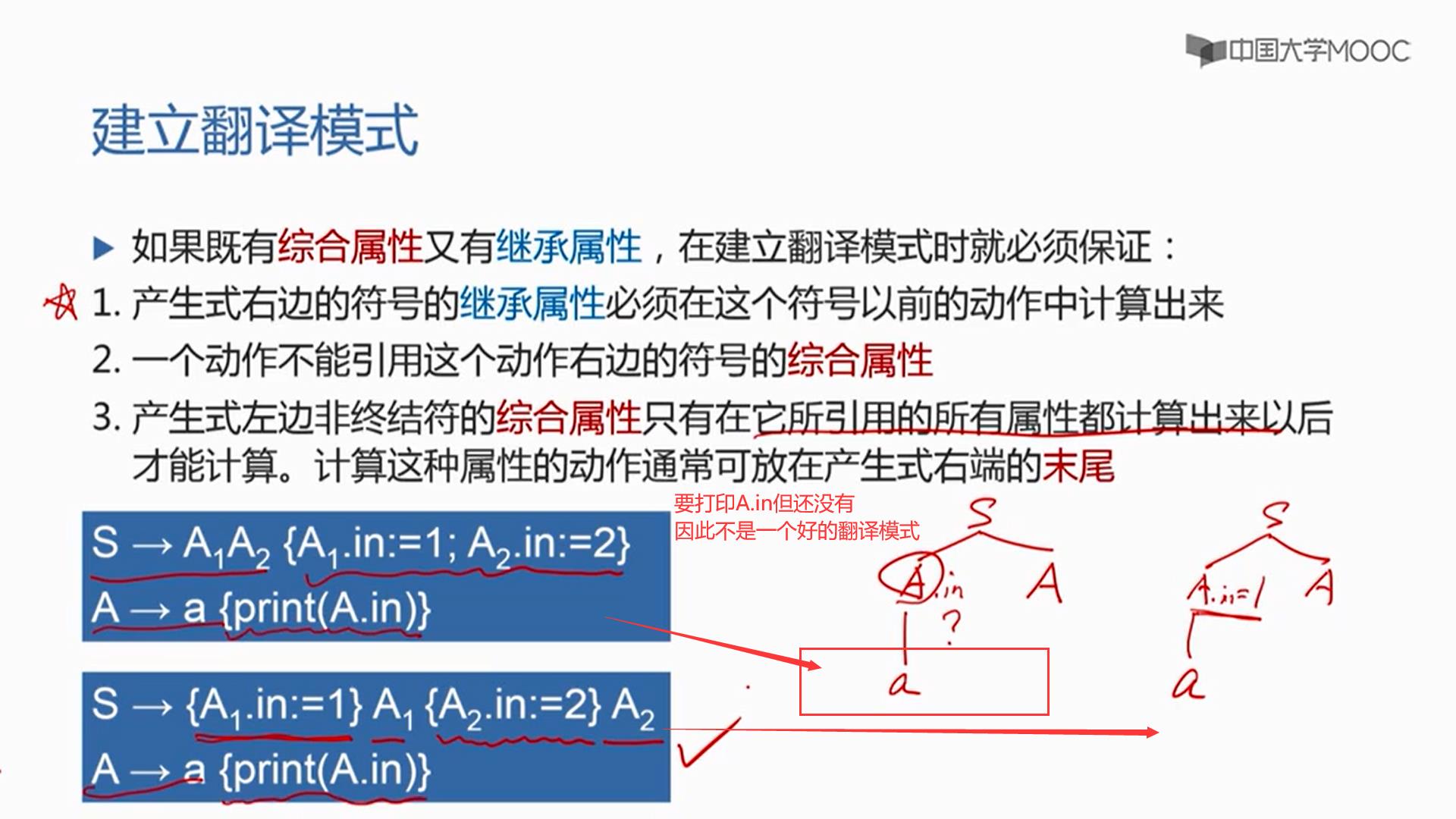
第一个例子不满足第一条:关于A1继承属性A1.in的计算和A2继承属性A2.in的计算都不应该给放在A1,A2的右边,不满足第一条:

也就是说A1.in应该在A1之前计算出来,A2.in应该在A2.in之前计算出来:改进!
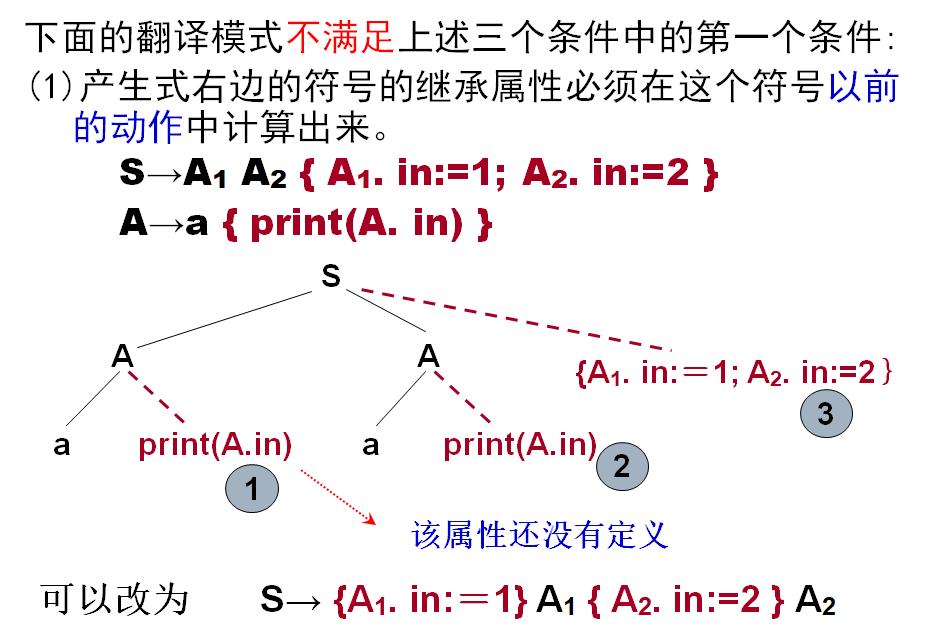
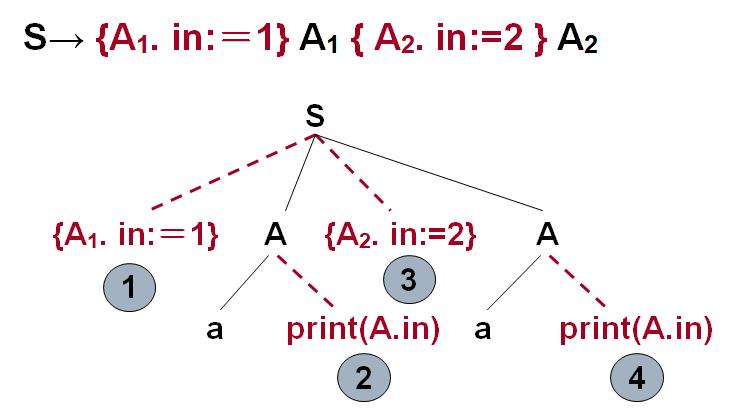

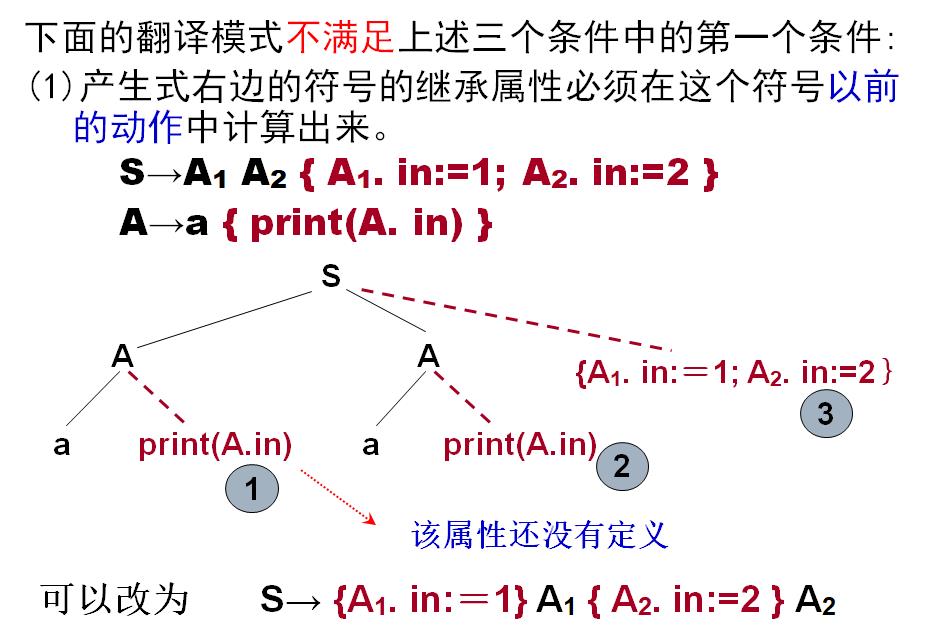
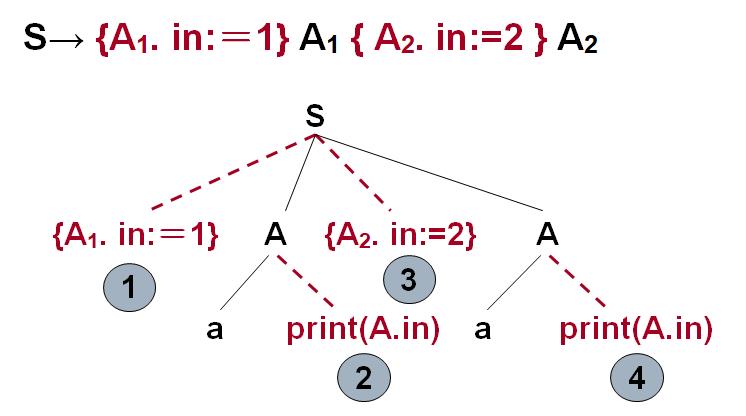
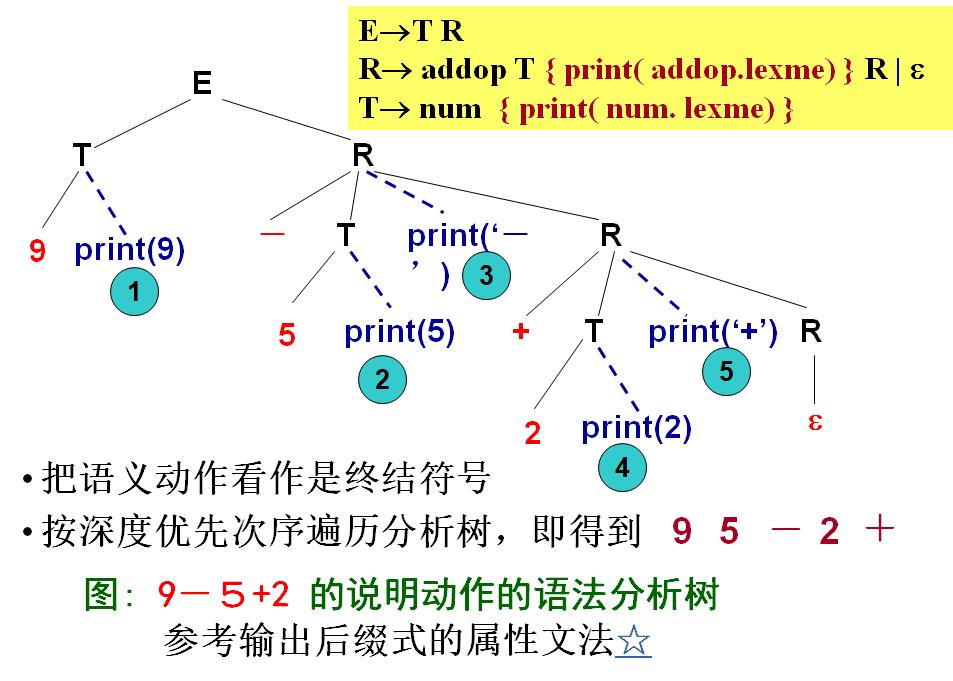
翻译模式示例

基于数学格式语言的EQN
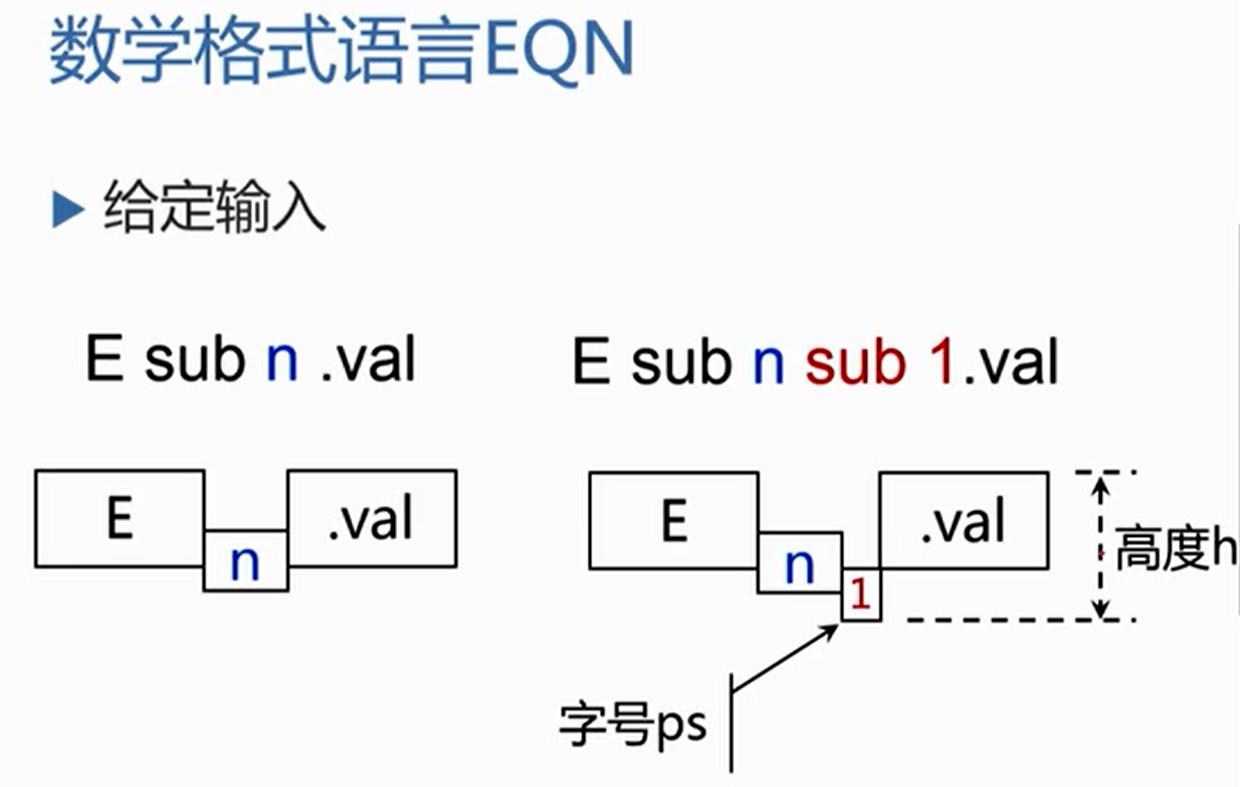

S→B代表整个句子可以由一块文本构成,B代表一块文本,整个句子的正文大小是10,因此必须告诉B整个句子的正文大小是10,B.ps=10,当B处理完了后,所有文本都处理完了,整个句子高度就是整个S这个句子呈现出来的高度,注意ps是B的继承属性,ht是B和S的综合属性
B→B1B2第二条产生式说的是一段文本可以有两端文本并置而成,它的语义说的是前面这一段文本的准确大小就是父节点告诉的准确大小,后面这一段文本的准确大小也是父节点告诉的准确大小,两端文本他们的准确大小一样。
第三条规则说的是,前面一段文本B1,前面一条文本的高度是后面两个文本高度的最大值,就是他们两个拼起来之后整个文本的高度
B → B1 sub B2 说的是一段文本可以由一段文本B1加上后面下标B2构成,sub表示后面是下标,B1还是正文,所以B1的准确大小就是父节点告诉的准确大小,而B2是下标,所以说B2的大小应该是在父节点告诉我们的大小基础上缩小一点,将缩小的比例通过shrink函数来实现,也就是说B2.ps一定会比B1.ps要小,然后第三条规则说的是,整大文本的高度是由前面的B1的高度和B2的高度做一个错位的放置之后,最高点到最低点的距离,就是我的整个文本的高度,把刚才错位放置之后计算这两个文本最高点到最低点的距离都由disp的函数来实现,返回结果给B.ht
B→text 最后,如果B就是一个纯粹的字符文本的话,整个文本的高度就是由文本有多少行text.h可以理解为文本的多少行,然后B.ps是这个文本准确的高度,准确的字号大小,二者相乘就是这一段文本的高度。


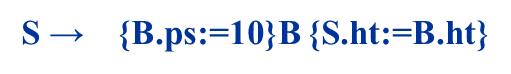
对于第一条规则,它的语义规则B.ps的计算是B的继承属性应该放在B之前,S的综合属性的计算,按照第三条,应该放在B的后面也就是产生式的最右端。
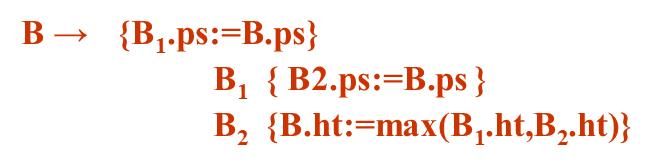
对于第二条规则,按照第一条B1.ps的计算放在B1之前,B2.ps的计算放在B2之前,(这都是B1,B2的继承属性,所以应该放在各自之前)然后关于左边符号B的综合属性,它的计算放在整个产生式的最右端。

考虑第三条语法规则,B1的继承属性ps的计算放在B1之前,B2.ps的计算放在B2之前,左边符号的综合属性放在最右端
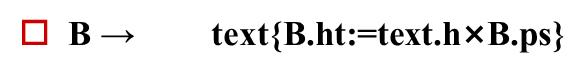
最后一条规则只有一条综合属性的计算,也放在最右端。

这样一来所有的语义动作都统一了
6.4.2 自顶向下翻译



为消除左递归新引入的非终结符R配置它的两个属性
- R.i: R前面子表达式的值
- R.s: 分析完R时子表达式的值(R之前包括R执行完后表达式的值)


①将T的值交给R的继承属性,R往下代,R.s里面有R之前包括R执行完后表达式的值,因此这个表达式的值应该是整个E的值,因此在R执行完了后有E.val:=R.s
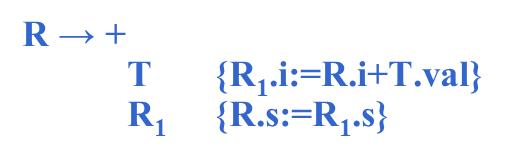
②+和T扩展完了后
把父节点R带过来的i属性(R之前表达式的值,+之前表达式的值)+加号后面紧跟着的表达式的值,将二者做加法。R1.s就是整个R.s综合属性的值。

③-和T扩展完了后
把父节点R带过来 - 号之前的表达式的值和 - 号后面紧跟着的表达式的值做 - 法。减出来的结果就是R1分析之前整个表达式的结果,把它交给R1的i代下去,继续扩展,当R1扩展完了后,R1.s有到目前为止,分析完所有表达式的值,就是R的值
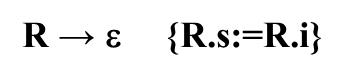
④如果到R → ε,用这个产生式做推导的话,那就到句子结束了,后面没有新的表达式了,R之前分析的结果就是整个表达式的结果,写成语义动作就是把R.i的值传给R.s
最后还有两条规则,它们的动作和原来一样

⑤整个T的值就是E的值
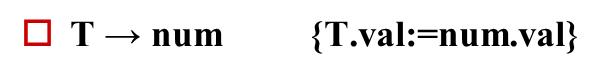
⑥T的值就是num.val
一定要扣住R的两个属性!!!
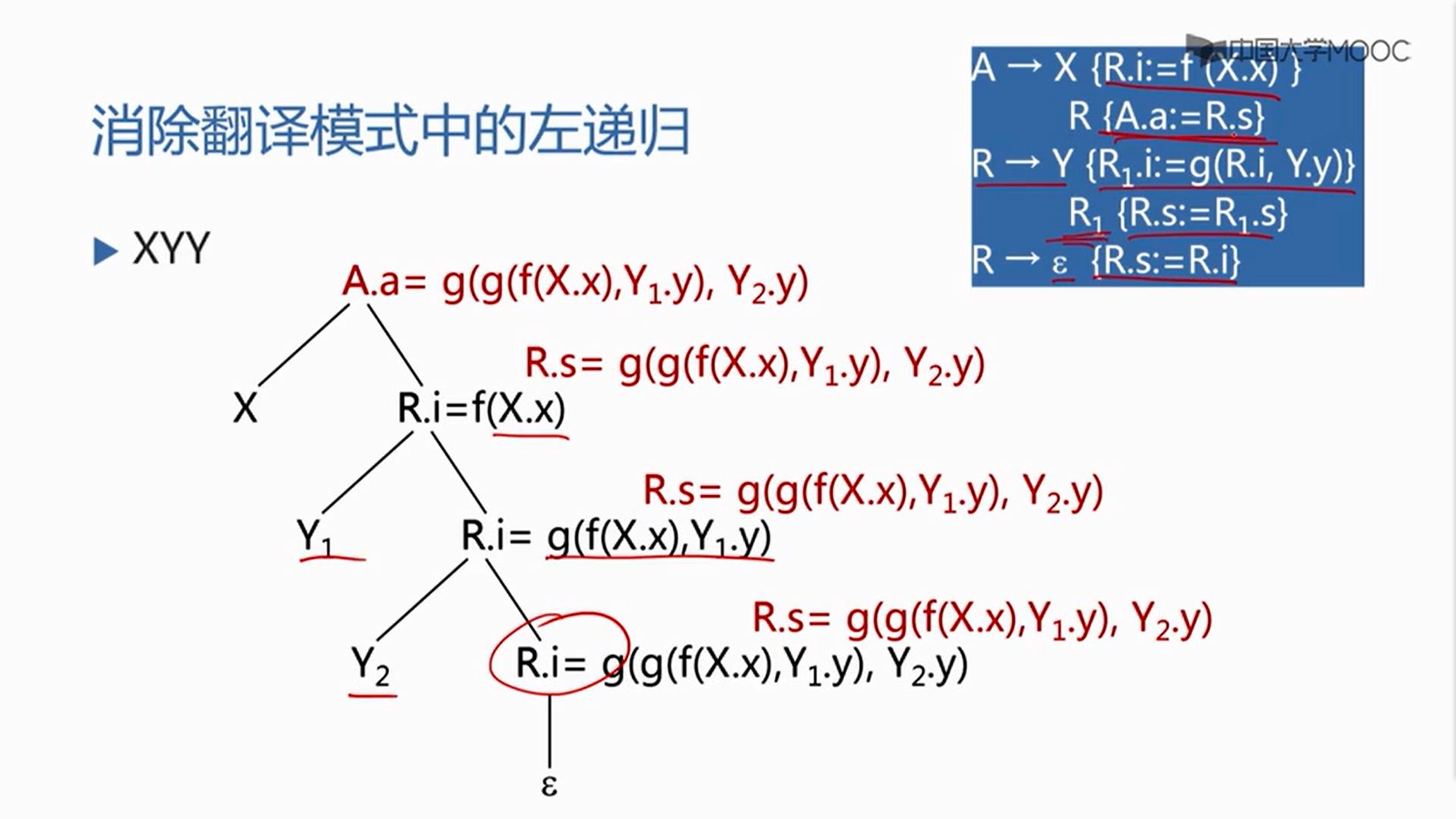
消除翻译模式中的左递归
一边按照表达式自上而下分析,一边按照翻译模式执行相应的语义动作,从而得到表达式的值。
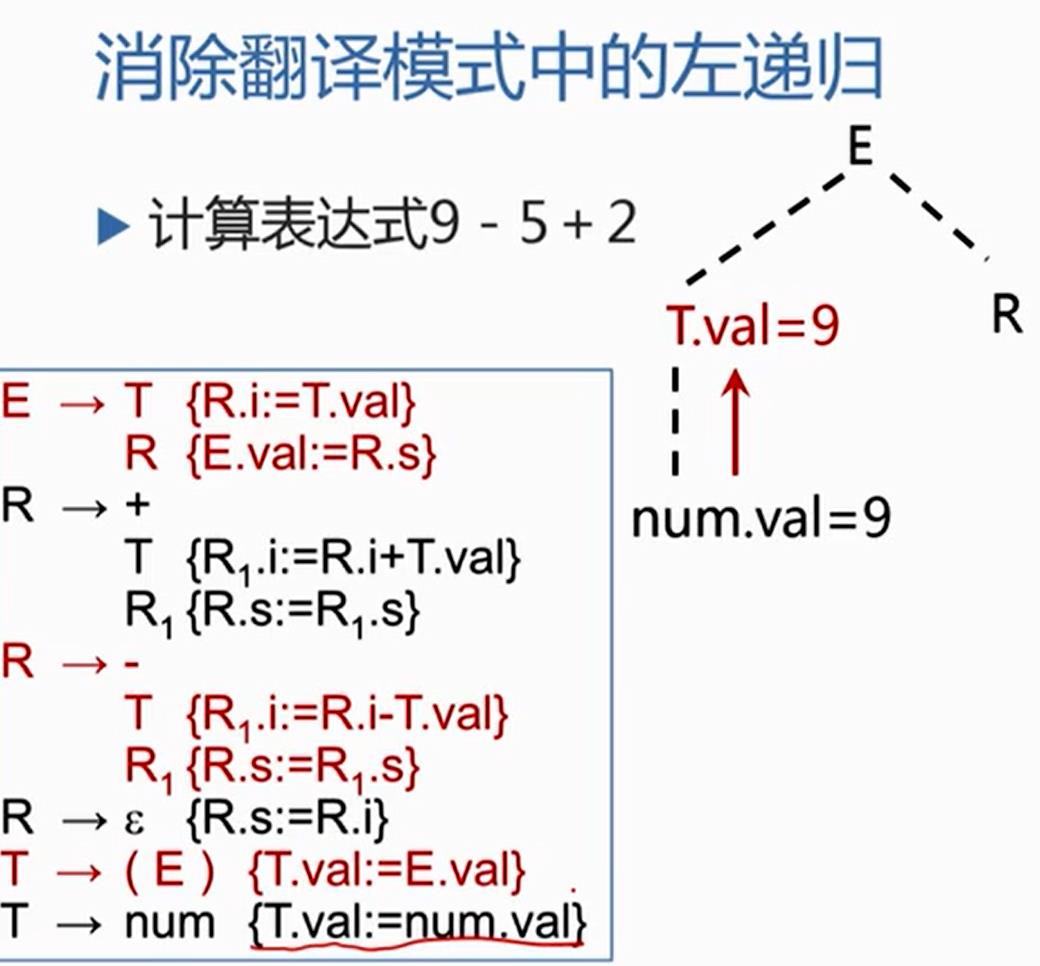
从E开始,扩展为T,R,T跟9匹配,9被识别为种别编码是num,自身的值是9,注意,T扩展为num之后,有一个语义动作,是把T.val置成num.val,所以T.num=9,T处理完了
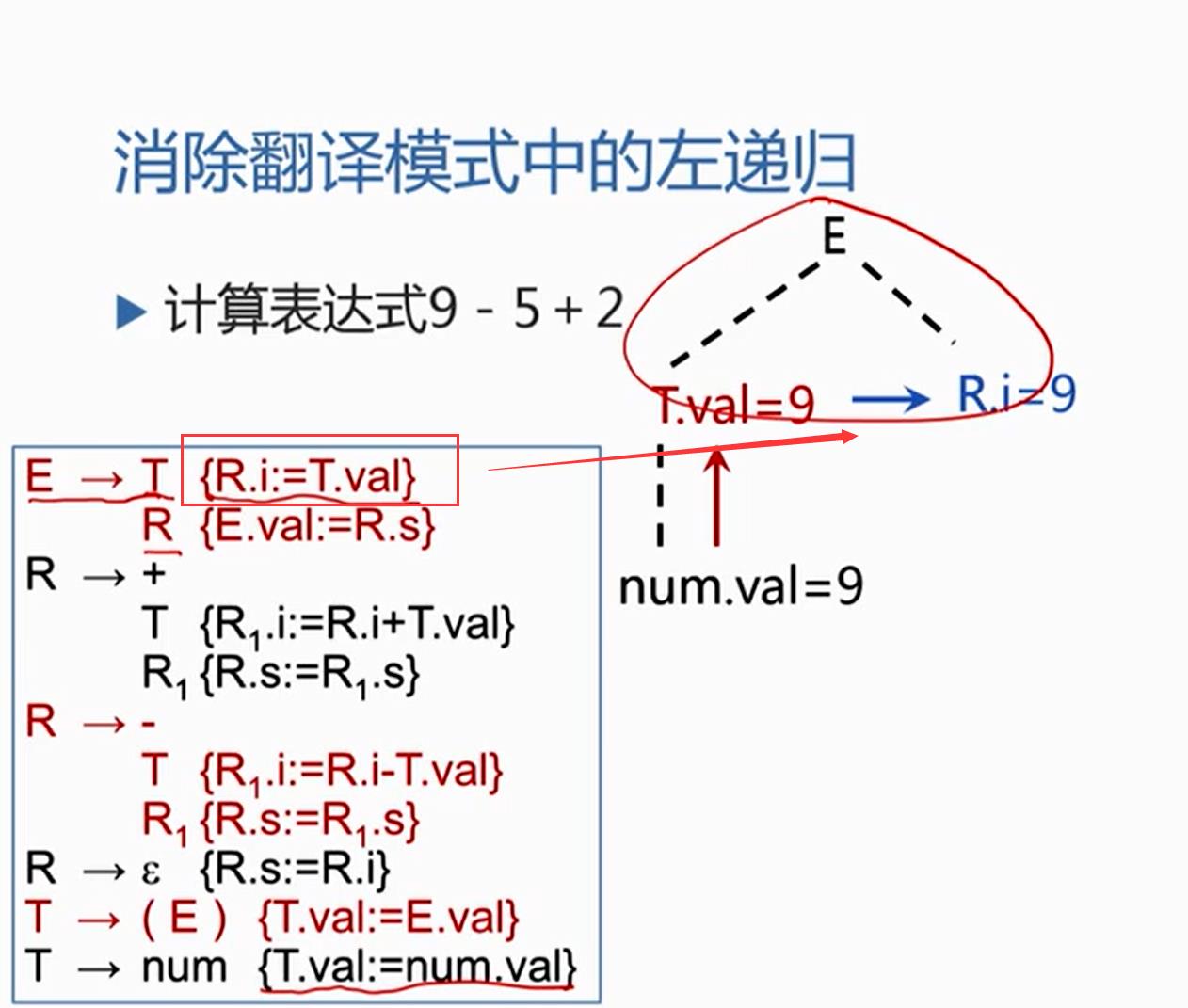
到上面的语法树,在T完了后,{ R.i:=T.val }
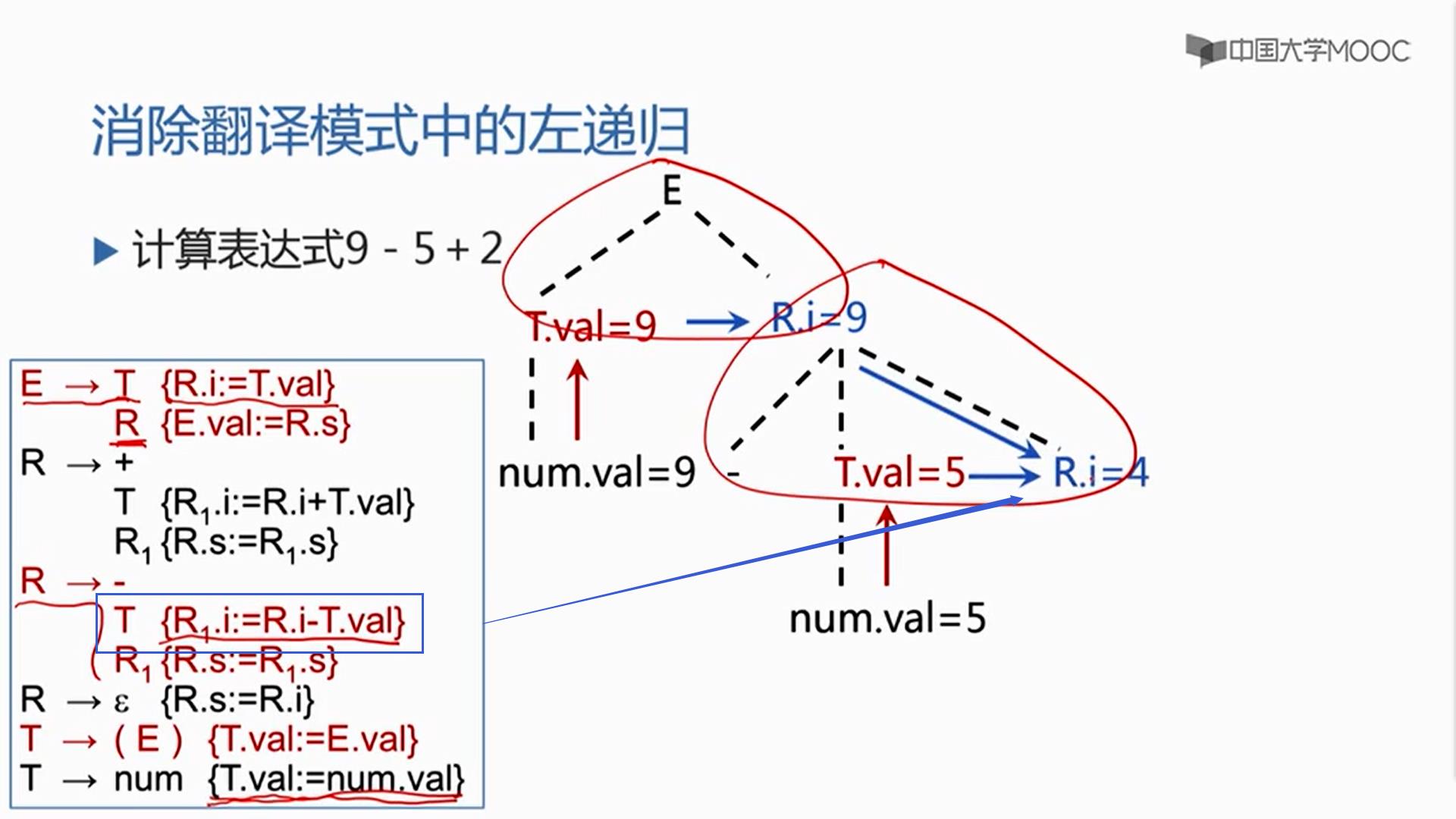
然后再开始R的扩展,R扩展为-,T,R,-和-匹配,T跟5匹配,5被识别为种别编码是num,自身的值是5,注意,T扩展为num之后,有一个语义动作,是把T.val置成num.val,所以T.val=5,T完了后
{ R1.i:=R.i-T.val }
把父节点带过来 - 号之前的结果R.i=9和T的结果-号之后的T.val=5做减法,送到R的继承属性中R1.i=4,然后再开始后面那个R1的扩展。
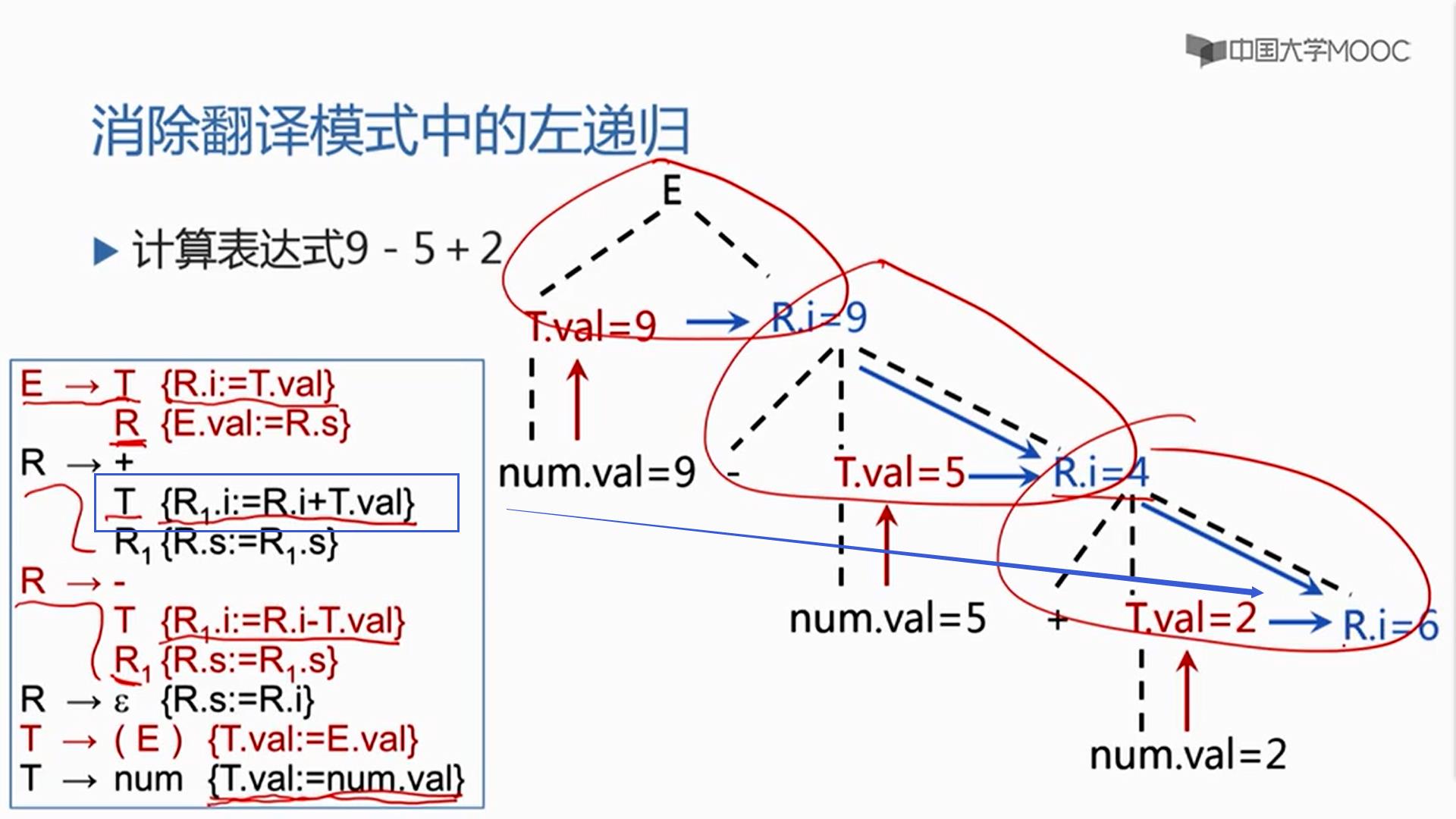
R扩展为+,T,R,+和+匹配,T跟2匹配,2被识别为种别编码是num,自身的值是2,注意,T扩展为num之后,有一个语义动作,是把T.val置成num.val,所以T.val=2,T完了后
{ R1.i:=R.i+T.val }
把父节点带过来 - 号之前的结果R.i=4和T的结果+号之后的T.val=2做加法,送到R的继承属性中R1.i=6,然后再开始后面那个R1的扩展。

这个时候句子结束R跟ε匹配,跟ε匹配完了后后面的结果R的综合属性R.s是他继承属性的值这个时候,R执行完毕,回到了这棵树,注意,+,T,R这个时候结束,执行这个动作
{ R.s:= R1.s }
父节点的综合属性,等于最右边子节点的综合属性,这个时候第二个R结束,执行R-TR1第三个动作,父节点的综合属性,等于最右边子节点的综合属性,第一个R结束,执行ETR第二个动作,拿到E的综合属性
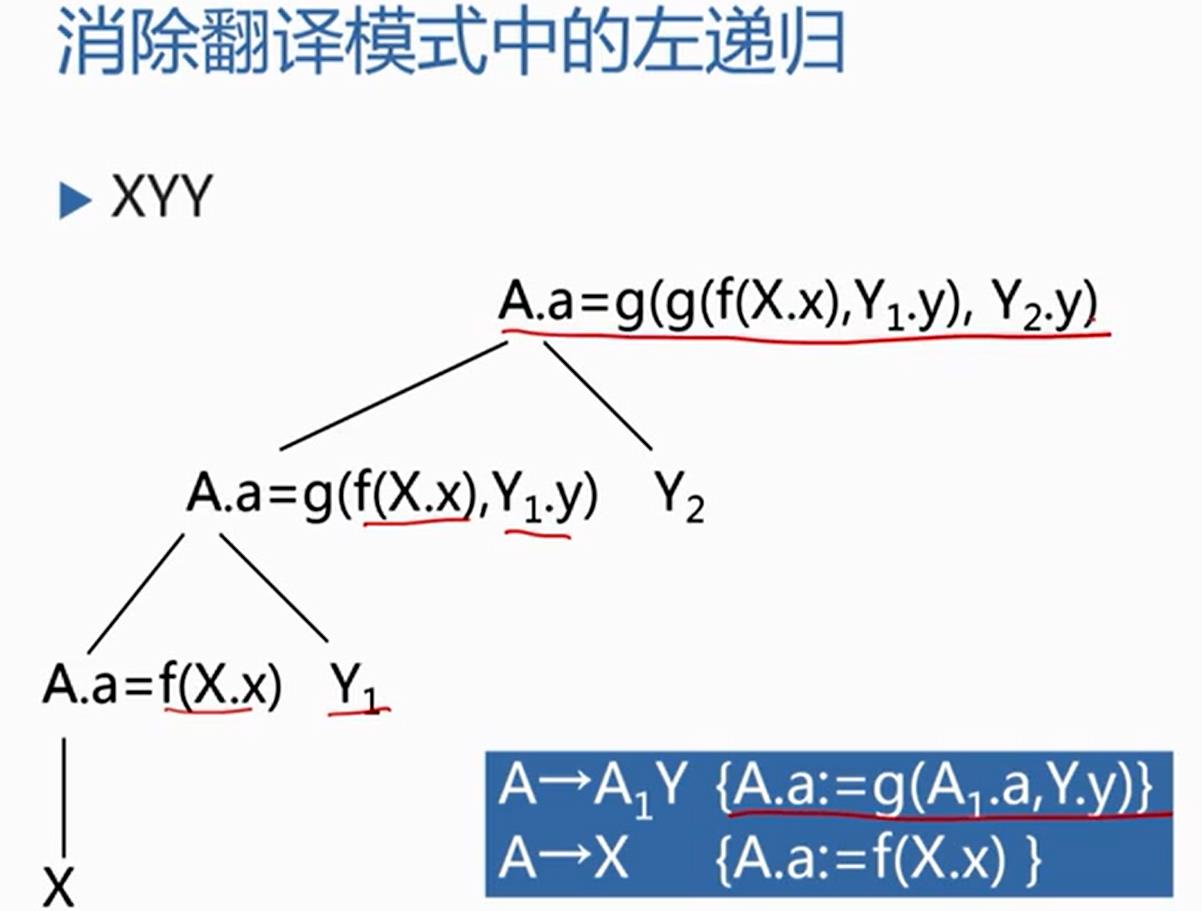
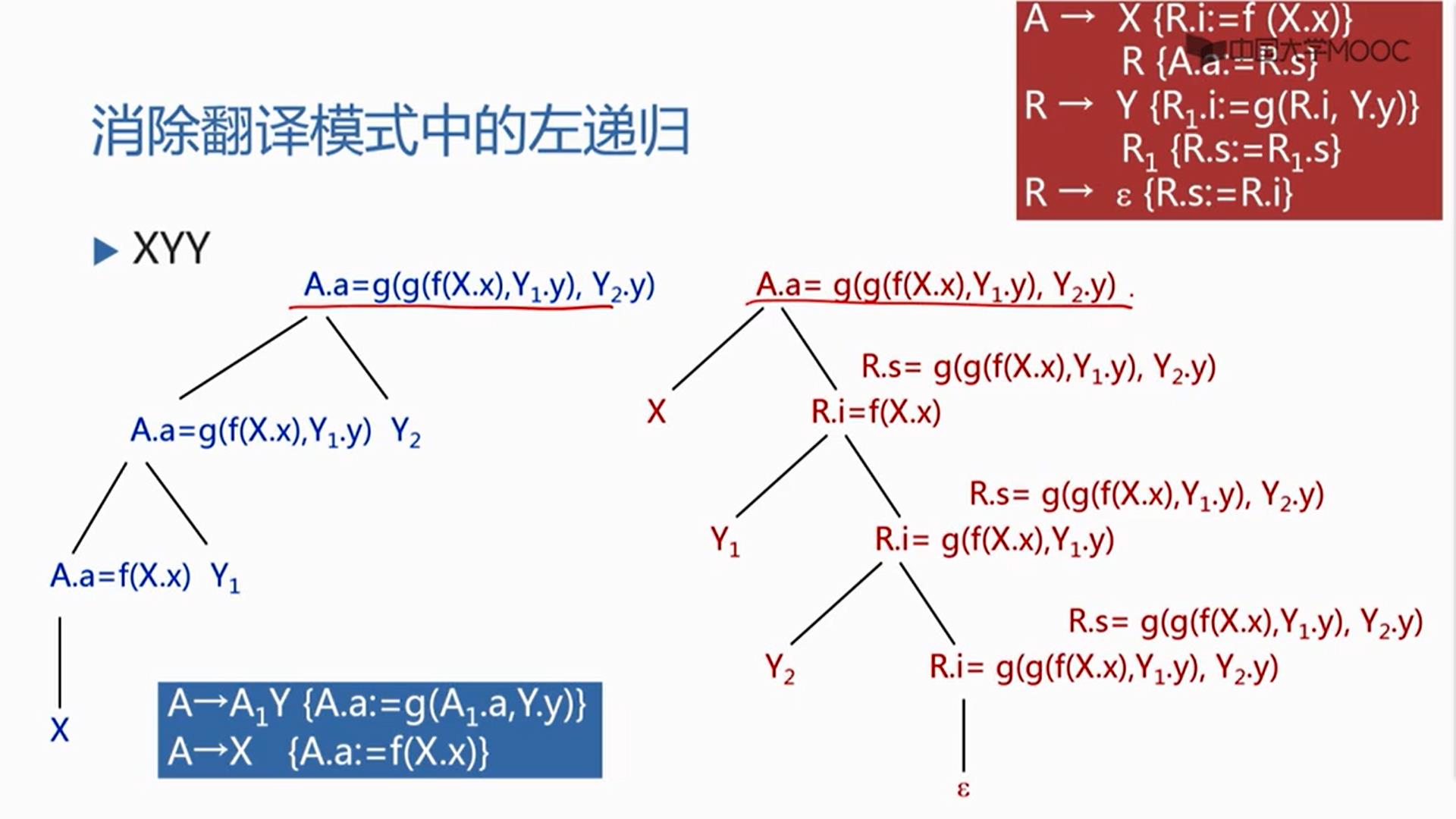
对消除左递归模式进行推广:

在第一个产生式的X和R之间放上语义动作
{R.i:=f (X.x)}
先按照第二个产生式的动作得到以X为参数经过f变换后的结果,也就是说对X处理的结果,放到了R的继承属性i里面,当R处理完了之后,整个A的综合属性就拿R的综合属性就行了。
(R继承属性是R之前的属性计算结果,R综合属性是R匹配完了之后整个属性的计算结果)下面R的第一个候选将会插入两个产生式,在Y和R之间插入产生式
{R1.i:=g(R.i,Y.y) }
把父节点带过来的y之前的处理结果和y自己的结果做g函数运算,也就是实现了原来的第一条规则
A→A1Y {A.a:=g(A1.a,Y.y) }
这个部分的动作,结果送给谁,送给即将要开始的R的继承属性,因此这个R1的继承属性就是他前面已经处理完的属性计算结果,然后再对R1进行展开,R1展开完了后再从R1的继承属性中拿到整个R的综合属性值{R.s:=R.i}
如果R到了句末,后面没有什么东西了,他跟空匹配,那么R带过来的R之前的处理结果,就是R处理完了之后,整个的处理结果。
对原来含有左递归的翻译模式和改造后左递归的翻译模式是不是等价的。含有左递归的翻译模式只能做自下而上的分析:
改造后的消除左递归的计算结果:
不管按照原来的翻译模式进行自下而上的运算还是消除左递归进行自上而下的运算,再语法树的根节点得到的属性计算结果是一样的:
应用于解决具体问题


对于第一条规则

R有一个继承属性是记录R之前已经构造好的翻译完的抽象语法树的根,所以R.i就是T的根,当R处理完了之后,R的综合属性所挂上的抽象语法树是整个表达式的抽象语法树的根。
第而条规则
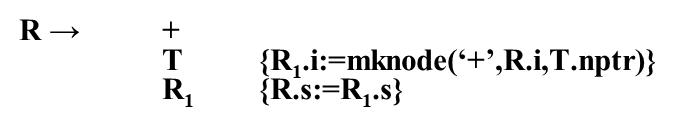
把父节点带过来的抽象语法树的根和加号后的T的抽象语法树,都挂在+号下面,并且返回给R1的继承属性,R1的继承属性就是R1前面翻译完的抽象语法树的根,R1处理完了后R1.s里面就有整个表达式的抽象语法树翻译的结果,交给父节点返回,同样可以理解-TR里面的一些动作
另外注意一下 R → ε {R.s:=R.i}
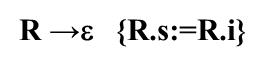
他的动作是R之前翻译好的抽象语法树就是R之后的那部分的抽象语法树,其他T的变化跟原来一样。
对翻译模式进行应用
自上而下分析
(虚线是语法分析的结果语法树
实线是翻译的结果就是a-4+c按照翻译模式翻译出来的抽象语法树)
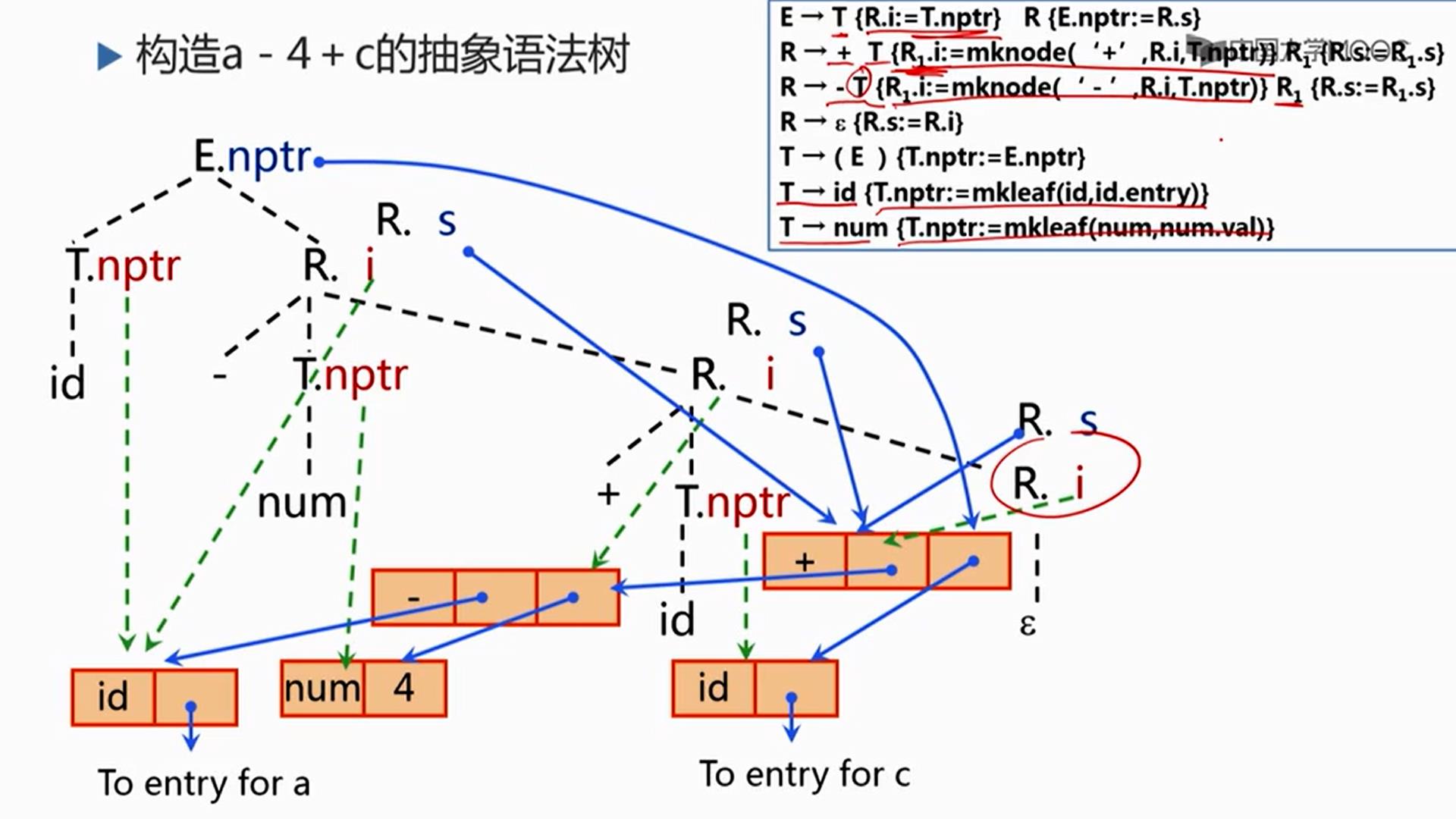
E扩展为T,R,T扩展为标识符id,它的语义动作:
T → id {T.nptr:=mkleaf(id,id.entry)}
创建一个叶节点,由T.nptr指向它,T扩展完了,之后,把T的结果给R的继承属性,R.i也指向这个节点,然后扩展R为-,T,R,-号与-号匹配,T跟4匹配,4是num按规则
T → num {T.nptr:=mkleaf(num,num.val)}执行,创建一个num,由T.nptr指向它,这时候T处理完了该执行R → - T {R1.i:=mknode(‘-’,R.i,T.nptr)} R1 {R.s:=R1.s}
中的 {R1.i:=mknode(‘-’,R.i,T.nptr)} 动作,这个动作说的是创建一个-节点,左边挂上父节点的内容(指向id节点)右边挂上T的内容,整个mknode的节点交给R.i,然后再解决R1也就是这个R的扩展
第2个R扩展为+,T,R,T跟c匹配
T → id {T.nptr:=mkleaf(id,id.entry)},
创建一个叶节点T.nptr指向它,这个时候这个地方要执行的动作我们相当于执行+完了,T完了,得执行R → + T {R1.i:=mknode(‘+’,R.i,T.nptr)} R1 {R.s:=R1.s}
中的 {R1.i:=mknode(‘+’,R.i,T.nptr)} 动作,这个动作说的是创建一个+节点,左边挂上父节点的内容(指向id节点)右边挂上T带过来的子树,整个mknode的节点交给R.i,后面一个R扩展为ε
扩展为ε后R的综合属性可以算了R → ε {R.s:=R.i}
,就是它的i的结果指向同样的节点
这个R处理完了后,交给父节点的综合属性R → + T {R1.i:=mknode(‘+’,R.i,T.nptr)} R1 {R.s:=R1.s}
中的 {R.s:=R1.s}动作,再交给父节点的综合属性
R → - T {R1.i:=mknode(‘-’,R.i,T.nptr)} R1 {R.s:=R1.s}
中的 {R.s:=R1.s}动作
最后交到E的综合属性E → T {R.i:=T.nptr} R {E.nptr:=R.s}中的{E.nptr:=R.s}
6.4.3 递归下降翻译器的设计




调用B的时候要给参数,c是为B的综合属性设置的变量。


由于E只有综合属性没有继承属性,所以E对应的函数没有输
以上是关于三万五千字长文!让你懂透编译原理——第六章 属性文法和语法制导翻译的主要内容,如果未能解决你的问题,请参考以下文章
