手把手教你深度学习—初识神经网络

Posted 2021-05-16 羽峰码字

 

 

大家好，我是羽峰，接下来一段时间会为大家分享一些深度学习的基本知识，及各种应用，包括回归，图像分类，图像分割，语义分割，DCGAN，pix2pix，SRGAN等。都是讲的比较基础所以起名为【手把手教你】系列，希望这一个系列能帮助你初步认识深度学习及其应用，并找到自己比较感兴趣的方向一直走下去。

今天给大家分享的是【手把手教你】第一篇初识神经网络。

还是老话，我是羽峰，希望我所分享的文章能为您及更多的朋友带来帮助。欢迎转发或转载呀！

 

欢迎关注“羽峰码字”

目录

人脑神经网络

初识神经网络

1. M-P模型

2. 单层感知器

3. 多层感知器

---

人脑神经网络

   

人工神经网络的灵感来自其生物学对应物。生物神经网络使大脑能够以复杂的方式处理大量信息。大脑的生物神经网络由大约1000亿个神经元组成，这是大脑的基本处理单元。神经元通过彼此之间巨大的连接（称为突触）来执行其功能。人脑大约有100万亿个突触，每个神经元约有1,000个！

 

 

• 接收区（receptive zone）：

  树突接收到输入信息。

• 触发区（trigger zone）：

  位于轴突和细胞体交接的地方，决定是否产生神经冲动。

• 传导区（conducting zone）：

  由轴突进行神经冲动的传递。

• 输出区（output zone）：

  神经冲动的目的就是要让神经末梢，突触的神经递质或电力释出，才能影响下一个接受的细胞（神经元、肌肉细胞或是腺体细胞），此称为突触传递。

 

     

 

神经元的主要功能是神经元受到刺激后能产生兴奋，并能把兴奋传导到其它的神经元．神经冲动在生物体内的传递途径是：上一个神经元的突触→树突→细胞体→轴突→突触。

那么，什么是人工神经网络呢？有关人工神经网络的定义有很多。这里，芬兰计算机科学家托伊沃·科霍宁（Teuvo Kohonen）给出的定义：人工神经网络是一种由具有自适应性的简单单元构成的广泛并行互联的网络，它的组织结构能够模拟生物神经系统对真实世界所做出的交互反应。 人工神经网络与人脑神经元功能类似，也具有输入层（相当于人脑神经元的接收区），输出层（相当于人脑神经元的输出区），隐藏层（相当于人脑神经元的传导区）。

 

 

• 输入层：

             输入层接收特征向量 x 。

• 输出层：

             输出层产出最终的预测 h 。

• 隐含层：

          隐含层介于输入层与输出层之间，之所以称之为隐含层，是因为当中产生的值并不像输入层使用的样本矩阵 X 或者输出层用到的标签矩阵 y 那样直接可见。

 

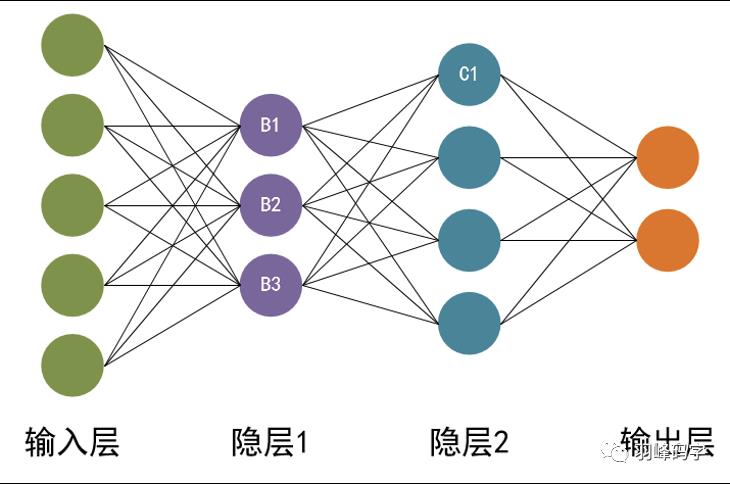
      人工神经网络由一个输入层和一个输出层组成，其中输入层从外部源（数据文件，图像，硬件传感器，麦克风等）接收数据，一个或多个隐藏层处理数据，输出层提供一个或多个数据点基于网络的功能。例如，检测人，汽车和动物的神经网络将具有一个包含三个节点的输出层。对银行在安全和欺诈之间进行交易进行分类的网络将只有一个输出。

---

初识神经网络

1. M-P模型

按照人脑神经元，我们建立M-P模型。为了使得建模更加简单，以便于进行形式化表达，我们忽略时间整合作用、不应期等复杂因素，并把神经元的突触时延和强度当成常数。下图就是一个M-P模型的示意图。

 

将M-P模型和生物神经元的特性列表来比较，来方便理解

                                                                                                            MP模型与人脑神经元比较

M-P模型的6个特点：

1. 每个神经元都是一个多输入单输出的信息处理单元

2. 神经元输入分兴奋性输入和抑制性输入两种类型（取决于权重w的正负）

3. 神经元具有空间整合特性和阈值特性（达到阈值时，神经元才会被激活）

4. 神经元输入与输出间有固定的时滞，主要取决于突触延搁（计算耗时）

5. 忽略时间整合作用和不应期

6. 神经元本身是非时变的，即其突触时延和突触强度均为常数

前面4点和人脑神经元保持一致，这种“阈值加权和”的神经元模型称为 M-P模型 ( McCulloch-Pitts Model )，也称为神经网络的一个处理单元( PE, Processing Element )。M-P模型可以表示逻辑“与”，“或”，“取反”的运算，但这种运算需要人为确定参数，不能通过“学习”得到。

2. 单层感知器

在1958年,美国心理学家Frank Rosenblatt提出一种具有单层计算单元的神经网络,称为感知器(Perceptron)。它其实就是基于M-P模型的结构，单层感知器结构如下图所示。

 

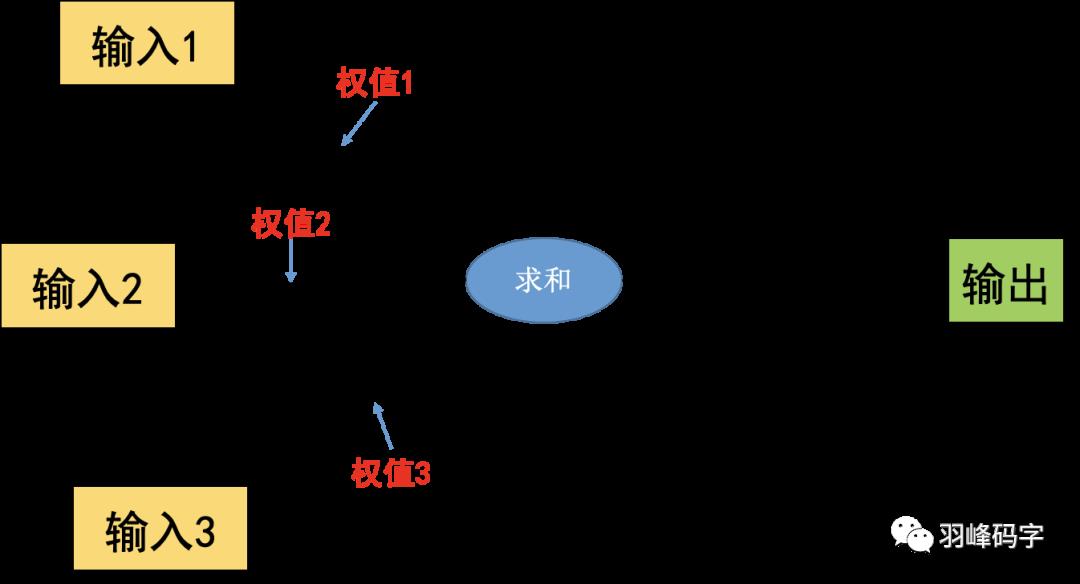
但与M-P模型需要人为设定参数不同，感知器能够通过训练自动确定参数，也就是可以通过“学习”来获取参数。训练方式是有监督学习，即需要设定训练样本和期望输出，然后调整实际输出和期望输出之差的方式（误差修正学习），来调整权值和偏置项等参数。

 

感知器训练过程：

    1. 准备训练

        a. 准备N个训练样本xi，和期望输出ri

         b. 初始化参数w和b

    2. 调整参数

        a. 迭代调整，直到误差为0或小于某个指定数值

            1). 逐个加入样本，计算实际输出

            实际输出与期望相等时，参数不变。

            实际输出与期望不同时，通过误差修正学习调整参数。

            重复步骤“1)”

        重复步骤“a”

 

感知器是最早被设计并实现的人工神经网络，通过误差修正学习，可以自动获取参数，这是感知器引发的一场巨大变革。虽然单层感知器简单而优雅，但它显然不够聪明——它仅对线性问题具有分类能力。什么是线性问题呢？简单来讲，就是用一条直线可分的图形。比如，逻辑“与”和逻辑“或”就是线性问题：

Y=f(w1x1+w2x2-θ)

(1)“与”运算。当取w1＝w2＝1，θ＝1.5时，上式完成逻辑“与”的运算。

(2)“或”运算， 当取wl＝w2＝1，θ＝0.5时，上式完成逻辑“或”的运算。

与许多代数方程一样，上式中不等式具有一定的几何意义。

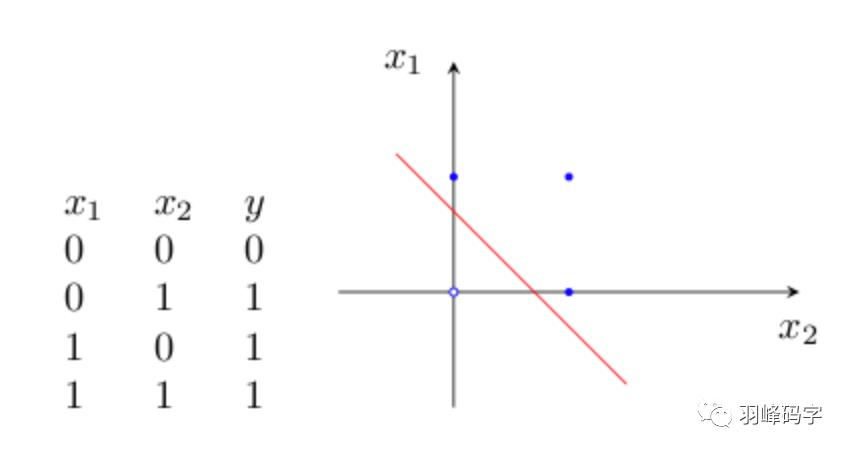
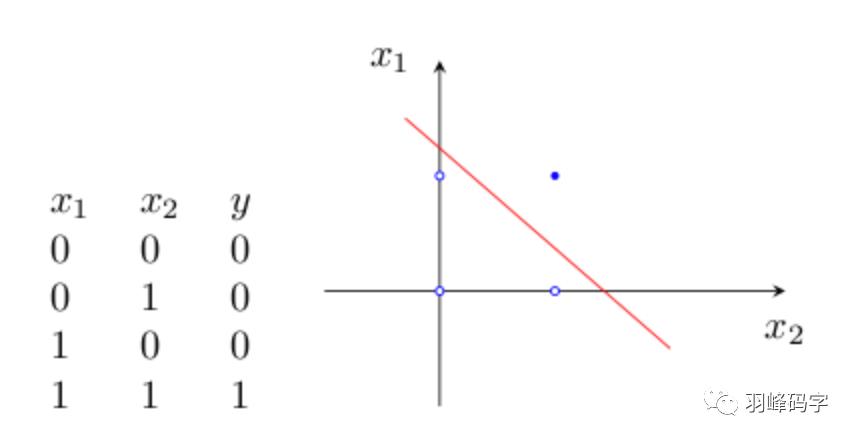
3. 多层感知器

单层感知器的局限在于它只能解决线性可分问题，对于线性不可分问题，它已经不在适用。为了解决线性不可分问题等更复杂的任务，人们提出了多层感知器模型（multilayer perceptron），如图所示

 

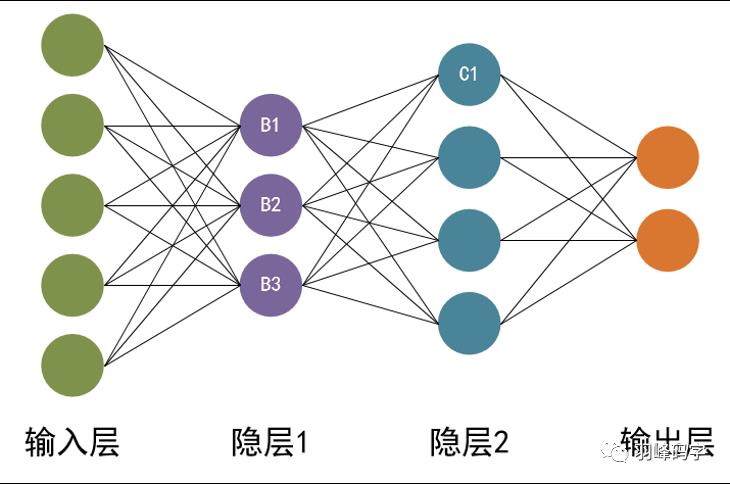
多层感知器模型由输入层，隐藏层，输出层组成，隐藏层的感知器通过权重与输入层的各个单元连接，通过阈值函数计算隐藏层各个单元的输出值。隐藏层与输出层之间同样也是通过权重相连接。多层感知器也是通过误差修正学习来确定两层之间的连接权重，但不能跨层调整，所以无法进行多层训练。因此初期的多层感知器使用随机数去定输入层与隐藏层之间的连接权重，只对中间层与输出层之间的连接权重进行误差修正学习。这样会有很大误差，有时会出现输入数据不同，但隐藏层输出值相同，导致无法准确分类。

为了训练多层网络，人们提出了误差反向传播算法，误差反向传播算法是通过比较实际输出与期望输出得到的误差信号，吧误差信号从输出层逐层的向前传播得到各层的误差信号，在通过调整各层的连接权重以减少误差。权重调整主要使用梯度下降算法。但随着隐藏层数的增加，训练时出现了“梯度爆炸”问题，由于当时技术，这个问题始终没有得到解决，深度学习的研究进入了低潮。

2006年Hinton等人在science期刊上发表了论 文“Reducing the dimensionality of data with neural networks”，揭开了新的训练深层神经网络算法的序幕。利用无监督的RBM网络来进行预训练，进行图像的降维，取得比PCA更好的结果，通常这被认为是深度学习兴起的开篇。

2011年，Glorot等人提出ReLU激活函数，有效地抑制了深层网络的梯度消失问题，现在最好的激活函数都是来自于ReLU家族，简单而有效。

2012年Hinton的学生Alex Krizhevsky提出AlexNet网络，碾压第二名（SVM方法）的分类性能。也正是由于该比赛，CNN吸引到了众多研究者的注意。

从此之后，各种神经网络的提出，使得机器学习及深度学习技术越来越火。

今天开篇就写到这里了，后续会专门讲深度学习的各种应用，敬请期待哦。

我是羽峰，公众号，b站：“羽峰码字”，欢迎来撩。