机器学习理论知识-线性回归

Posted 2021-05-14 cuihaoren01

本专栏用来回顾下，此前学习的各种机器学习理论知识，网上各种资料很丰富，我这边主要借鉴至:
斯坦福大学2014（吴恩达）机器学习教程中文笔记

按照该博主的笔记，结合一些博客，按照我自己想要了解的知识体系进行了归纳。不得不说，up主写的实在是太完美了，把吴恩达老师的笔记整理的透透的。大大节省了观看视频的时间，佩服佩服！

首先就学习下机器学习中最简单的问题—线性回归问题。主要的知识框架如下：

解决哪些问题

线性回归解决的事线性拟合问题，通俗点来说：就是有一系列的自变量$x_i$和其对应的因变量$y_i$，且因变量与自变量满足线性关系，即$y_i=w_i\ast x_i+b$，如果是只有一个自变量一个因变量，就是一元线性回归，如果包含两个或者两个以上的自变量，则称为多元线性回归。

举个例子：（见上述的笔记）

房屋的价格，与房屋的体积存在一定的线性关系。根据调研得到的结果，可以得到如上的表格，我们将其在坐标轴中表示出来。

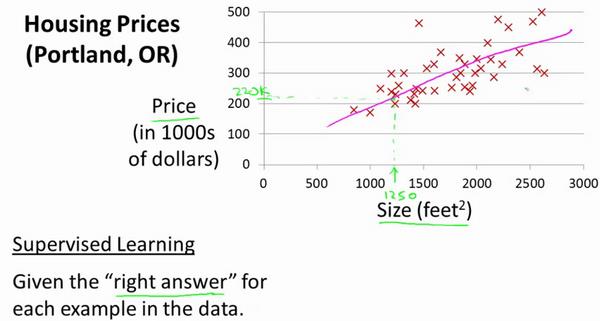
我们的任务就是要得到你看到的那条浅红色曲线的方程式。

多元回归则是存在多个自变量（特征），例子如下：

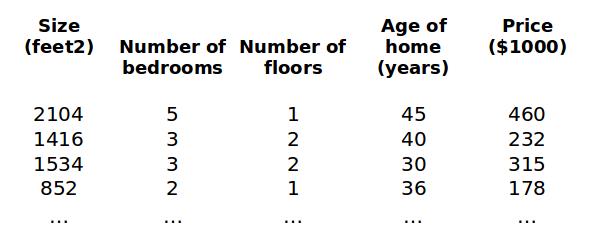
函数表达式

一元线性回归：$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$

多元线性回归：$h_{\theta }(x)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$

如何求解

要拟合自变量与因变量的曲线，那就得使拟合结果($h_{\theta }(x^i)$与真值$y^i$尽可能接近，即使其差值尽可能小，
那就使所有点$（x^i,y^i)$，总的拟合误差达到最小即可。
因此可以考虑以下几种方式：

• 1）用“残差和最小”确定直线位置是一个途径。但可能会出现计算“残差和”存在相互抵消的问题。（从坐标轴看，即一个点在曲线上方，一个在曲线下方，那么其“残差和”可能会被抵消）
• 2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
• 3）“残差平方和最小”确定直线位置。

那么我们要求解的方程为：$J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2$

这里介绍两种方法-梯度下降算法与正规方程（最小二乘法）求解其拟合曲线，并对其进行区分。

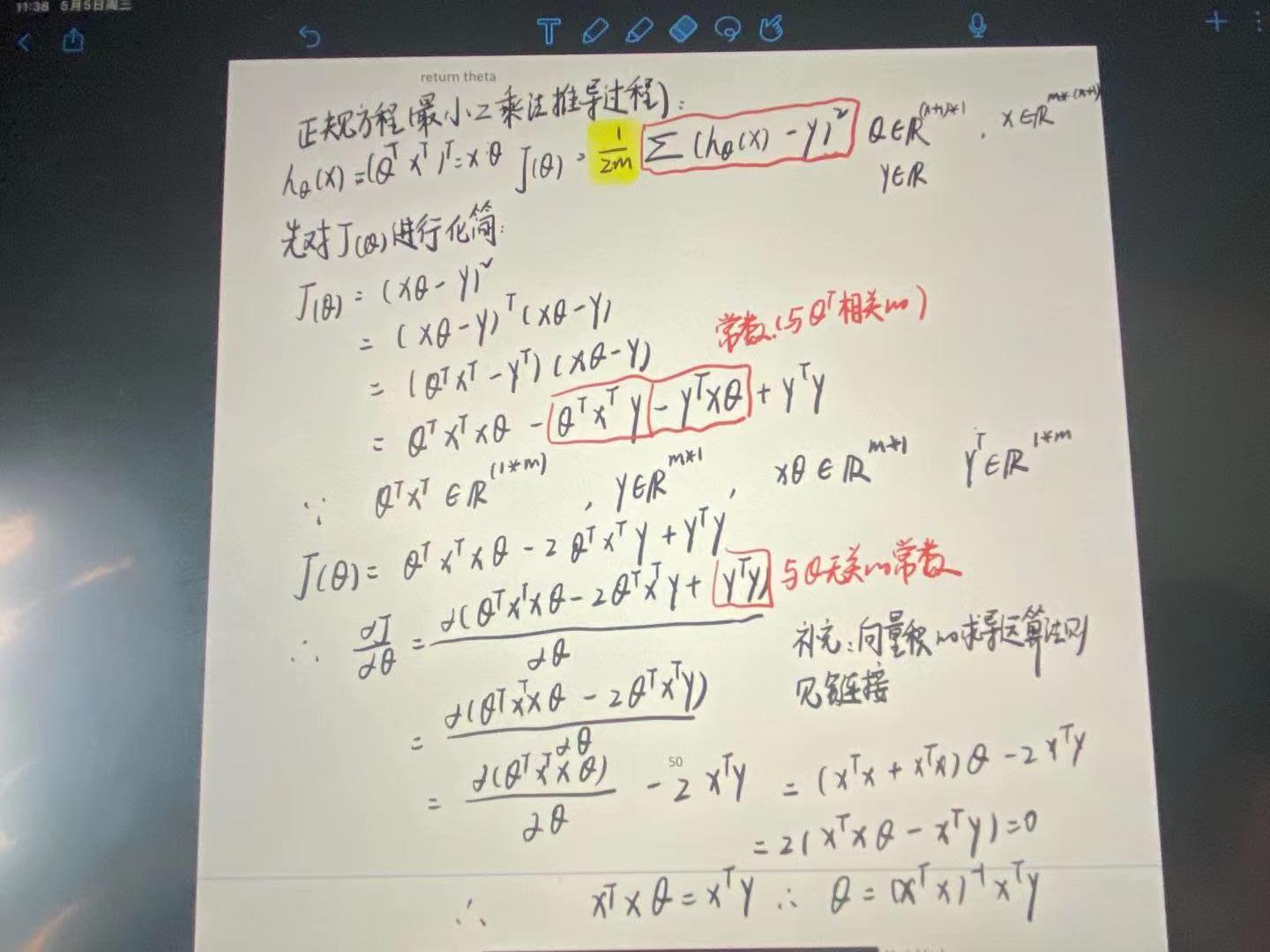
最小二乘法

主要参考的博客：机器学习十大经典算法之最小二乘法

最小二乘法，是通过求解下面的方程来找出是的代价函数最小的参数的$\frac{\partial }{\partial {\theta }_j}J\left({\theta }_j\right)=0$

其推导过程如下：

梯度下降算法

梯度下降算法在求解上与最小二乘法就有不小差别。
通过下图来说明，可以比较形象的理解梯度下降的目的，详细的可以观看吴恩达老师2 - 1 - Model Representation 与 2 - 6 - Gradient Descent Intuition这两个视频

通过不断改变$\theta$的值，来逐步逼近代价函数$J({\theta }_1)$的局部最小值（不是全局哟）。那如何改变$\theta$的值，保证$J({\theta }_1)$的函数值是逐步减小呢。

其推导过程如下：

主要参考的博客：
梯度下降算法原理及推导
为什么局部下降最快的方向就是梯度的负方向？

这里基于笔记在记录一些梯度下降算法的性质：
1、如果参数已经处于局部最低点，那么梯度下降更新其实什么也没做，它不会改变参数的值，因为局部最优点的导数等于0.
2、在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，因为其导数逐渐趋于0。

这里对梯度下降算法不做更深的探讨，后续会专门整理一篇文章关于深度学习梯度下降算法的优化方法，到时候在仔细讨论。

梯度下降法与最小二乘法的区别

梯度下降法与最小二乘法的代价函数基本一致的，仅仅少了一些系数而已，其都是通过最小化均方误差来获取拟合曲线的，其最终目的都是慢慢地找到梯度为0的位置，只不过梯度下降法时通过慢慢地迭代，一步一步地寻找，最小二乘法利用线性函数的性质，一步到位地寻找。

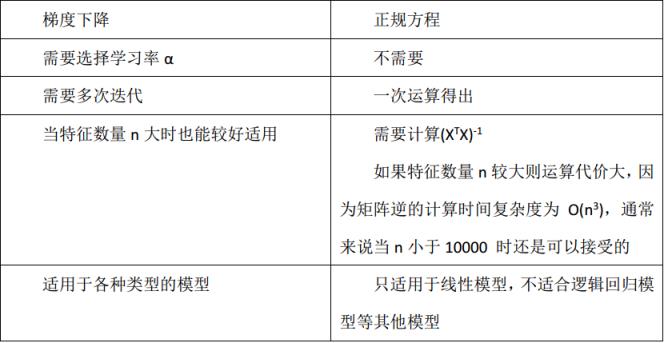
哪些场景适合最小二乘法，而哪些场景使用梯度下降算法呢？
1、当特征变量的数目并不大，最小二乘法时很好计算参数$\theta$的方法。但如果样本的数量小于特征变量的维度时，由于逆矩阵无法计算，所以最小二乘法并不适用。
2、当所有特征中，存在特征之间的线性相关，那么逆矩阵无法计算，同样最小二乘法不适用。
3、梯度下降法的适用场景十分广，只要满足凸函数，都能通过梯度下降法得到全局最优解，（非凸函数，能够得到局部最优解）