AcWing 846. 树的重心 超详细解析

Posted 2021-05-14 幽殇默

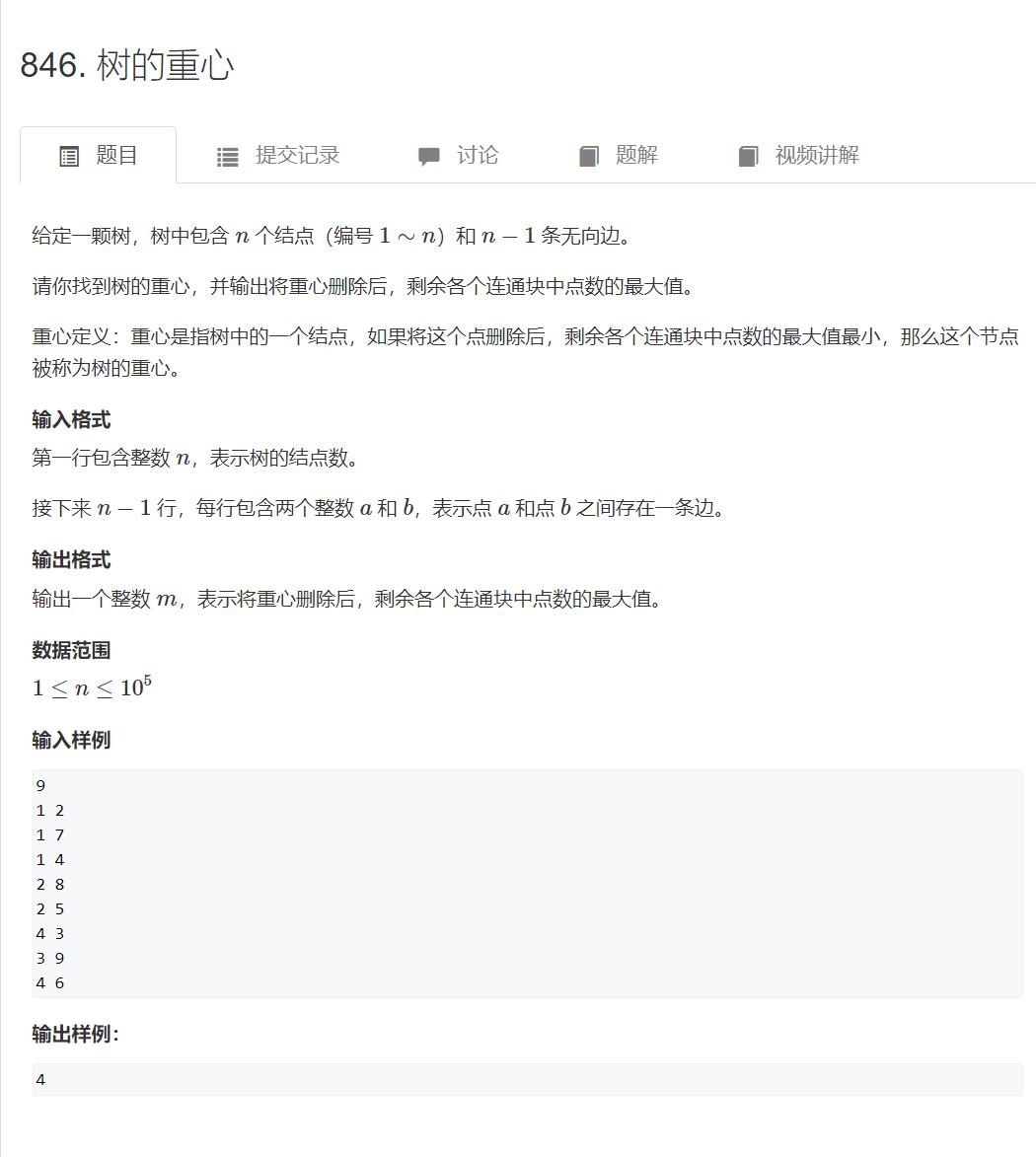
https://www.acwing.com/problem/content/848/

首先要看清题目是 n个点 (n-1) 条边。

重心的定义是啥不多说，不懂的多看几次y总的视频，这不难理解。

题目给的是无向图，我们可以用有向图建两条边，来表示无向图。
题目给的点的范围是 小于1e5。

const int N=1e5+10;
const int M=N*2;
int h[N],e[M],ne[M],idx;
bool st[N];
int ans=N;

所以上面不难理解，因为是两条边故 e[ M ] , ne[ M ] ，头节点就是n个 h [ N ]

st[N]  是用来方式重复遍历的。 因为我们只需枚举每一个点一次就行了。
所以用其标记来保证每一个点只枚举一次

下面开始分析： 如何求去掉一个点后各个连通块点的个数。

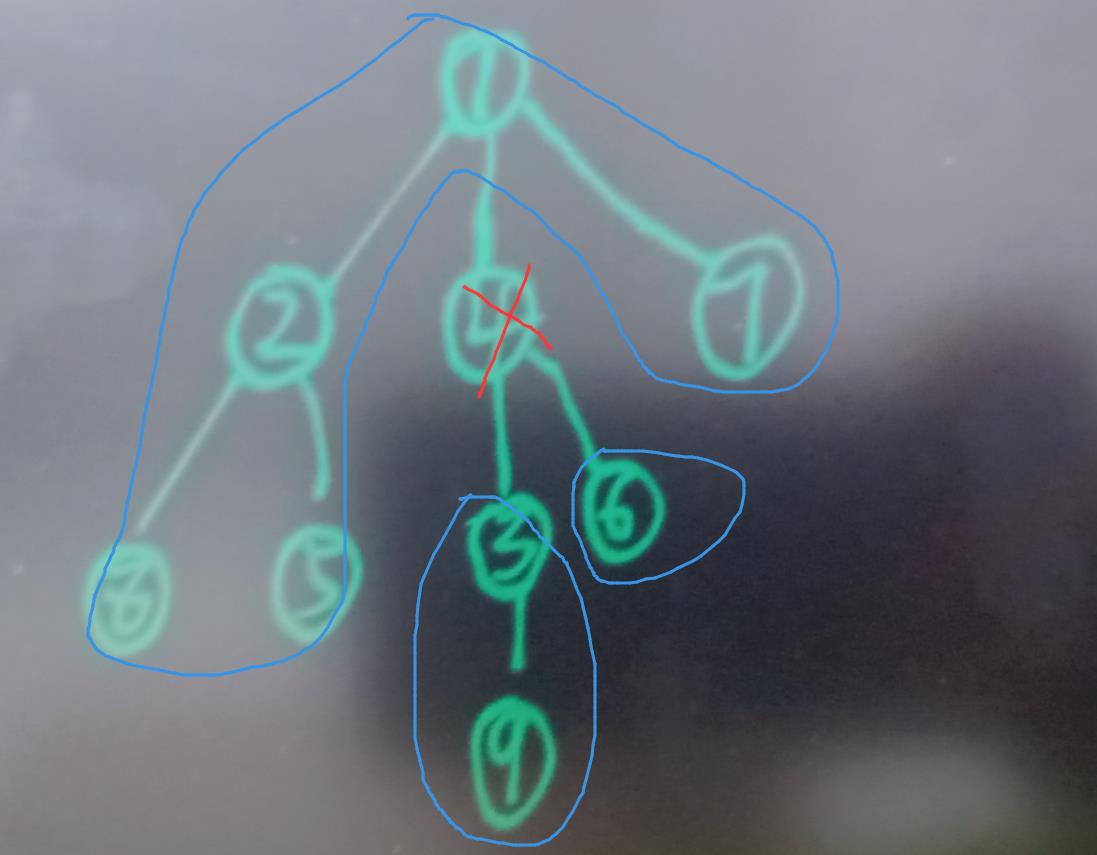
你会发现: 取掉一个点后，此时有三个连通块(用蓝色标记)。

其实本质是两块内容

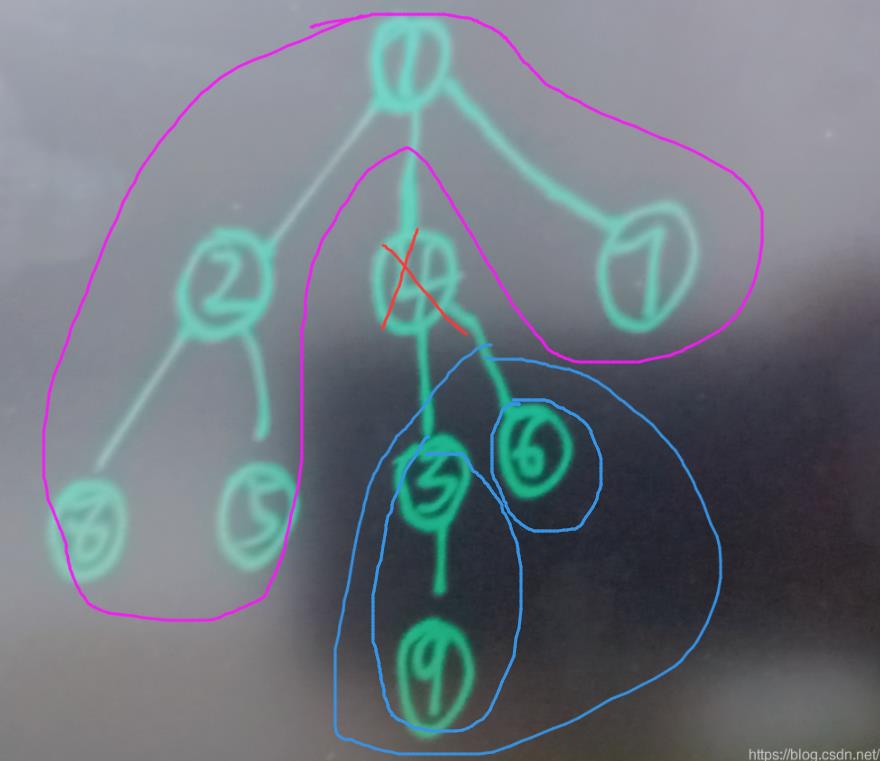
由上图可以看到: 本质分成了两个部分。

• 第一部分： 以4为头节点的其每一个儿子的点的个数(我们取最大的)
• 第二部分： 4作为一个子节点求其所对应的连通块的点数.

那么4作为子节点的点数= n(总的点数) - 4的儿子的节点数之和。

到这里我想各位应该已经懂了一大半了。
下面看代码分析：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10;
const int M=N*2;
int n;
int h[N],e[M],ne[M],idx;
bool st[N];
int ans=N;
void add(int a,int b)//向以a头节点 加入b
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dfs(int u)//求以 u为头节点的子节点的点数之和
{
	st[u]=true;
	int sum=1,res=0;  //sum=1  是因为加上去掉的那个数
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int j=e[i];
		if(!st[j])
		{
			int s=dfs(j);
			res=max(res,s);//  求子节点中点数最大的
			sum+=s; //求以j为头节点的子节点的点数之和
		} 
	}
	
	res=max(res,n-sum);//求头节点所在连通块  和 其子节点最大的点数 中最大的值
	ans=min(ans,res);//求我们每一种情况中，最小的值
	
	return sum;
}
int main(void)
{
	cin>>n;
	memset(h,-1,sizeof h);
	for(int i=0;i<n-1;i++)
	{
		int a,b; cin>>a>>b;
		add(a,b),add(b,a);
	} 
	dfs(4);
	cout<<ans<<endl;
	return 0;
}

首先 因为我这里举的例子是从4开始的，故写的dfs(4) 代表从 4开始枚举。
其实 dfs() 从1到n中的任何一个数枚举都是一样的，因为我们都是只枚举一遍。
不能从0开始是因为我们的节点是从1开始的。你不能枚举一个没有的点。

刚开始：

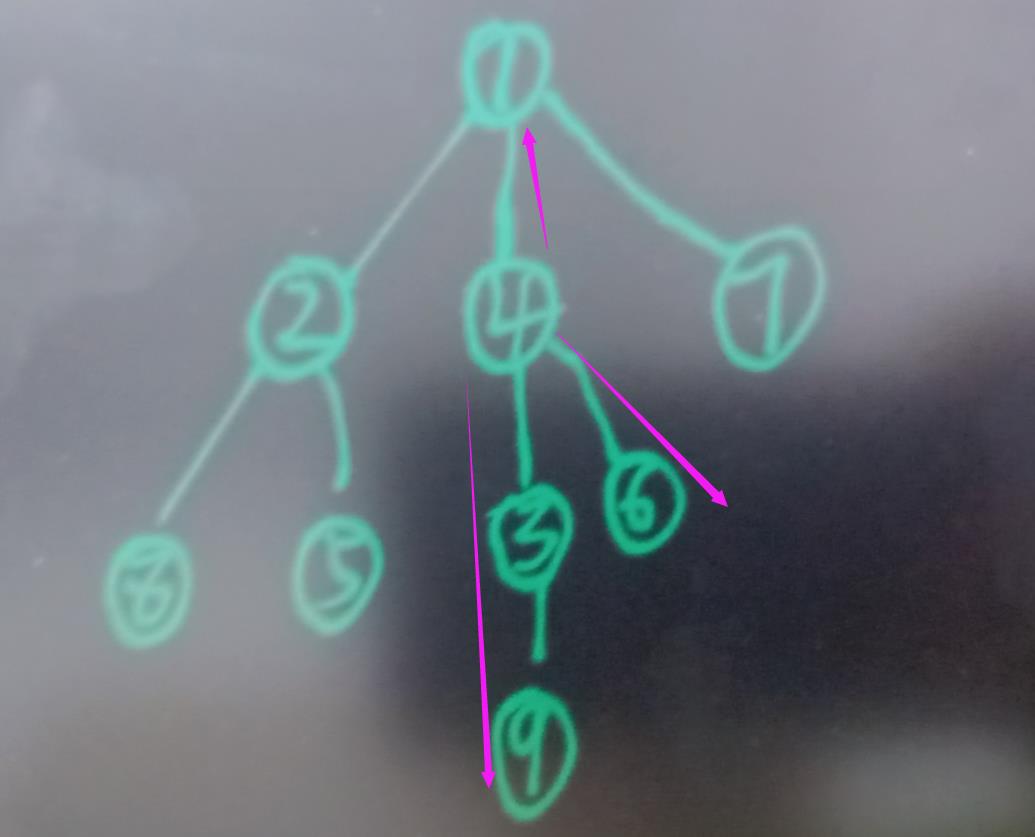
刚开始 4可以到的有 1 3 6
然后1 没有走过，就求去掉1后的最大点数 ， 1又可以到达 2 7 以此递归。
3
6

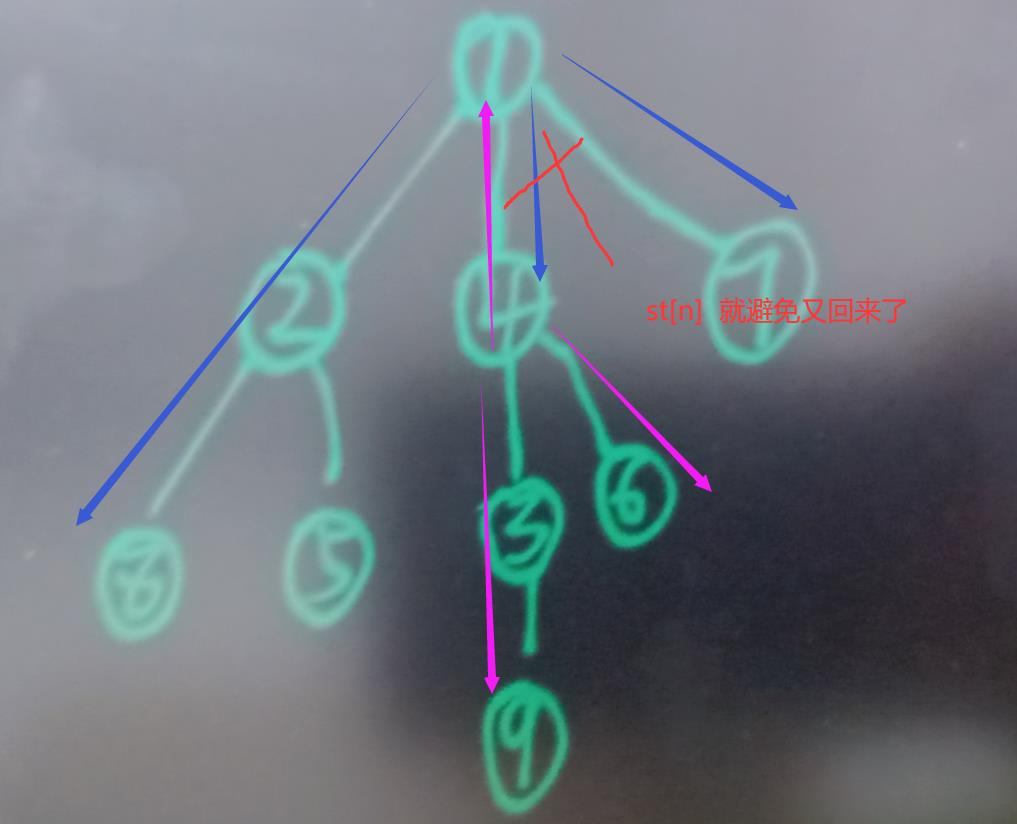
我想 st[ N ] 的作用大家都知道了吧。