数据结构1-4图的基本应用

Posted 2021-05-14 幽殇默

目录

• P5318 【深基18.例3】查找文献 【图的两种遍历】
• P1807 最长路
• P2853 [USACO06DEC]Cow Picnic S 【思路很好】

P5318 【深基18.例3】查找文献 【图的两种遍历】

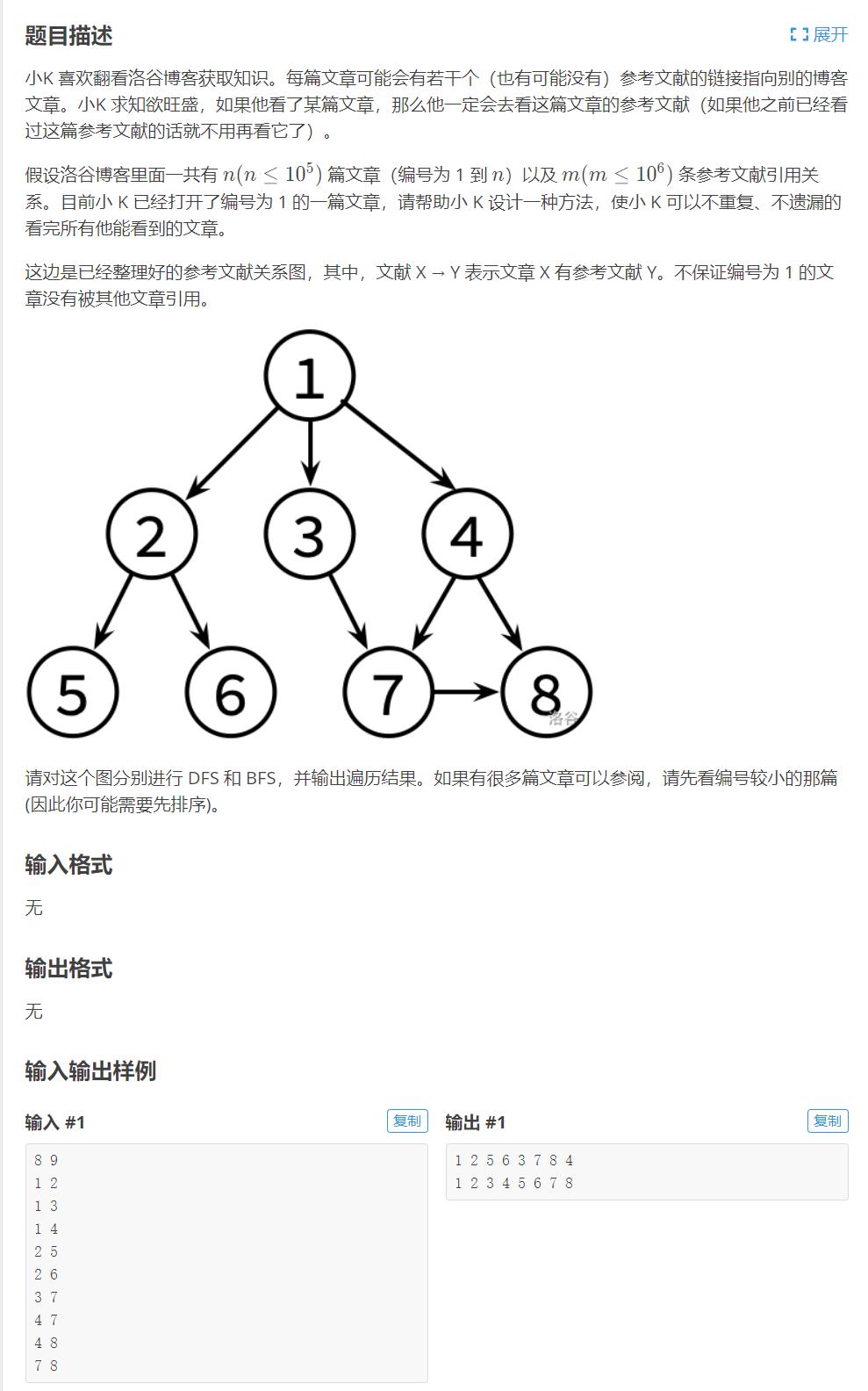
https://www.luogu.com.cn/problem/P5318

#include<cstdio>
#include<iostream>
#include<cstring> 
#include<algorithm>
#include<queue>
using namespace std;
const int N=1e5+10;
const int M=1e6+10;
int h[N],e[M],ne[M],idx;
bool st[N];
int n,m;
struct node
{
	int a,b;
}Node[M];
bool cmp(node a,node b)
{
	if(a.a==b.a)
		return a.b>b.b;
	return a.a<b.a;
}
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
	st[u]=true;
	cout<<u<<" ";
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int j=e[i];
		if(!st[j])
		{
			dfs(j);
		}
	}
}
void bfs(int u)
{
	queue<int> q; q.push(u);
	while(q.size())
	{
		int  t=q.front();  q.pop();
		if(st[t]) continue;
		st[t]=true;
		cout<<t<<" ";
		for(int i=h[t];i!=-1;i=ne[i])
		{
			int j=e[i];
			if(!st[j])
			{
				q.push(j);			
			}
		}
	}
}
int main(void)
{
	cin>>n>>m;
	memset(h,-1,sizeof h);
	for(int i=0;i<m;i++)  cin>>Node[i].a>>Node[i].b;
	sort(Node,Node+m,cmp);//排序
	for(int i=0;i<m;i++) add(Node[i].a,Node[i].b);
	dfs(1); cout<<endl;
	memset(st,0,sizeof st);
	bfs(1); cout<<endl;
	return 0;
}

P1807 最长路

https://www.luogu.com.cn/problem/P1807
Bellman-Ford算法：

#include<cstdio> 
#include<iostream>
#include<cstring>
using namespace std;
const int N=1510;
const int M=5*1e5+10;
struct edge
{
	int a,b,w;
}edges[M];
int dist[N],backup[N];
int n,m; 
int bellman_ford()
{
	memset(dist,-0x7f,sizeof dist);
	dist[1]=0;
	
	for(int i=0;i<n;i++)
	{
		memcpy(backup,dist,sizeof dist);
		for(int j=0;j<m;j++)
		{
			int a=edges[j].a,b=edges[j].b,w=edges[j].w;
			dist[b]=max(dist[b],backup[a]+w);
		}
	}
	
	if (dist[n] <  -0x7f7f7f7f / 2) return -1;
    return dist[n];
}
int main(void)
{
	cin>>n>>m;
	for(int i=0;i<m;i++)
	{
		int a,b,w;
		scanf("%d%d%d",&a,&b,&w);
		edges[i].a=a;
		edges[i].b=b;
		edges[i].w=max(w,edges[i].w);
	}
	cout<<bellman_ford()<<endl;
	return 0;
}

floyd()算法:

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1510;
const int INF=-0x7f7f7f7f;
int d[N][N];
int n,m;
int floyd()
{
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(d[i][k]!=INF&&d[k][j]!=INF)
				d[i][j]=max(d[i][j],d[i][k]+d[k][j]);
			}
		}
	}
	return d[1][n];
}
int main(void)
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(i==j) d[i][j]=0;
			else d[i][j]=INF;
			
	for(int i=0;i<m;i++)
	{
		int a,b,c; cin>>a>>b>>c;
		d[a][b]=max(d[a][b],c);
	}
	if(floyd()== INF ) cout<<-1<<endl;
	else cout<<d[1][n]<<endl; 
	return 0;
}

P2853 [USACO06DEC]Cow Picnic S 【思路很好】

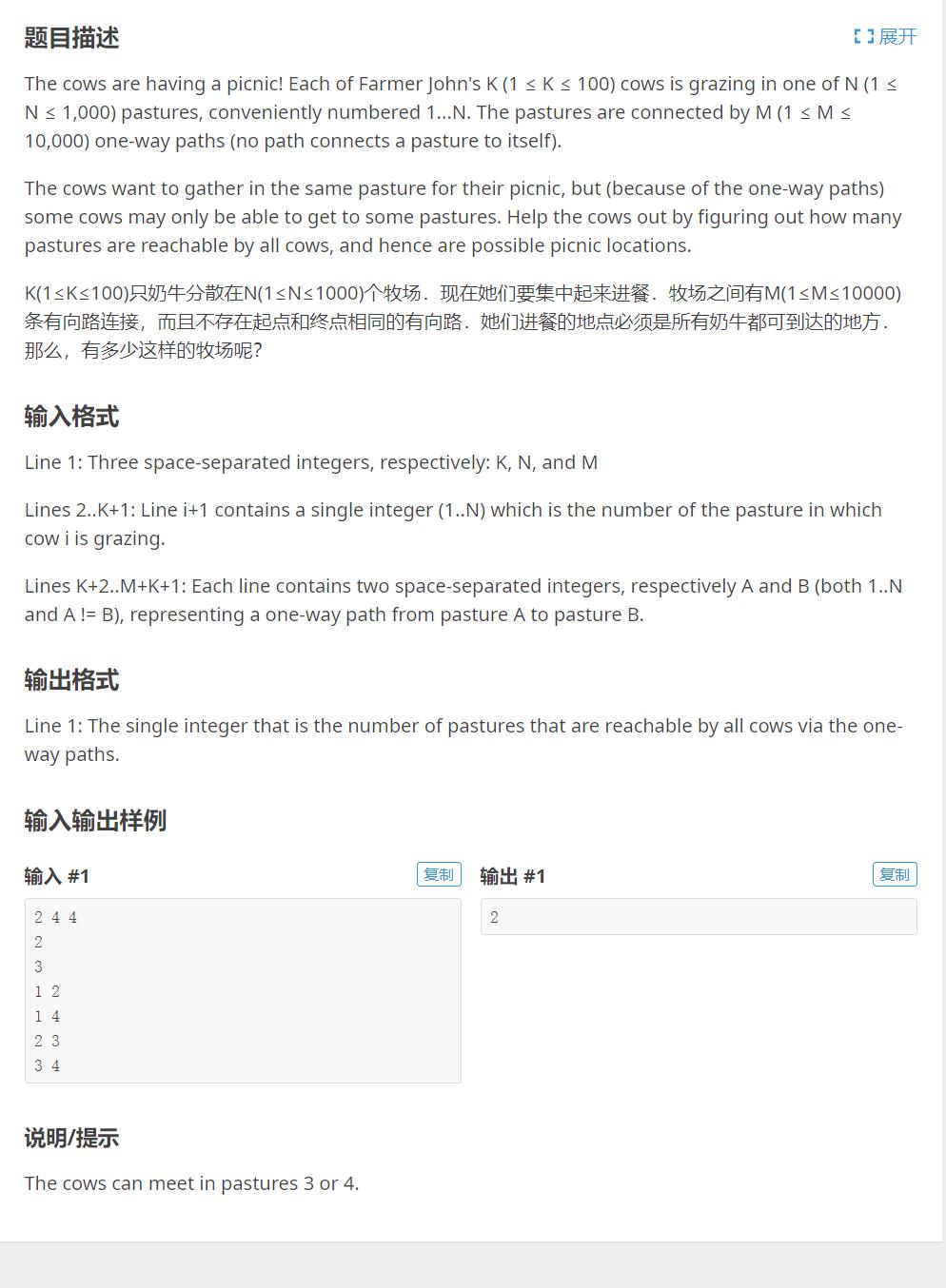
https://www.luogu.com.cn/problem/P2853

思路: 枚举每一个奶牛，记录到达牧场的次数。如果一个牧场的次数等于k说明每一个奶牛都可以来。

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e3+10;
const int M=1e4+10;
int h[N],e[M],ne[M],idx;
bool st[N];
int cnt[N];
int a[105];
int k,n,m;
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
	st[u]=true;
	cnt[u]++;
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int j=e[i];
		if(!st[j])
		{
			dfs(j);
		}
	}
}
int main(void)
{
	cin>>k>>n>>m;
	memset(h,-1,sizeof h);
	for(int i=0;i<k;i++) cin>>a[i];
	while(m--)
	{
		int a,b; cin>>a>>b;
		add(a,b);
	}
	for(int i=0;i<k;i++) 
	{
		memset(st,0,sizeof st);
		dfs(a[i]);
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		if(cnt[i]==k) ans++;
	}
	cout<<ans<<endl;
	return 0;
}