848. 有向图的拓扑序列详解

Posted 2021-05-14 幽殇默

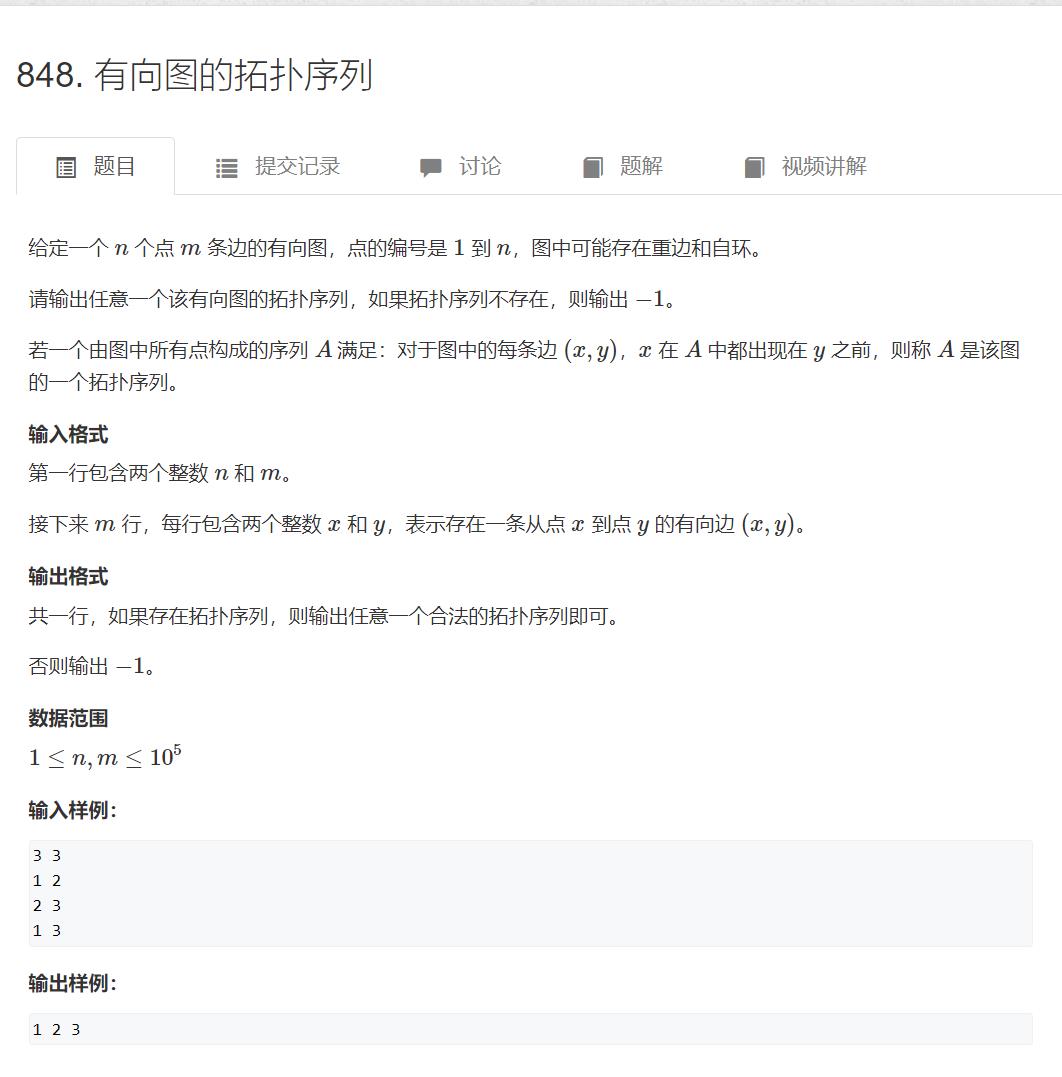
https://www.acwing.com/problem/content/850/

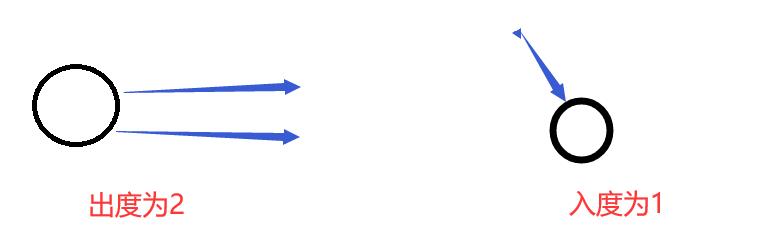
有向无环图(拓扑图) 一定存在一个拓扑序列，
有环图，一定不存在拓扑序列
有拓扑排序就一定是无环的，有环就一定没有拓扑排序。因此可以通过拓扑排序来判断一个有向图是否有环。
因为有环就没法将环中的点存进队列，没有入度为0的点可以进行突破。

---

---

第一步: 首先入度为零的点，可以作为一个起点。 故将其入队

第二步: 遍历所有的入度为零的节点，将其所连的节点的入读减1，如果减后入读为零，则可以入队。

第三步: 如果每一个点都入过队，说明其是一个拓扑序列。

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10;
int n,m;
int h[N],e[N],ne[N],idx;
int q[N],d[N];
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool topsort()
{
    int hh=0,tt=-1;
    for(int i=1;i<=n;i++) if(!d[i]) q[++tt]=i;
    while(hh<=tt)
    {
        int t=q[hh++];
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(--d[j]==0)
            {
                q[++tt]=j;
            }
        }
    }
    return tt==n-1;  //队列是下标是从0开始的
}
int main(void)
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++)
    {
        int a,b; cin>>a>>b;
        add(a,b);
        d[b]++;
    }
    if(topsort())
    {
        for(int i=0;i<n;i++) cout<<q[i]<<" ";
        cout<<endl;
    }
    else puts("-1");
    return 0;
}

拓扑排序入门（真的很简单）