解题报告（十七）概率与期望（概率论）（ACM / OI）

Posted 2021-05-13 繁凡さん

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了解题报告（十七）概率与期望（概率论）（ACM / OI）相关的知识，希望对你有一定的参考价值。

繁凡出品的全新系列：解题报告系列 —— 超高质量算法题单，配套我写的超高质量题解和代码，题目难度不一定按照题号排序，我会在每道题后面加上题目难度指数（ $\\sim 5$ ），以模板题难度 $1$ 为基准。

这样大家在学习算法的时候就可以执行这样的流程：

阅读我的【学习笔记】 / 【算法全家桶】学习算法 $\\Rightarrow$ 阅读我的相应算法的【解题报告】获得高质量题单 $\\Rightarrow$ 根据我的一句话题解的提示尝试自己解决问题 $\\Rightarrow$ 点开我的详细题解链接学习巩固（好耶）

解题报告系列合集：【解题报告系列】超高质量题单 + 题解（ICPC / CCPC / NOIP / NOI / CF / AT / NC / P / BZOJ）

本期题单前置知识：【学习笔记】《概率与期望全家桶》（ACM / OI）概率与期望知识小结

概率

A. UVA11722 Joining with Friend（几何概型）

Problem

两人会面，第一个人去的时间在[t1, t2]中，第二个人去的时间在[s1, s2]中，两人会面成功的话，到达会面地点的时间差不能大于w，求两人成功会面的概率。

Solution

设 $a$ 在 $x$ 时间到达， $b$ 在 $y$ 时间到达，即 $∣ y - x ∣ < = w$ 时可以碰面。即 $x - w < = y < = x + w$

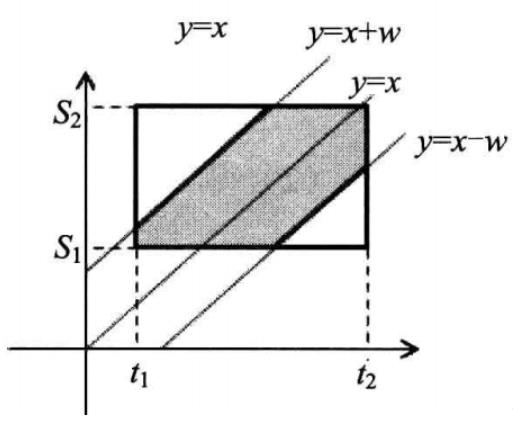
在这里插入图片描述

显然答案就是总面积减去阴影面积。

我们设上面的白色面积为s1，中间阴影面积s2，下面白色面积为s3，则概率为 $\\cfrac{s2}{s1+s2+s3}=\\cfrac{(s2+s1)-s1}{s1+s2+s3}$

即我们可以直接计算直线 $y = x + w, y = x - w$ 切割的四边形上面交的面积，相减即可。

根据四边形形状长度的不同，直线 $y = x + w, y = x - w$ 与四边形的交一共有六种情况：

在这里插入图片描述
分类讨论即可。

Time

$O (1)$

Code

// Problem: UVA11722 Joining with Friend
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA11722
// Memory Limit: 0 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>

using namespace std;

const int N = 50007;

int n, m, t;
double s1, s2, t1, t2, w;
int kcase;

double get_area(double b)
{
	if(t1 + b >= s2) return 0;
	if(t2 + b <= s1) return (t2 - t1) * (s2 - s1);
	if(t1 + b >= s1 && t2 + b <= s2) return (t2 - t1) * (s2 - t2 - b + s2 - t1 - b) * 0.5;
	if(t1 + b >= s1 && t2 + b > s2) return (s2 - b - t1) * (s2 - b - t1) * 0.5;
	if(t1 + b <= s1 && t2 + b >= s2) return (s2 - s1) * (s1 - b - t1 + s2 - b - t1) * 0.5;
	if(t1 + b < s1 && t2 + b < s2 && t2 + b > s1) return (t2 - t1) * (s2 - s1) - (t2 + b - s1) * (t2 + b - s1) * 0.5;
	return 0;
}

void solve()
{
	scanf("%lf%lf%lf%lf%lf", &t1, &t2, &s1, &s2, &w);
	printf("Case #%d: ", ++ kcase);
	double tot = (t2 - t1) * (s2 - s1);
	double up = get_area(-w) - get_area(w);
	printf("%.8f\\n", up / tot);
}

int main()
{
	scanf("%d", &t);
	while(t -- ) {
		solve();
	}
	return 0;
}

B. UVA11021 Tribles（概率DP）

Weblink

https://www.luogu.com.cn/problem/UVA11021

Problem

一开始有 $k$ 个麻球，所有麻球只能活 $1$ 天，死的时候有 $p_i$ 的概率产生 $i$ 只这种麻球（也只能活一天， $0\\le i< n$ ），询问 $m$ 天内所有麻球都死的概率（包括m天前死亡的情况）

Solution

显然每个麻球是相互独立的，我们可以设 $f [i]$ 表示一个麻球第 $i$ 天以内死光的概率，则 $k$ 个麻球在第 $i$ 天内死亡的概率是 $f[i]^k$ 。

我们现在仅考虑一只麻球的情况，即该麻球第一天繁衍多少个，它们在接下来的 $i - 1$ 天内死绝了。

根据全概率公式

$P(A)=\\sum_{i=1}^{n}P(A|B_i)\\times P(B_i)$

我们就可以设计转移方程：

$f[i]=\\sum_{j=0}^{n-1}p[j]f[i-1]^j$

对于每一个麻球来说都有 $n$ 种选择。其中 $p_{j}(f_{i-1})^{j}$ 的表示，生了 $j$ 个麻球，这些麻球在 $i - 1$ 天内死光，即第一只 $a$ 及其后代需要在 $i$ 天内死光，那么第一只的直系后代 $b$ 及其后代需要在 $i - 1$ 天内全部死光，因为第一只需要活一天，则 $b$ 的直系后代及其后代需要在 $i - 2$ 天全部死光（ $b$ 需要活了一天），即 $f [i]$ 由 $f [i - 1]$ 转移过来， $f [i - 1]$ 由 $f [i - 2]$ 转移过来。

因为 $k$ 只麻球相互独立，对于两个独立事件 $A, B$ ， $P(AB)=P(A)\\times P(B)$

最后的答案就是 ${f[m]}^{k}$

CF749E Inversions After Shuffle 解题报告 (期望树状数组)

51nod.1381硬币游戏（概率与期望）

51nod 1639概率与期望绑鞋带

解题报告（十七）概率与期望（概率论）（ACM / OI）

目录

概率

A. UVA11722 Joining with Friend（几何概型）

B. UVA11021 Tribles（概率DP）