搜索二叉树--C++

Posted 小羊教你来编程

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了搜索二叉树--C++相关的知识，希望对你有一定的参考价值。

在这里插入图片描述

搜索二叉树

目录:

一.概念

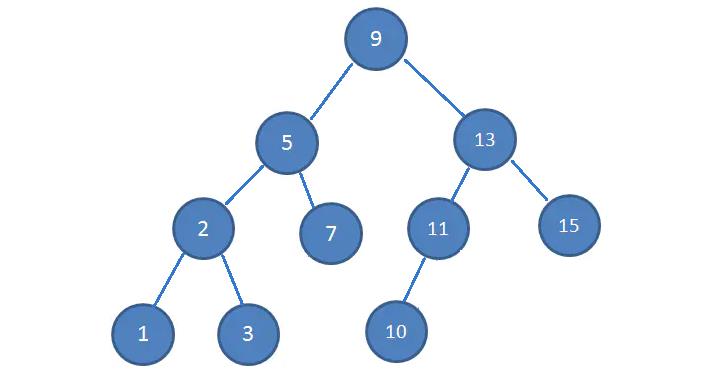
二叉搜索树又称为二叉排序树,或者是一个空树,必须满足以下特点:

满足条件:

1.如果其中的左子树不为空,则左子树上所有的节点的值小于根节点的值
^
2.如果其中的右子树不为空,则右子树上所有的节点的值大于根节点的值
^
3.每个数据都是单一存在,不会重复

在这里插入图片描述

二.接口声明

//1.二叉树内部节点的构建
struct BNode
//2.查找对应的节点
Node* find(const T& val)
//3.拷贝出新的搜索二叉树
Node* copy(Node* root)
//4.插入一个元素
bool insert(const T& val)
//5.删除单一的元素
bool erase(const T& val)
//6.析构函数
~BTree()
//7.中序遍历方式打印
void _inorder(Node* root)

三.接口实现&原理

1.构造内部类

内部写的是所存储的数据和对应的左右子树的存储,包括对每一个节点的构造函数 

template <class T>
struct BNode{

	T _data;					//对应的数据
	typedef BNode<T> Node;		//重命名
	Node* _left;				//左子树的节点
	Node* _right;				//右子树的节点

	BNode(const T& data)		//构造函数
		:_data(data)			//数据的初始化
		, _left(nullptr)		
		, _right(nullptr)		//左右节点初始化成nullptr
	{}
};

2.查找函数

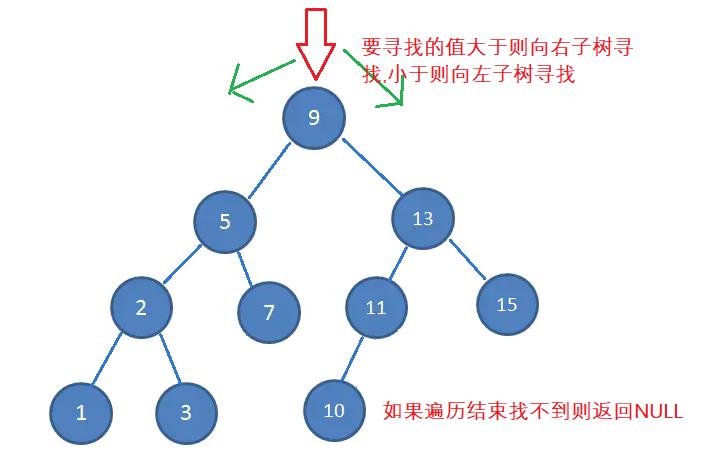
在这里插入图片描述

1.从根节点开始比较大小
^
2.大于向右遍历,小于向左遍历,直到找到对应的值为止. 

	Node* find(const T& val){

		Node* cur = _root;		//创建cur指向其根节点
		while (cur){			//在根节点存在的时候

			if (cur->_data == val)		//如果找到对应的值
				return cur;		//则直接返回
			else if (cur->_data > val)	//如果根节点的值大于要找的值,则更新到左子树进行遍历
				cur = cur->_left;
			else
				cur = cur->_right;		//反之则更新到右子树进行遍历
		}
	}

3.拷贝函数

拷贝构造比较简单,只要开辟出一个新的根节点,然后对其左右子树进行遍历,并且将每个节点进行拷贝 

	Node* copy(Node* root){

		if (root == nullptr)		//如果根节点为空
			return nullptr;			//证明搜索二叉树不存在,直接返回空

		Node* newNode = new Node(root->_data);	//不为空则创建新的Node根节点
		newNode->_left = copy(root->_left);		//对左子树进行遍历,每次遍历拷贝对应的数据
		newNode->_right = copy(root->_right);	//右子树的遍历拷贝
		return newNode;		//最终将拷贝的这个根节点返回
	}

4.插入函数

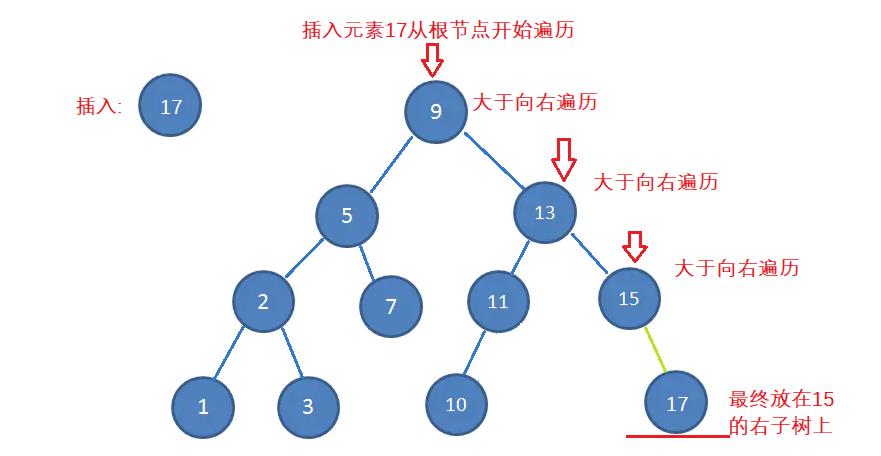
在这里插入图片描述

1.先将插入的数据与根节点比较
^
2.按照方式向对应的子树偏移,最终按照成立的条件进行存放 

	bool insert(const T& val){ //对对应的val值进行插入
		if (_root == nullptr){	//如果根节点为空

			_root = new Node(val);	//则直接将val按照根节点进行创建
			return true;	//返回真
		}

		//搜索找到合适的位置
		Node* cur = _root;		//定义出对应的cur为根节点
		Node* parent = nullptr;		//定义出parent首先为空,是cur的父节点
		while (cur){		//如果cur存在

			parent = cur;		//将父节点放在根节点
			if (cur->_data == val)		//如果插入的数据在二叉树中存在则返回错误
				return false;		//因为搜索二叉树中的数据是单一的
			else if (cur->_data > val)		//如果插入的数据大于这个节点的值,则会向右进行办理
				cur = cur->_left;
			else
				cur = cur->_right;		//反之,小于则向左遍历
		}
		//找到最后对应的那个节点后
		cur = new Node(val);		//利用构造函数对这个节点进行构建
		if (parent->_data > val)	//当对应的根节点的值大于这个要插入的节点的时候	
			parent->_left = cur;		//放在对应的左子树上
		else
			parent->_right = cur;		//反之则放在对应的右子树上

		return true;		
	}

5.删除函数

对于搜索二叉树的删除单个元素这里是比较重要的一个部分,分为四个部分理解代码.

(1)删除的节点是叶子节点

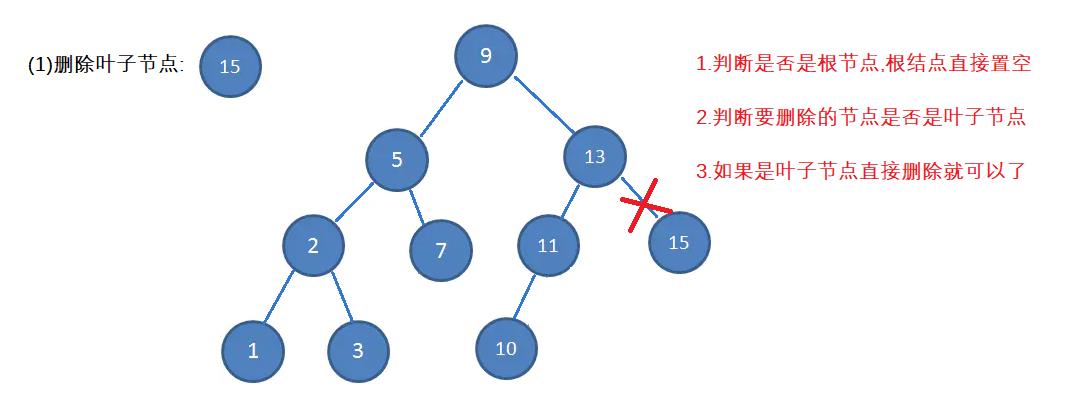
在这里插入图片描述

(2)删除的节点只存在右子树

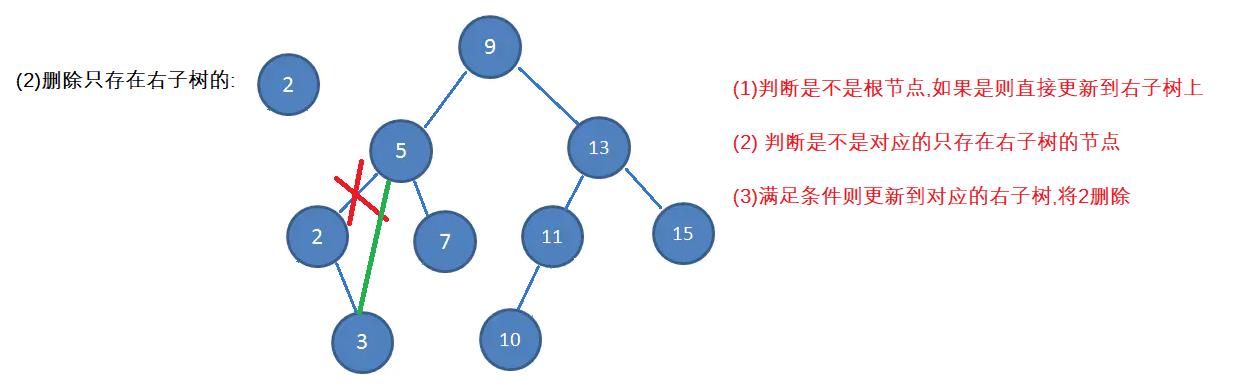
在这里插入图片描述

(3)删除的节点只存在左子树

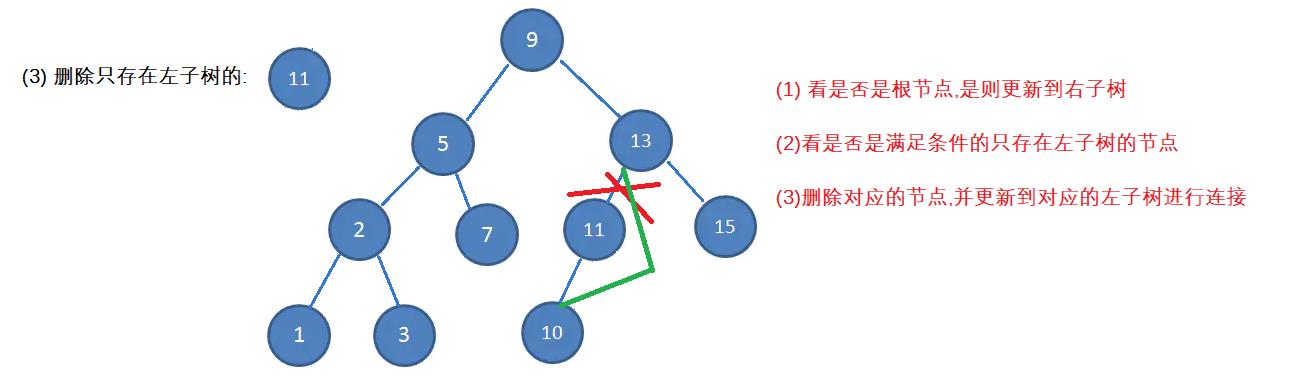
在这里插入图片描述

(4)删除的节点存在左子树和右子树

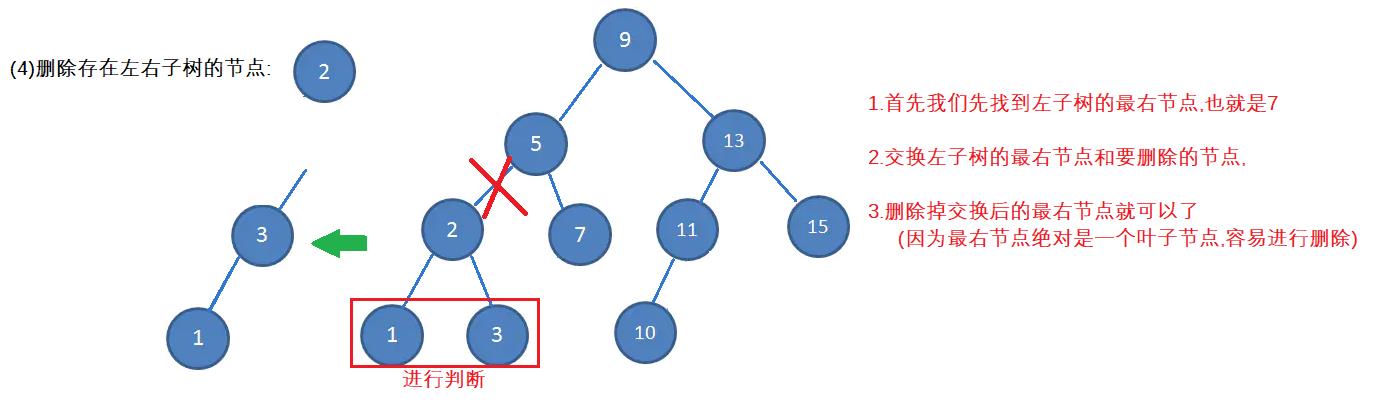
在这里插入图片描述

代码实现:

	bool erase(const T& val){		//布尔值返回真假
		
		//查找
		Node* cur = _root;
		Node* parent = nullptr;		//给定两个指针,分别标明要删除的节点和对应的父节点
		while (cur){	//当存在根节点的时候
			
			if (cur->_data == val)		//找到值则直接返回
				break;
			parent = cur;		//父节点更新
			if (cur->_data > val)		//如果大于对应节点的时候
				cur = cur->_left;		//向左子树遍历
			else
				cur = cur->_right;		//反之则向右子树遍历
		}
		//判断是否找到需要删除的节点
		if (cur == nullptr)		
			return false;		//未找到则返回false

		//删除
		//====================================================1.删除的为叶子节点
		if (cur->_left == nullptr&&cur->_right == nullptr){
			
			//判断是否是根节点
			if (cur == _root){
				
				_root = nullptr;
			}
			else{
				
				//判断需要删除的节点在父节点的那一边
				//判断是否是叶子节点
				if (parent->_left == cur)
					parent->_left = nullptr;
				else
					parent->_right = nullptr;
			}
			//删除节点
			delete cur;
		}

		//====================================================2.删除的存在右子树
		else if (cur->_left == nullptr){
			
			//判断删除是否为根节点
			if (cur == _root){
				
				//更新
				_root = cur->_right;
			}
			else{
				//判断是否满足只存在右子树的条件
				if (parent->_left == cur)
					parent->_left = cur->_right;
				else
					parent->_right = cur->_right;
			}
			//删除节点
			delete cur;
		}
		//====================================================3.删除的存在左子树
		else if (cur->_right == nullptr){
		
			if (cur->_right == _root){		//如果是根节点
				
				_root = cur->_left;		//直接指向对应的左子树
			}
			else{
				//当不为根节点的时候,看是否是满足存在左子树的条件
				if (parent->_left == cur)
					parent->_left = cur->_left;
				else
					parent->_right = cur->_left;
			}
			delete cur;		//删除节点
		}
		
		//====================================================4.删除的节点存在左右子树
		else{
			
			//左右子树都存在
			//1.假设找左子树的最右节点
			Node* leftRightMost = cur->_left;
			parent = cur;

			while (leftRightMost->_right){	//循环找到左子树的最右节点
				
				parent = leftRightMost;
				leftRightMost = leftRightMost->_right;
			}

			//2.交换
			swap(cur->_data, leftRightMost->_data);		//找到后交换要删除的节点和左子树的最右节点

			//3.删除最右节点
			if (parent->_left == leftRightMost)	//满足条件的话
				parent->_left = leftRightMost->_left;
			else
				parent->_right = leftRightMost->_left;
	
			delete leftRightMost;	//然后将交换后的最右节点进行删除
		}
		return true;		//删除成功
	}

6.析构函数

析构函数首先遍历将其每一个对应的节点进行销毁,然后将根节点置空 

	~BTree(){

		if (_root){

			destory(_root);		//调用destory函数
			_root = nullptr;	//将根节点置空
		}
	}

	void destory(Node* root){		//封装函数在析构中调用

		if (root){		//根节点存在

			destory(root->_left);		//依次左子树进行遍历删除
			destory(root->_right);		//右子树遍历删除
			delete root;		//删除根节点
		}
	}

7.利用中序遍历的方式进行打印

中序遍历的方式就是我们先遍历所有的左子树,将其中的数据进行输出,然后再遍历右子树,将数据输出,就得到了对应的顺序数值 

	void inorder(){

		_inorder(_root);	//调用封装的函数
	}

	//搜索树的中序遍历有序
	void _inorder(Node* root){

		if (root){	//存在根节点

			_inorder(root->_left);		//先遍历左子树进行打印
			cout << root->_data << " ";	//输出对应的数据
			_inorder(root->_right);		//遍历右子树输出数据
		}
	}

四.性能分析

插入和删除操作都必须进行先查找,查找的效率代表了各个操作的性能.

最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：log2N
最差情况下，二叉搜索树退化为单支树，其平均比较次数为：N/2

对于搜索二叉树主要理解它内部不会存在重复的元素.还有就是对于erase成员函数的四种情况的考虑.

以上是关于搜索二叉树--C++的主要内容，如果未能解决你的问题，请参考以下文章

怎么判断是不是是完全二叉树 用C++或C语言

C ++在不同类型的二叉树中搜索二叉树

Cuda C中的二叉树搜索 - 并行

⭐算法入门⭐《二叉树 - 二叉搜索树》简单02 —— LeetCode 98. 验证二叉搜索树

⭐算法入门⭐《二叉树 - 二叉搜索树》简单07 —— LeetCode 530. 二叉搜索树的最小绝对差

c_cpp 二分搜索是所有以比较为基础的搜索算法时间复杂度最低的算法。用二叉树描速二分查找算法，最坏情况下与二叉树的最高阶相同。比较二叉树线性查找也可用二叉树表示，最坏情况下比较次数为数组元素数量。任