案例学习——Unity基于体绘制的大气散射shader

Posted 清清！

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了案例学习——Unity基于体绘制的大气散射shader相关的知识，希望对你有一定的参考价值。

本案例学习资料来源
Volumetric Atmospheric Scattering

案例学习——Unity基于体绘制的大气散射shader

0 效果展示

先看看实现的效果（米氏散射和瑞利散射结合的地球大气+云层+地球昼夜）
在这里插入图片描述
在这里插入图片描述

1 引入

抬头望天，我们会发现天空经常是蓝色
在这里插入图片描述
日出日落时天空经常会是红色
在这里插入图片描述
这样的光学现象主要是光进行了瑞利散射（Rayleigh scattering），本文依照AlanZucconi大神的教程，介绍如何对大气散射进行数学建模，来重现这些大气中的视觉效果。

1.0 介绍

对于传统的渲染技术，会假设物体是一个空的外壳，我们在外壳表面即可进行所有效果的计算。这种简化方式对于渲染物体表面来说是很高效的。

但是有些效果是由于光穿透了物体才能实现的，比如半透明物体正是如此。不过聪明的人们也研究了一些快速近似半透明物体的方法（GDC 2011 – Approximating Translucency for a Fast, Cheap and Convincing Subsurface Scattering Look）。

但是大气就很难这么做了，因为天空并不是一个“物体”，我们不能只是渲染表面的壳，我们还需要模拟光线在大气中到底经历了什么。

不光光渲染壳，同时也要渲染物体内部的光线传播，这个技术通常被称为体积渲染/体绘制（volumetric rendering），在本文的上一篇文章做出过一些小的探讨（比如光线步进和有向距离函数）。

不过仅是这样还不足以模拟大气散射，接下来会介绍一种更合适的方法，被称为体积单次散射（volumetric single scattering）。

1.1 单次散射（Single Scattering）

在游戏引擎的基本光照模型实现中，都假设光线在真空中传播，所以物体的表面属性往往是影响光照的唯一因素。

然而在物理上，传播媒介对光的影响也是很重要的，对于大气来说，穿过的空气多少或者空气的成分就很能影响光照的效果。

在图形学进行大量的简化之后，空气影响我们感知光线的方式，通常会分为两种，分别是出射散射（Out-Scattering）和入射散射（In-Scattering）

1.1.1 出射散射（Out-Scattering）

出射散射也就是光子打中空气分子后被，原本要射向摄像机的光线进行了偏转，光线的方向进行了改变。
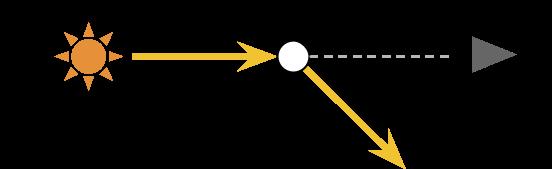
在这里插入图片描述
对于一个大光源来说，能够发射出很多很多光子，因而在空气中传播时经常会发生出射散射。
空气密度越大，光线传播的距离越长，出射散射发生的光线偏转越多，对光线的削弱效果越明显。
在这里插入图片描述

1.1.2 入射散射

与出射散射相反，本来不指向相机的光线也可能被偏转到相机的方向，这就是入射散射。
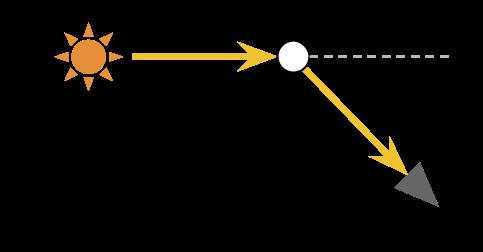
在这里插入图片描述
入射散射允许相机看到不在可视范围内的光源，比较明显的例子就是光晕，比如下图由于Particle的偏转，会让人觉得沿着视线和Particle的连线处有光线，看起来也就是光晕。
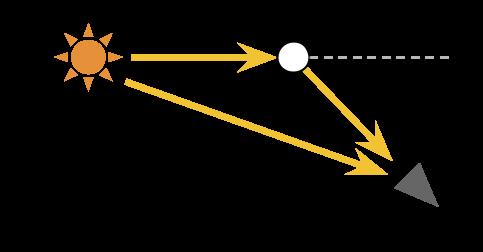
在这里插入图片描述

1.2 基于体绘制的单次散射模型（Volumetric Single Scattering）

光线在实际传播当中会偏转很多次，就像下图这样
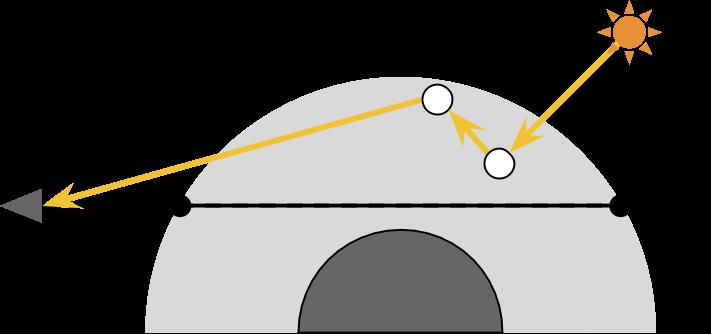
在这里插入图片描述
但是高度的仿真是光线追踪的内容，对于本文来说，我们只考虑单次散射——即光线从太阳发出过、只经过一次散射被改变方向后射入我们的眼睛。

对于渲染一个行星的大气，我们会逐步构建一个模型，首先我们考虑相机
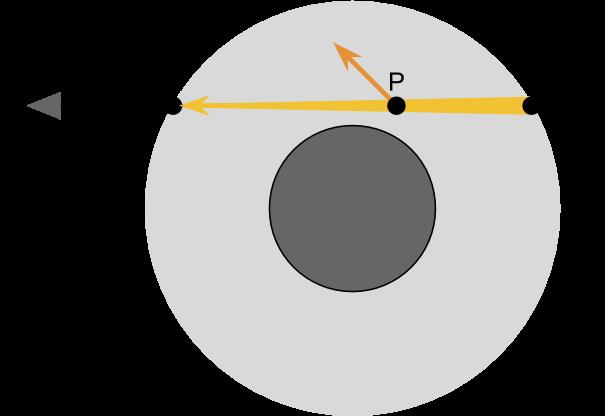
在这里插入图片描述

  • 摄像机的视线从A处进入大气，经过B处
  • 我们计算光线从B到A的过程中是如何受到散射影响的，也就是计算在AB光路上每一个位置P造成的出射散射的衰减贡献&入射散射的叠加贡献

该模型中也存在光源的贡献，我们通常假设是太阳的光线经过入射散射的偏转会让我们看见
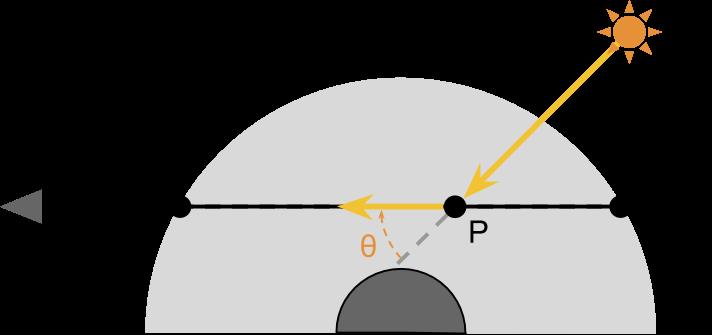
在这里插入图片描述
太阳在照射到P的过程中也存在出射散射
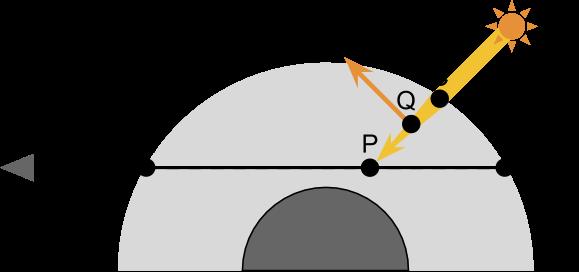
在这里插入图片描述
总结这些部分，混合在一起，也就是如下的样子
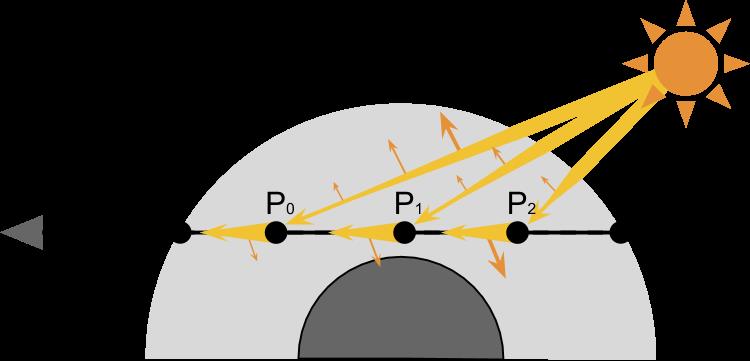
在这里插入图片描述

  • 相机的视线从A进入，经过行星大气，看到B
  • 我们需要去计算AB段上每一点P的散射贡献
    • P点接受的光线都来自于太阳
    • P点接受的光线进入大气层时会受到出射散射的影响
    • P点接受的光线经过入射散射偏转进入摄像机，在射向摄像机的图中又会经过出射散射偏离

2 大气散射背后的理论

2.1 透射函数

为了计算传入相机的光线有多少，我们可以先考虑一段光线，如下图所示
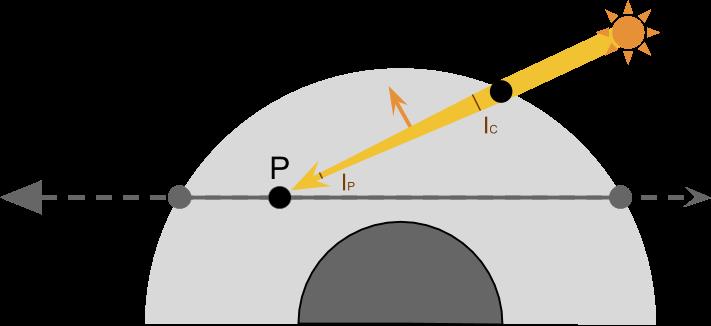
在这里插入图片描述

  • 光线从太阳传到C，此时是真空，所以没有损失，我们用 I C I_C IC​指代C点的光强
  • 在从C到P的过程中，经过出射散射，光强会衰减，我们用 I P I_P IP​指代P点的光强
  • I P I_P IP​比 I C I_C IC​的值也就是透射率（transmittance） 。
  • 透射率 T T T表示在某段路径上的对光照的衰减程度。 T ( C P ‾ ) = I P I C T(\\overline{CP})=\\frac{I_P}{I_C} T(CP)=IC​IP​​
  • 对于某一个值的透射率 T T T，P点的光强也就是 I P = I C ∗ T ( C P ‾ ) I_P=I_C*T(\\overline{CP}) IP​=IC​∗T(CP)

2.2 散射函数

P点在接受光照后，又会因为散射偏转一部分，于是为了计算有多少光能从P进入视野，我们需要散射函数 S S S来表示某一方向上光线的偏转情况。

如下图，那些偏转了 θ θ θ角的光线被指向了A点的摄像机.
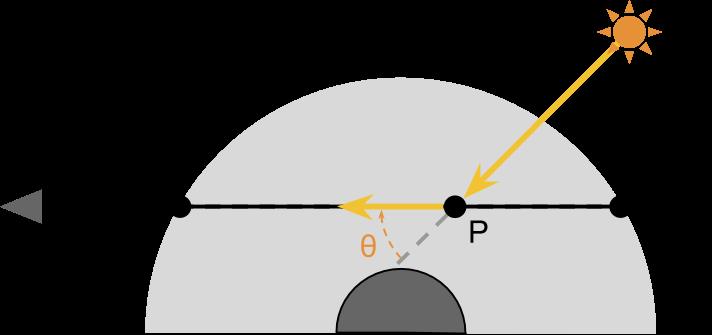
在这里插入图片描述
我们用 S ( λ , θ , h ) S(λ,θ,h) S(λ,θ,h)的值来代表发生了 θ θ θ度偏转的光线比重。

λ λ λ代表光线的波长， θ θ θ是偏转角度， h h h是P点的离地高度（高度会影响大气密度，密度会影响散射程度）

于是我们可以得到从P点出发到A点的光强了
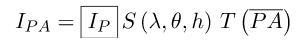
在这里插入图片描述
带入之前求出的 I P = I C ∗ T ( C P ‾ ) I_P=I_C*T(\\overline{CP}) IP​=IC​∗T(CP)
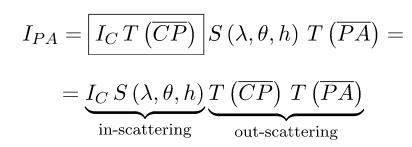
在这里插入图片描述
整个过程再次回忆一下是这样

  • 光从太阳进入 C C C点，真空中无影响
  • 从 C C C点进入大气传到 P P P点，受到出射散射影响只有占比 T ( C P ‾ ) T(\\overline{CP}) T(CP)的光线到达了 P P P点
  • P P P点的光线被入射散射偏转到摄像机中，偏转比率是 S ( λ , θ , h ) S(λ,θ,h) S(λ,θ,h)
  • 偏转完成后，从 P P P到 A A A，受到出射散射影响只有占比 T ( P A ‾ ) T(\\overline{PA}) T(PA)的光线到达了 A A A点

2.3 数值积分

I P A I_{PA} IPA​是代表从 P P P点到 A A A点的光强，而 A A A点的所有光强是无数个 P P P点叠加起来的
I A I_A IA​是所有 P ∈ A B ‾ P∈\\overline{AB} P∈AB的贡献之和
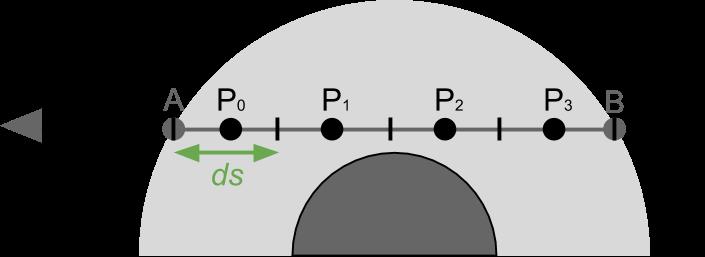
在这里插入图片描述
我们可以近似看成数值积分的形式把AB这一段加在一起
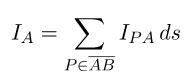
在这里插入图片描述
在大气shader中，我们遍历若干个大气的点 P i P_i Pi​累计贡献

2.4 方向光

因为太阳离我们很远，所以我们可以假设太阳光是方向光，所有在AB线上的点P接受的光都是来自同一个方向。
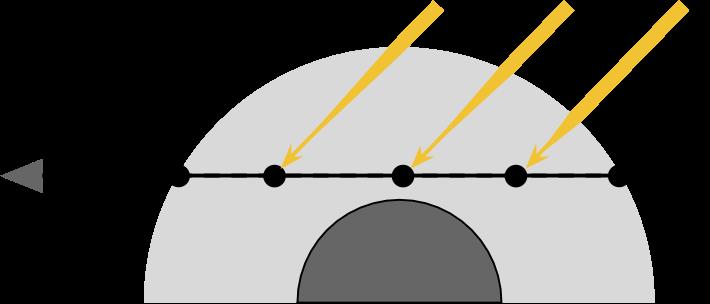
在这里插入图片描述
之前对于某一个 C C C点入射的光强我们定义是 I C I_C IC​，那么我们可以将所有 I C I_C IC​都看成是一个常量 I S I_S IS​
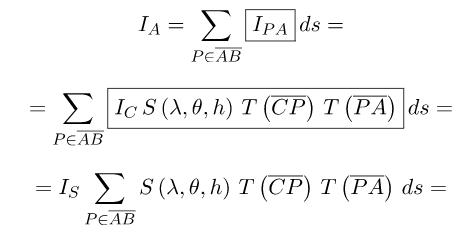
在这里插入图片描述
另外，如果入射光的方向都相同，其实 S ( λ , θ , h ) S(λ,θ,h) S(λ,θ,h)中的 θ θ θ也是一个常数，之后会进行讨论

2.5 吸收系数

光线和空气分子的相互作用除了偏转还有吸收，有些波长被吸收于是大气会呈现出某些独特的颜色。
我们在实现中会忽视吸收系数的影响，用其他的方式给大气调色。

3 瑞利散射中的数学

在之前的两节中，我们得到一个用于在shader中近似重现大气散射的框架公式，我们需要在框架的基础上更进一步。

光和物质的作用非常复杂，对于大气散射的建模是比较困难的，因此我们有许多特定的散射模型用于各种各样的情况。

比如通过考虑 瑞利散射（Rayleigh Scattering） 和 米氏散射（Mie Scattering） ，我们可以重现行星大气的大多数效果。

瑞利散射用来进行小分子的建模，比如氧分子和氮分子。

  • 小分子指大小远小于光线波长的粒子。这些分子大小比波长还要小很多，因此光的波长也会影响Rayleigh散射的程度。

米氏散射用来进行大小远大于光线波长的粒子的建模，比如花粉，灰尘。

  • 大粒子在发生散射的时候会把更多的光散射到前向，因此我们认为Mie散射跟光线波长无关。

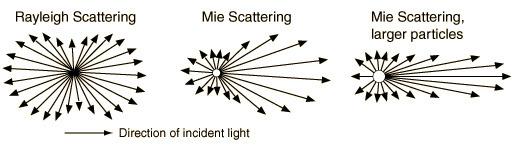
在这里插入图片描述
瑞利散射导致蓝天与红色的日出日落，米氏散射使得云彩变成白色。

我们需要深入了解一下它们。

3.1 瑞利散射概念

对于足够小的粒子，光线在撞击它后会经历什么？我们通常使用瑞利散射来建模。
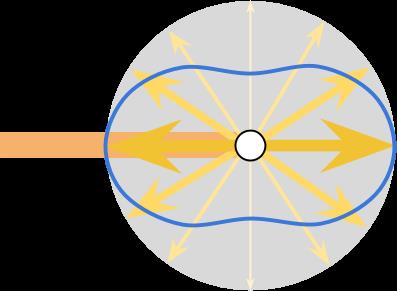
在这里插入图片描述
其效果如图所示，一部分光线不受影响，一小部分散射到四面八方，蓝色的萧条表示了每个方向的散射分布情况。

我们可以用瑞利散射的方程，也就是之前的散射函数 S ( λ , θ , h ) S(λ,θ,h) S(λ,θ,h)去描述这一现象

对于光线 I 0 I_0 I0​，对于某方向 θ θ θ的散射比例为
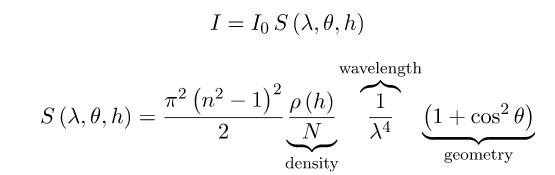
在这里插入图片描述

其中的参数如下：

  • λ λ λ：入射光的波长
    θ θ θ：散射角度
    h h h：散射点的高度，为0时体现海平面附近的散射情况
    n = 1.00029 n=1.00029 n=1.00029 代表空气折射率
    N = 2.504 ∗ 1 0 25 N=2.504*10^{25} N=2.504∗1025 代表标准大气分子数的密度，单位是分子数/立方米
    ρ ( h ) ρ(h) ρ(h)：密度比，海平面时该值为1，以h为指数递减，后续会进行讨论
  • 这并不是真正的瑞利散射方程，如果去百科上查，可能发现公式和这个是截然不同的
    本文的公式来自于该论文Display of The Earth Taking into Account Atmospheric Scattering
    可以配合文章里的一幅图理解一下上面的公式
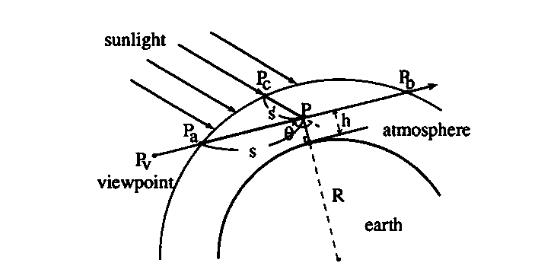
    在这里插入图片描述
  • 这个结果怎么推导出来的？在此不多阐述
    可以看看文章（反正拿了结果就好（x
    那为什么会以蓝线这样的形状散射呢？
    瑞利散射的实质并不是真的因为光和粒子发生了“碰撞”。
    光是一种电磁波，它与某些粒子中本来就存在的电荷不平衡相互作用。大气中的分子在入射光电矢量作用下会极化，从而产生偶极辐射。

对于瑞利散射，我们主要关注几个问题
一是它的散射方向，呈现两瓣的样子
二是散射的光强取决于入射光的波长 λ λ λ
下图展示了三个波长的 S ( λ , θ , h ) S(λ,θ,h) S(λ,θ,h)（h=0）
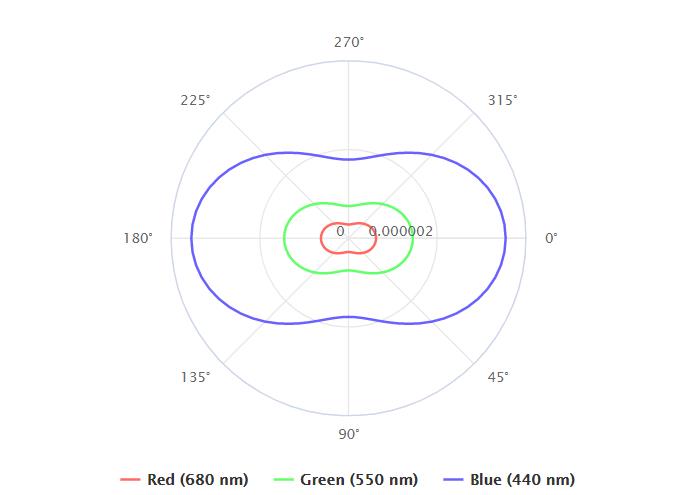
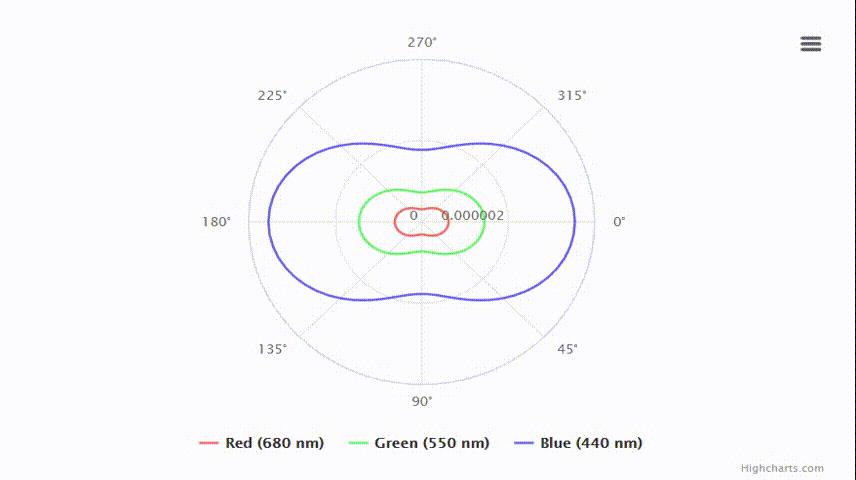
在这里插入图片描述
在这里插入图片描述
下面这张图展示了可见光谱各个连续波长的 S ( λ , θ , h ) S(λ,θ,h) S(λ,θ,h)渲染情况（黑色为不可见光），该效果在ShaderToy可以找到
在这里插入图片描述

3.1.1 瑞利散射系数

瑞利散射的公式 S ( λ , θ , h ) S(λ,θ,h) S(λ,θ,h) 表示在某个特定的方向上的有多少光

但是并没有说在这个位置上整体的能量情况，是少了还是不变，少了的话少了多少，所以我们需要算一下。

我们对瑞利散射的 S ( λ , θ , h ) S(λ,θ,h) S(λ,θ,h) 做球面积分，得到总散射的能量 β ( λ , h ) β(λ,h) β(λ,h)

以上是关于案例学习——Unity基于体绘制的大气散射shader的主要内容，如果未能解决你的问题，请参考以下文章

程序化天空盒过程记录01：日月 天空渐变 大气散射

图像去雾基于matlab颜色衰减先验图像去雾含Matlab源码 2036期

图像去雾基于matlab颜色衰减先验图像去雾含Matlab源码 2036期

GLSL 大气散射不随变换缩放

大气散射模型的推导过程

大气光散射实现