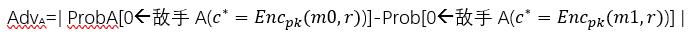公钥加密方案的安全目标

Posted 2021-05-11 Kaladou~

​ 公钥加密方案的安全目标（从低到高，从敌手的角度指攻破安全体制由难到易）：

1、不可攻破性：指抗完全攻破，从敌手攻击的角度而言，指敌手能从公钥得到相应的私钥。所以完全攻破也叫密钥恢复。对公钥加密而言，公钥总是可以得到的，因而抗完全攻破是一种隐含的基本要求。

2、单向性：也叫抗部分攻击，从敌手攻击角度而言称为部分攻破（Partial Break），即明文恢复 ，指敌手可能不知道密钥 （这里指私钥） ， 但对某些密文能直接得到明文。更严格地说，抗部分攻破是指： 在不知道私钥的情况下 ，从密文不能恢复相应的明文，即敌手 A 成功地对加密方案 Enc 求逆的概率是可忽略的

3、密文不可区分性：密文可区分是指攻击者能以超过 1/2 的概率解决下面的问题 ： 给攻击者任意两个明文和其中任意一个明文的密文，攻击者来判断这个密文是两个明文中哪一个明文的密文。

​ 下面就**形式化**的描述密文不可区分性😄

-------->敌手选出的两个等长的明文，加密者随机均匀地选择其中一个进行加密，敌手无法从得到的密文中判断是哪个明文进行了加密，即对任意公钥密码系统 （Gen, Enc, Dec） ，如果敌手的优势概率：
$$〖Adv{〗}_A=Pr[(pk,sk)\leftarrow Gen(1^n),(m0,m1,s)\leftarrow A_1(pk),c=〖Enc{〗}_{p}k(m_b,r):A_2(m0,m1,s,c)=b]-1/2$$
是可以忽略的，则称为密文不可区分性。

​ n表示安全参数（如密钥长度）；

​ 敌手A=(A1,A2) 是一个两阶段攻击者（寻找阶段、猜测阶段）；

​ s 是攻击过程中获得的某些敌手自认为有利攻击的辅助信息；

​ r 是加密算法中使用到的随机数；

​ b 是从 0 或 1中随机选取的；

换种说法就是：

敌手A被告知某个公钥pk，然后进行以下两各阶段：

寻找阶段：敌手A选择两个等长的明文m0、m1，以及自认为有利攻击的辅助信息s；

猜测阶段：敌手被告知其中一个明文和随机数r得加密结果C*，当然这里得b是保密的
$$c0=〖Enc{〗}_{p}k(m0,r)若b=0$$

$$c1=〖Enc{〗}_{p}k(m1,r)若b=1$$

判断C*是c0还是c1。

​ 敌手A的目标是以大于一半的概率猜对b的值【也就是猜对的概率要比猜错的概率大1/2，】：

这个概率是可以忽略的，那么就说c0和c1不可区分。

两阶段中攻击者都拥有访问加密预言机的能力，是否拥有访问解密预言机的能力区分了该方案是 CCA1安全还是 CCA2安全。显然，对于任何确定性的公钥加密，都可以通过向加密预言机问询 m0、 m1的密文来确定 c=Enc(pk,mb) 是否是对 m0或 m1的加密。因此，只有随机化的加密 （也称为概率加密）才可能具有不可区分性。因此，加密算法 Enc(pk,mb,r) 中需要拥有随机数 。

4、不可延展性：从安全角度来讨论，不可延展性是指攻击者无法构造与已给密文相关的新密文。即从给定密文不可以构造一个与给定密文对应明文相关的明文的密文。简言之，从 Enc(m) 不可推出 Enc(R(m))，这里 R 是一个非平凡的关系。NM 安全是 Dolev、Dwork 和 Naor在 1991年提出的。容易理解，不可区分性攻击是判定问题，不可延展性攻击是一个计算问题。

【参考文献】：任伟.可证明安全公钥密码学探究[J].信息网络安全,2011(11):1-4+13.