2021-BNUZ-IT节程序设计竞赛网络赛题解
Posted hexWars
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2021-BNUZ-IT节程序设计竞赛网络赛题解相关的知识，希望对你有一定的参考价值。
文章目录
前言
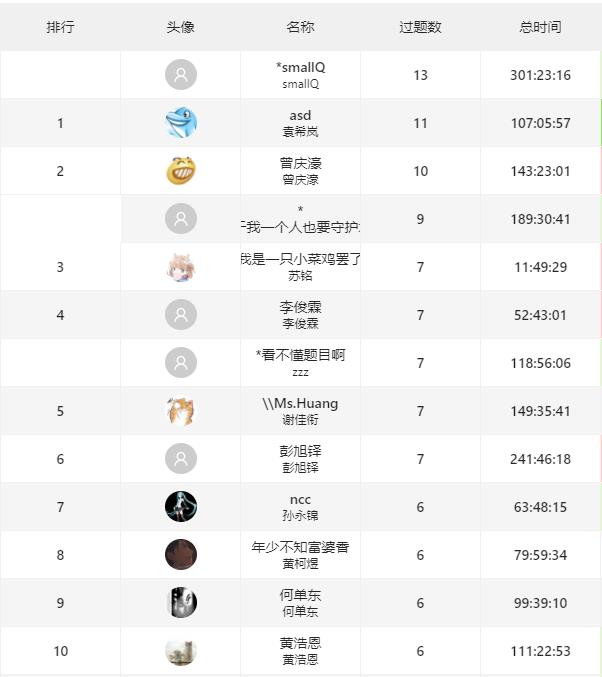
网络赛有效提交者143人(不包括打星选手),题目类型包括数据结构,模拟,动态规划,贪心等算法
让我们来看看排行前十的选手(没错,打星选手就是大佬,学长闲着做了一下直接AK了…)
本次IT节网络赛由某点倾情赞助…就怪
去年是二次元,今年是网文系列
题目名字改编自以下小说
-
快穿之xxx系列(这个太多了)
听说有人觉得插图好看,那就找出题人要照片吧,其实有些图片和题目都没啥关系~
下面给出C++代码
没有学习C++的同学,可以简单把cin看成C语言里的scanf,把cout看成C语言里的printf
我们会根据一定比例挑选进入现场赛的选手,届时将会将名单公布,欢迎关注公众号北师珠ACMICPC,敬请期待
我的徒弟都是实习生
简单组合数学问题
有一点点小坑,如果按照正常算的话会溢出(边界数据阶乘unsigned long long都存不下)
坑就在这里,我们需要的是解决溢出问题,不是时间
看着很少有一发过的人,基本都被出题人坑了一手
#include<iostream>
using namespace std;
typedef long long ll;
ll cb[100001];
//ll C(ll k,ll n){//溢出的做法
// ll a = n-k,b = k;
// if(a>b){//保证a最小
// a^=b^=a^=b;
// }
// if(a==0)return 1;
// ll res = 1;
// for(int i=n ; i>b ; i--){
// res*=i;
// }
// for(int i=2 ; i<=a ; i++){
// res/=i;
// }
// return res;
//}
ll C(ll k, ll n) {//优化
ll a = n - k, b = k;
if (a > b) {//保证a最小
a ^= b ^= a ^= b;
}
if (a == 0)return 1;
ll res = 1;
for (int i = n, j = 1; i > b; i--, j++) {
res *= i;
if (j <= a) {
res /= j;
}
}
return res;
}
int main() {
ll t, n, m;
while (cin >> t >> m >> n) {
ll res = 0;
for (int i = 4; i <= t - 1; i++) {
int man = i;
int girl = t - i;
if (man <= n && girl <= m) {
res += C(man, n) * C(girl, m);
}
}
cout << res << "\\n";
}
}
快穿之我只想测身高
思考：
题目中的M对关系实际上是人之间身高的相对大小关系。具体来说,我们建立一个数组C,数组中起初全为0。若一条关系指明Ai和Bi可以互相看见(不妨设Ai<Bi),则把数组C中下标为Ai+1到Bi-1的数都减去1,意思是在Ai和Bi中间的人,身高至少要比它们小1。因为第P个人是最高的,所以最终C[p]一定为0。其他的人与第P个人的身高差距就体现在数组C中。换言之,最后第i个人的身高就等于H+C[i]。如果我们朴素执行把数组C中下标为Ai+1到Bi-1的数都减去1的操作,那么整个算法的时间复杂度为O(NM),复杂度过高。一个简单而高效的做法是,额外建立一个数组D,对于每对A和B,令D[Ai+1]减去1,D[Bi]加上1。其含义是:“身高减小1”的影响从Ai+1开始,持续到Bi-1,在Bi结束。最后,C就等于D的前缀和。
上述优化后的算法把对一个区间的操作转化为左、右两个端点上的操作,再通过前缀和得到原问题的解。这种思想很常用,我们在后面还会多次遇到。该算法的时间复杂度为O(N+M)。
另外,在本题的数据中,一条关系(A,B)可能会输入多次,要注意检查,对于重复的关系,只在第一次出现时执行相关操作即可。这一点需注意
#include<bits/stdc++.h>
using namespace std;
map<pair<int, int>, bool> existed;
int c[10010], d[10010];
int main() {
int n, p, h, m;
cin >> n >> p >> h >> m;
for (int i = 1; i <= m; i++) {
int a, b;
scanf("%d%d", &a, &b);
if (a > b) swap(a, b);
if (existed[make_pair(a, b)]) continue;
d[a + 1]--;
d[b]++;
existed[make_pair(a, b)] = true;
}
for (int i = 1; i <= n; i++) {
c[i] = c[i - 1] + d[i];
printf("%d\\n", h + c[i]);
}
cout << endl;
}
凡人追妹传之大学篇
可以插入到中间,左边和右边,也有可能无法插入
分别进行判断即可
我就想着不算难吧,但是就只有几个人写了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int cb[100000];
int cc[100000][2];
int main() {
int n;
while (cin >> n) {
for (int i = 0; i < n; i++) {
cin >> cb[i];
}
sort(cb, cb + n);
if (n == 1) {
cout << "-1\\n";
} else if (n == 2) {//左边 右边 中间
int c = cb[1] - cb[0];
if (c & 1) {
cout << "2\\n";
cout << cb[0] - c << " " << cb[1] + c << "\\n";
} else if (cb[0] == cb[1]) {
cout << "1\\n";
cout << cb[0] << "\\n";
} else {
cout << "3\\n";
cout << cb[0] - c << " " << cb[0] + c / 2 << " " << cb[1] + c << "\\n";
}
} else if (n >= 3) {//两个中间,左边右边,没有
//判断所有只有一个不等--中间
int pd = 0;
int min = INF;
for (int i = 1; i < n; i++) {//找最小的
if (cb[i] - cb[i - 1] < min) {
min = cb[i] - cb[i - 1];
}
}
for (int i = 1; i < n; i++) {
if ((cb[i] - cb[i - 1]) != min && (cb[i] - cb[i - 1]) == min * 2) {
//可以插入
cc[pd][0] = cb[i];
cc[pd++][1] = cb[i - 1];
} else if ((cb[i] - cb[i - 1]) != min) {
pd = -1;//直接失败
break;
}
}
//全部相同
int q = 1;
for (int i = 1; i < n; i++) {
if (cb[i] != cb[i - 1]) {
q = 0;
}
}
if (q) {
cout << "1\\n";
cout << cb[0] << "\\n";
} else {
if (pd > 1 || pd == -1) {//>=一个不等--没有
cout << "0\\n";
} else if (pd == 1) {
cout << "1\\n";
cout << (cc[0][0] + cc[0][1]) / 2 << "\\n";
} else if (pd == 0) {//所有都等,左右
int c = cb[1] - cb[0];
cout << "2\\n";
cout << cb[0] - c << " " << cb[n - 1] + c << "\\n";
}
}
}
}
}
北宋大烟篓
经典约瑟夫环问题
如果看不懂代码的可以看这里
https://blog.csdn.net/u011500062/article/details/72855826
#include <iostream>
#include <algorithm>
using namespace std;
int cir(int n, int m) {
int p = 0;
for (int i = 2; i <= n; i++) {
p = (p + m) % i;
}
return p + 1;
}
int main() {
int t;
int n, m;
cin >> t;
for (int i = 0; i < t; i++) {
cin >> n >> m;
cout << cir(n, m) << "\\n";
}
}
游戏败家子
动态规划
假设数组 cost 的长度为 n，则 n个阶梯分别对应下标 0 到 n-1，楼层顶部对应下标 n，问题等价于计算达到下标 n 的最小花费。可以通过动态规划求解。
创建长度为 n+1 的数组dp，其中dp[i] 表示达到下标 i的最小花费。
由于可以选择下标 0或 1 作为初始阶梯，因此有 dp[0]=dp[1]=0。
当 2≤i≤n 时，可以从下标 i−1 使用 cost[i−1] 的花费达到下标 i，或者从下标 i-2使用 cost[i−2] 的花费达到下标 i。为了使总花费最小，dp[i] 应取上述两项的最小值，因此状态转移方程如下：
dp[i]=min(dp[i−1]+cost[i−1],dp[i−2]+cost[i−2])
依次计算 dp 中的每一项的值，最终得到的dp[n]即为达到楼层顶部的最小花费。
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<algorithm>
int minCostClimbingStairs(int *cost, int costSize) {
int dp[costSize];
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < costSize; i++) {
dp[i] = fmin(dp[i - 1], dp[i - 2]) + cost[i];
}
return fmin(dp[costSize - 1], dp[costSize - 2]);
}
int main() {
int cost[1000];
int costSize = 0;
int n;
while (~scanf("%d", &n)) {
while (n--) {
scanf("%d", &costSize);
for (int i = 0; i < costSize; i++) {
scanf("%d", &cost[i]);
}
printf("%d", minCostClimbingStairs(cost, costSize));
}
}
}
超神排位赛
模拟题,灵感来自某年山东省省赛,有一道炉石的排位机制模拟
按照题意模拟即可,只是细节要注意,例如升段的时候,降段位的时候,王者50星,王者不会掉到星耀等几种情况
#include<bits/stdc++.h>
using namespace std;
char r[10][20] = {"", "Bronze", "Silver", "Gold", "Platinum", "Diamond", "Starry", "Master", "Challenger"};
int limit[] = {0, 3, 3, 4, 5, 5, 5, 999, 999};//星数限制
int limit2[] = {0, 3, 4, 4, 5, 5, 5, 999, 999};//分段数量限制
int rule[] = {0, 3, 3, 3, 4, 5, 6, 999, 999};//连胜规则数量
char br[6][10] = {"", "one", "two", "three", "four", "five"};
//cnt 段位下标 counter 小段位下标
int cnt, counter;
char c1[20], c2[20];
int c, n;
void ascertain() {
//cnt 段位下标 counter 小段位下标
for (int i = 0; i < 9; i++) {
if (strcmp(c1, r[i]) == 0) {//相同
cnt = i;
break;
}
}
for (int i = 0; i < 6; i++) {
if (strcmp(c2, br[i]) == 0) {
counter = i;
break;
}
}
}
void verify() {
//王者判定
if (c > limit[cnt] && cnt != 7) {
c -= limit[cnt];
counter--;
if (counter == 0) {
cnt++;
counter = limit2[cnt];
}
}
}
int main() {
int cb[1000];
while (cin >> c1 >> c2 >> c) {
ascertain();//使cnt,counter,c转化为数字
cin >> n;
int plus = 0;
for (int i = 0; i < n; i++) {
cin >> cb[i];
//判断连胜的过程
//判断加星升段的过程
if (cb[i] == 1) {//连胜场数
plus++;
} else {
plus = 0;
}
if (plus == rule[cnt] && cb[i] == 1) {//可以连胜
c += 2;
verify();
plus = 0;
} else if (cb[i] == 1) {//普通胜利
c++;
verify();以上是关于2021-BNUZ-IT节程序设计竞赛网络赛题解的主要内容，如果未能解决你的问题，请参考以下文章
“今日头条杯”首届湖北省大学程序设计竞赛（网络同步赛 ）--B. Salty Fish Go!
H. GSS and Simple Math Problem--“今日头条杯”首届湖北省大学程序设计竞赛（网络同步赛）