GMS：基于网格运动统计的快速极度鲁棒的特征匹配

Posted 2021-05-08 猛龙过江ing

滚滚长江东逝水，浪花淘尽英雄。是非成败转头空。——（明）杨慎《临江仙》

有段时间没有写博客了，最近技术上没有什么分享的，就翻译一篇CVPR论文吧！博主之前一直是看IEEE和MDPI的论文多一些，可能也比较适应了，再一看CVPR，感觉语言风格相差挺大的。这篇文章比较经典，以后也会经常用到，所以与其每次看都特别费劲，还不如直接翻译成中文，一劳永逸地解决这个问题。闲言少叙，精彩马上就来——

摘要

众所周知，将平滑度约束集成到特征点匹配中可以使特征匹配变得非常鲁棒。然而，这种方案既复杂又运行缓慢，这使得它在视频应用中无法使用。本文提出了基于网格的运动统计方法，即GMS（Grid-based Motion Statistics），该方法将一个区域中一定数量匹配的统计似然性视为运动平滑度。GMS可以将特征点匹配的数量之多转化为质量之精。它提供了一个可以实时运行的、极度鲁棒的匹配方法。通过在视频中、弱纹理环境下、模糊图片上以及宽基线数据里进行验证，GMS始终优于其他的可以实时运行的特征匹配算法，并且可以取得同更复杂、运行更缓慢的算法相当的精度。

1 简介

在许多计算机视觉的算法中，特征点匹配都是基本输入数据。因此，它的速度、精度和鲁棒性就变得尤其重要。现阶段，慢（但是鲁棒）的特征匹配算法和快（但是不稳定）的特征匹配算法间的性能差距非常大。

关键问题在于应用于更强大的特征匹配算法中的一致性约束（邻近的像素运动相似）。一致性是一个强大的约束，但是稀疏特征点缺少明确定义的邻域。这使得基于一致性的特征匹配不但计算量大而且复杂难以实现。本文提出了GMS方法，它把统计学上邻域对之间具有一定数量的特征匹配的可能性作为平滑度约束。我们发现GMS可以快速、可靠地区分正确和错误的特征匹配，可以得到高质量的特征匹配，如图1所示。

 本文受到了双边函数（Bilateral Function,BF）的启发。双边函数指出：特征匹配缺少的原因不是特征匹配太少，而是很难区分正确匹配和错误匹配。双边函数说明了用复杂极小化计算的相干测度来实现这种分离的可行性。双边函数算法非常奏效（尽管有点慢）。然而，它主要是由观察和直觉推动的。由于缺乏清晰的理论，所以提升非常困难，因此研究人员必须依赖于对图像数据的经验测试，但是经验测试是受许多波动变量影响的。

我们发现双边函数和其他算法使用的复杂的平滑度约束可以缩减成一个简单的描述：运动平滑使得匹配聚类不太可能随机出现。因此，分离正确匹配和错误匹配的策略可以简化为计算该特征匹配邻域内特征匹配的数量。根据大数定律，邻域内特征匹配的数量越多，匹配为真值的可能性也就越大。数学分析是十分直接的，但结果可能会改变范式。

之前的特征匹配的论文假设匹配的质量主要随着特征不变性和独特性的改进而提高。GMS给出了一个新的提高特征匹配质量的方向：原始特征匹配的数量也会影响质量。由于检测更多的特征点比设计新的描述子简单，GMS有望为以前难以解决的特征匹配问题提供简单的方案，就像图1所示。

综上所述，本文的贡献如下：

1、将运动平滑度约束转化为统计测量数据来剔除错误的特征匹配。我们发现这个约束方法可以应对之前棘手的场景。

2、开发了一个有效的基于网格的分数估计器，它可以集成到特征匹配算法中，并实现实时运行。

3、在标准比率测试中，证明了本文提出的GMS算法明显好于传统的SIFT算法、SURF算法以及最近提出的使用CNN训练的LIFT算法。

1.1 相关工作

特征点匹配的基础工作是寻求提升特征描述子的独特性和不变形并提升特征点的位置精度，这其中包括了一些经典的工作，例如SIFT、ORB、SURF、A-SIFT、Harris角点以及一些仿射协变区域检测算法。这其中的许多算法是需要GPU加速才能实现实时运行或者近似实时运行的。除此之外，有一些使用FLANN的算法来对特征匹配进行加速，这些研究仍在进行当中，最近的一个例子就是使用CNN训练的LIFT描述子。总之，以上的工作共同构成了本文算法的核心基础。

关键困难是在单纯依赖描述子的情况下很难区分正确匹配和错误匹配，这导致了需要剔除大部分正确的匹配来减弱错误匹配的影响。RANSAC算法算法可以利用几何信息来缓解这个问题。然而，RANSAC算法要求大部分的错误匹配要被预先剔除，并且无法处理所有最近邻匹配集中存在大量的错误匹配的情况。

最近，一些算法使用匹配分布约束来分离正确匹配和错误匹配。然而，这些算法使用了复杂的平滑度约束，这种约束不但难以理解而且计算量大。本文的方法受到这些方法的启发，使用了更加简单更容易理解的统计匹配约束，这使得匹配具有高精度和强鲁棒性。

更通俗地说，本文的方法和光流相关，使用了可以直接使用平滑度来帮助剔除匹配的基于点的相关性算法和批量匹配算法。这些算法非常有效，同时它们也非常复杂、计算量巨大。最后，我们指出我们从其他优秀的研究人员那里获得了一些灵感，例如可以将许多个弱学习算法整合成一个强学习算法的AdaBoost。我们给出GMS的设计理念：使用平滑度约束来综合来自多个匹配的信息，以使算法做出高质量的决策。

2 本文的方法

给定对于同一个三维场景的从不同视角拍摄的一组照片，一组特征点匹配指的是在一幅图像中的一个像素（特征点）和它在另一幅图像中的对应的点。如果运动是平滑的，邻域像素和特征点会是一起运动的，这使得我们可以做出如下假设：

假设1：平滑的运动使正确匹配周围的（小）邻域具有相同的3D位置。同理，错误匹配周围的邻域在几何上的3D位置是不同的。

这里的邻域定义为一组对应特征点在两幅图像中的周围区域，正如图2所示。

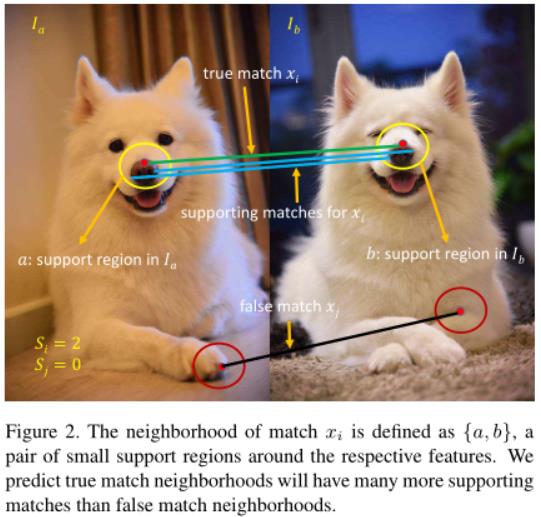
 假设1意味着正确匹配的邻域，在3D场景下对应相同的位置区域，因此在两个图像共享许多相似的特征。这就导致了在邻域中有许多的匹配支持。反之，错误的特征匹配对应不同的3D场景，有非常少的相似的特征匹配，这减少了匹配的支持。我们把这一机制封装到一个叫做GMS的统计框架中，来可靠地分离正确的特征匹配和错误匹配。第三部分介绍了快速邻域分数计算的网格算法，第四部分介绍了实验结果和与其他算法的比较结果。

2.1 符号

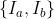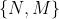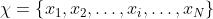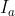一组对应的图像分别有个特征点。是从图像到图像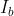的所有特征点匹配的邻域集合。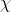有基数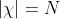。我们的目标是通过局部支持的特征匹配把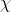分成正确匹配和错误匹配两个集合。

图片2中的特征匹配邻域符号含义如下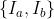：对应的区域分别表示为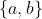，它们额外（除去原始的特征匹配）分别有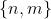个特征点匹配。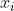是匹配的对应区域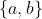的匹配的子集。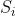是表示邻域支持度的数值：（公式1），其中-1代表从总和中去除原始的特征匹配。

2.2 基本统计约束

由于邻域很小，我们只考虑理想化的正确区域对和错误区域对，忽略部分位置相似的情况。令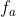为在区域a中有n个特征支持的特征匹配。设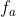为正确匹配的概率为t，我们的目标是分离出在3D位置相同和不同的情况下，对应的特征匹配点到达该邻域的概率。表1总结了常用的标记和事件，图3说明了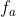的事件空间。

 为了让问题易于处理，我们做出如下假设：

假设2：设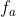为错误匹配，则它的最近邻域中的匹配可能位于M个位置中的任何一个。

假设2之所以发生是因为通常情况下，没有先验的理由使一个错误的特征匹配的最近邻域偏向图像的任何区域。假设2给出（公式2），（博主注：在匹配错误的情况下进入某网格的概率）

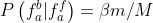
其中m是在区域b中的特征匹配的数量，β是为适应违反假设2而增加的因子，例如像一排窗户一样重复的结构会造成假设的不成立。

令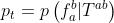为给定的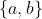 在3D场景中为相邻位置的概率，特征点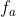的最近邻域在区域b中。因此（公式3），（博主注：此处为匹配进入相同小网格的概率）

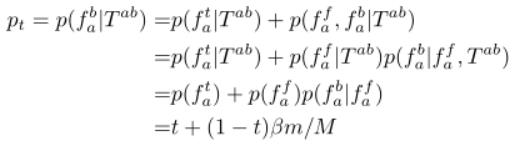
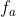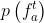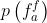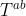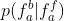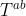 解释：图3（i）表示事件只在匹配正确或者匹配错误但是欧坦位于区域b中时才发生，这就得到了上述公式的第一行。第二行由贝叶斯法则得出。由于特征点预先匹配，和独立于。由于假设2，同样独立于。排除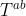，从表1中的值进行替代，公式2给出了最后的表达。

令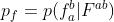。对公式3进行简化（公式4），（博主注：此处为匹配进入不同小网格的概率）

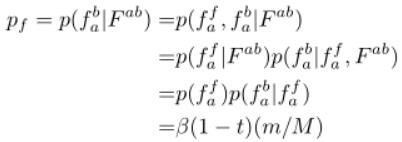
解释：从图3（ii）中我们知道事件 是事件的子事件。因此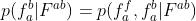，，这也就是公式4的第一行。与公式3相似，根据贝叶斯法则可以将概率扩展为独立于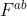的子概率。替代值来自于表1，公式2给出了最终的表达。

由于每一个特征匹配都是独立的，使用假设1和公式（3）（4），我们可以粗略估计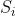的分布，它是特征匹配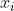在邻域内特征匹配的数量，服从一对二项分布（公式5）：

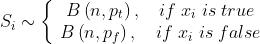
公式5似乎有点复杂，重要的点是正确和错误的匹配的邻域分数S服从的分布很不一样。这就意味着S的整体概率分布函数是一个潜在的二项分布，这使得分数S是一个区分正确特征匹配和错误特征匹配的有效的指标。如图4所示。

2.3 一般化多邻域

在一个大的区域范围中运动通常是平滑的。然而，假设1要求充足的小邻域。如果邻域过大，正确的特征匹配邻域会包括一些错误的匹配区域，反之亦然。这降低了正确和错误分数分布的可分离性。因此，概括假设1，我们有：

假设3：如果在一个区域中运动是平滑的，那么正确的匹配在多个邻域对上都具有相同的3维空间位置，而错误的匹配在多个邻域对上的3维空间位置则相对不同。

这里给出一个更加一般化的分数（公式6）：

其中K是预测随着特征匹配i一起移动的小邻域的数量。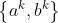是预测的区域对，是位于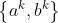的特征匹配的子集。

假设每个区域对有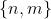个特征点，类似于公式5，假设3表明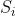服从二项分布（公式7）：

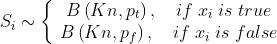
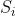 分布的均值和标准差分别为（公式8）：

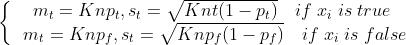
通常，当处理统计事件时，我们认为一个偏离平均值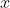个标准差的事件是极不可能发生的。这正如图4中展示的那样，并且它可以用可分性分数来量化（公式9）：

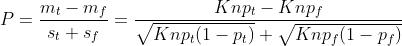
我们的目标是设计算法获得P的最大值。

2.4 分析

这些派生很简单。然而，它们使得我们的直觉更加有条理能够得出一些有用的结果。

数量-质量平衡：这些派生的关键结果是（公式10）：

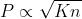
这意味着，假设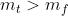，正确匹配和错误匹配的可分性随着特征匹配的数量n的增大而无限增大。即使对于正确匹配很少的困难的场景，如果正确匹配的位置比随机位置有更多的匹配，只要特征匹配的数量足够的大，我们就可以以完美的精度和召回率获得尽可能多的特征匹配。这种形式将假设1、2、3与大数定律直接联系起来。这个推论的结果是很好的，因为以前大多数的工作假设更好的特征匹配的关键是增加特征点的独特性和不变性。相反，公式（10）表明原始特征匹配的数量的增大有助于特征匹配质量的提高。这使得通过增加特征匹配数量来解决有挑战性的特征匹配问题成为可能，图5给出了一个例子。

 运动预测：通常情况下，简单地增大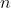是不切实际的。公式（10）给出了一个替代方法：通过预测图像区域的更多联合运动来增加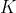。我们使用这个方法来实现可以实时运行的特征匹配剔除算法。

实际适用性：通过使特征匹配的数量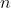足够大，GMS约束会非常强大。问题时在实际应用中如何判断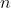是否已经足够大。给定10000个均匀分布的特征点，一些经验数值如下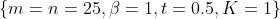：。因此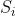，的在公式（8）的基本约束中的平均值和标准差为（公式11）：

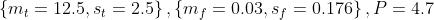
这存在明显的区别。注意。这表明GMS约束在正常的特征匹配数量上非常强大。这也在某种程度上解释了一些算法采用简单的策略取得了很好的效果。

与描述子的关系：可分性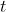与正确匹配的百分比的关系由一下公式给出（公式12）：

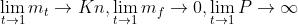
随着最近邻匹配的趋于完美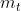，逐渐趋向于它的最大值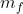，逐渐趋向于它的最小值，可分性逐渐趋向于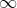。因此，如果设定一个固定的阈值，通过使用一个较大的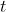值，GMS能够在简单的场景中取得更好的结果。这在实际应用中十分重要，因为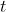是未知的，并且依赖于使用的场景。通过允许它随着特征描述子设计的改进而变化，GMS的普遍适用性得到了进一步的提高。

3 应用于快速记分的网格框架

本节将之前的分析转化为一种有效的实时匹配算法。3.1部分介绍了网格框架，它解决了一些问题，例如：a）通过网格单元进行有效的分数计算；b）将哪些邻域（网格单元）组合在一起；c）使用多少个网格单元；d）如何有效地计算阈值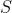。算法1给出了实施概述，具体细节在3.2部分进行讨论。

3.1 网格问题

a）有效地分数评估。对每个特征匹配的邻域进行评分的时间复杂度是O(N)，N为图像特征匹配的数量。这与我们希望使用尽可能多的特征点相矛盾。我们通过将图像分成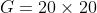个大小相似的不重叠的网格来解决这个问题。潜在的网格匹配的分数只需要计算一次。所有被认为是正确的网格匹配中的特征匹配都会被接受。这使得计算复杂度与特征匹配数量无关，达到了O(1)。在实际应用中，许多特征点位于网格的边缘。为了适应这一点，我们在X和Y两个方向上移动半个单元格宽度和高度，重复该算法3次以上。

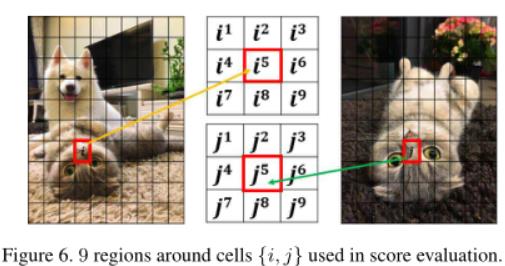
b）分组匹配邻域（单元对）以增强鲁棒性。正如公式（6）和公式（7）说明的，通过对单元对分组增加了可分割性。我们使用平滑横向运动假设对单元格对进行分组。因此根据公式（6），对于单元格对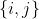的分数为（公式13）：

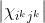其中，为网格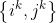中的特征匹配的数量，如图6所示。这种解决方案是有效的，但是限制了平面内的旋转不变性。GMS在极速旋转下的比率测试中比较有竞争力，如图8所示，但是旋转越小性能越好。在实践中，旋转通常可以通过其他传感器来估计，在实际应用中OpenCV 3.0使用EXIF信息将所有读取到的图像自动旋转到规范的方向。另外，我们还提供了一个缩放和旋转版本的算法，算法在所有现在的缩放-旋转网格对上执行网格选择并从具有最佳结果的网格对中选择最佳匹配。

c）应该使用多少个小网格？更多的网格可以提升匹配的质量。然而，这样会使得每个单元格中的特征匹配的数量变小，导致可分割性变小。这个可以通过增大来补偿，但是这样会增大计算量。我们的理论和经验结果表明网格数量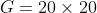，取10000个特征点。此时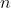的平均值为25。特征点数量更多时可以使用更多的网格。

d）通过阈值将网格对分为正确和错误两个集合。

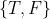图4展示了期望的阈值可以设定为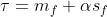，其中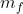是平均值而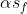是可以确保大多数错误的网格单元匹配被拒绝的适当倍数的标准差。实际上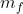，的设计值很小，而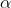很大以确保拒绝大量错误的网格对。使用符号来进行标记说明，阈值可以近似为。

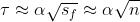这样可以得出单参数阈值函数（公式14）：

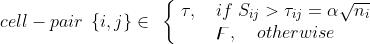
其中，是根据实验确定的，是单个网格中特征点的平均数量（例如，图6中是9个网格）。

3.2 实施细节

我们使用OpenCV的ORB特征点。特征点的数量固定为10000，它是可以实现实时运行的最大数量。对于较大的、纹理丰富的图片可以设置多于10000个特征点。这样会导致特征点分布不均匀（聚集在角落）。对于较小的、纹理较少的图片可以设置少于10000个特征点。前一个问题将所有图像调整为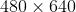大小来解决。后一个问题通过设定FAST特征点的阈值为0来解决。这样就可以在弱纹理环境中实现特征匹配（参见随附视频）。最近邻域是通过在GPU上根据汉明距离暴力匹配来实现的，这与使用CPU进行的特征点检测并行运行。这是两个计算量最大的模块。最终，正确的特征匹配通过GMS算法筛选出来，这一步骤在单线程CPU上耗费1ms。给出代码的链接：https://github.com/JiawangBian/GMS-Feature-Matcher。

4 实验

GMS是一个对传统的使用比率测试来剔除错误匹配的高效、有效的替代方案。我们通过两个指标来评价GMS：a）它的召回率、精确度以及F值，F=2·(Precision·Recall)/(Precision+Recall)，以此来代替比率检验；b）GMS的特征匹配在提升SLAM和SfM位姿估计上的有效性。我们将GMS同快速匹配算法如SIFT、SURF、ORB、USAC以及强大但是运行较慢的匹配算法如BF、BD、DM、GAIM、LIFT进行比较。

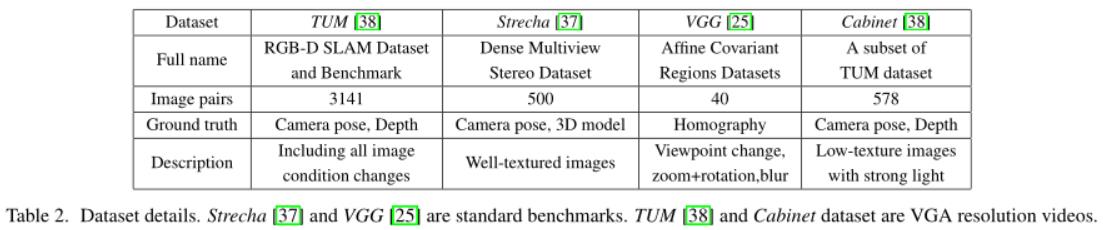
4.1 数据集

我们在四个数据集中进行测试：TUM、Strecha、VGG以及Cabinet，具体介绍见表2。TUM数据集有六个宽基线、弱纹理、模糊的具有挑战性的视频序列。场景如图7所示。Strecha（为适应较慢的算法，图片采用四分之一大小）和VGG是带有大量宽基线和良好的真值的标准数据集。Cabinet数据集（图7上方中间）是TUM的子集，允许对弱纹理场景进行单独分析。

 每一个TUM视频被分成100帧为一组。第一帧的坐标系被指定为参考系。如果一个集合中的所有帧的相对旋转小于30°，它们将与参考系匹配。对于Strecha数据集也采用相似的处理，只是每一个图片都是一个参考系。

4.2 结果

我们将GMS的结果与其他匹配算法进行对比分析。

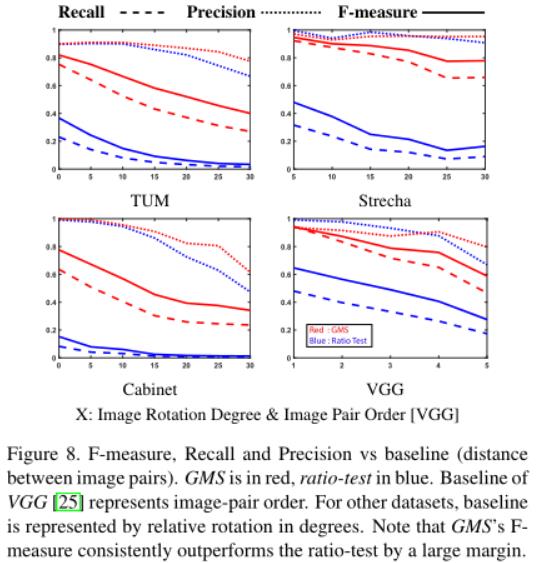
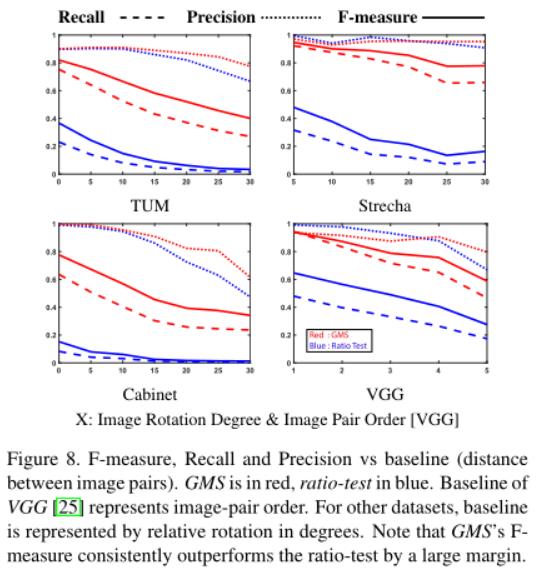
精确度&召回率：我们将GMS同传统的比率测试（阈值0.66）进行比较。精度、召回率和F值如图8所示。GMS是红色的线，比率测试是蓝色的线。每一个指标都用唯一的线条样式表示。GMS的F值始终大幅高于比率测试。这在VGG数据集上表现得尤为明显，该数据集中有明显的平面内旋转。回想3.1部分，我们的方案牺牲了旋转的性能。

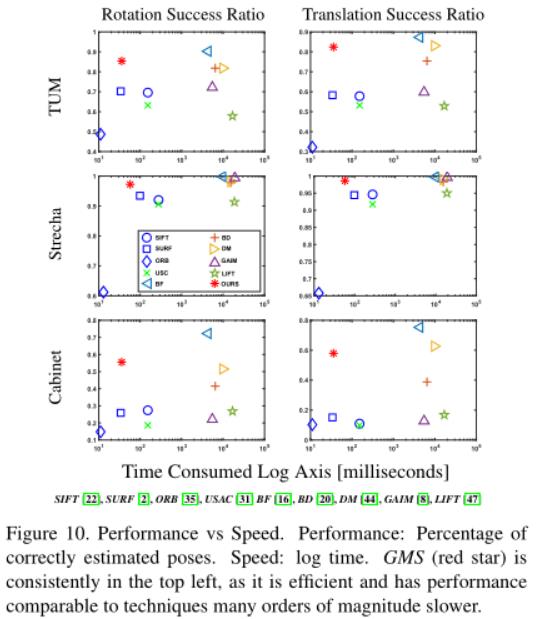
精度&速度：匹配的速度可以说和性能一样重要。图10给出性能和素服权衡的结果。性能是通过精确估计的姿态百分比来量化的，而速度是以毫秒为单位的时间记录来衡量的。如果其旋转和平移误差分别在5%和15%之内，则位置姿态估计被认为是正确的。图10展示了GMS（红色）保持了高速度和高性能。GMS的性能比其他快速算法高得多并且与慢多个数量级的算法（例如：BF和Deep-Matching）相比性能相当。根据我们的经验，几乎所有纯粹基于特征点的算法都可以通过使用GPU来实现实时运行。算法在中央处理器上1毫秒的计算成本，GMS保持了它们的实时运行的特性。使用GMS进行完全匹配可以达到每秒27.8帧的速度。

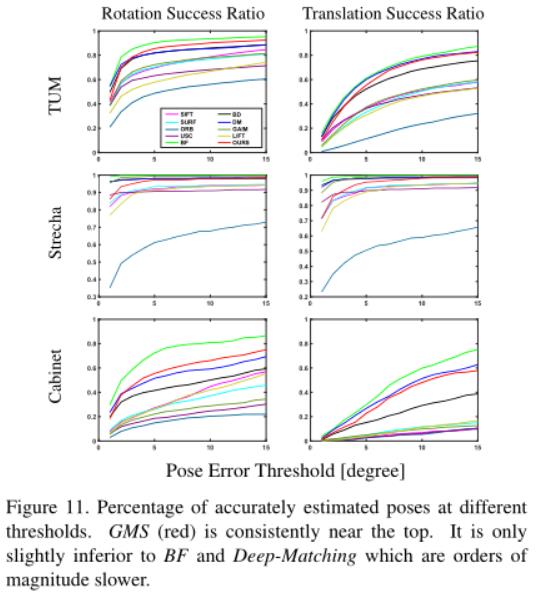
 完整的性能曲线：为了确保图10的阈值选择的公平性，图11绘制出了不同阈值的性能曲线。观察发现GMS的相对性能没有发生改变。

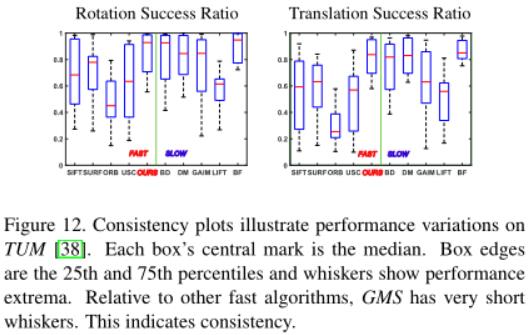
一致性：先前的实验侧重于平均结果。图12展示了在不同TUM数据集场景中的性能变化。每一个盒子的中心标记是中位数。盒子的边缘表示下四分位数和上四分位数。形似须状的表示了性能的非正常值。根据下方的形似须状的线表明大多数快速算法一致性差。GMS（红色）在快速算法中的一致性最好；与慢很多的算法相比，一致性相当。

 视频结果：GMS能够处理视频数据中宽基线的特征匹配。图9提供了视频的截图作为补充。

 5 结论

我们提出了一种基于邻域匹配数量来分离正确匹配和错误匹配的统计方法——GMS。虽然其他算法已经隐含地采用了这种约束，但是我们的算法理论性更强、更简单、更快速而性能也没有下降。除此之外，GMS揭示了特征匹配数量和匹配质量之间的一个联系。这可能是一个有趣的研究方向，能够处理以前难以解决的匹配问题。

终于翻译完了，我真的是不太适应这篇文章的语言风格，看得我头晕脑胀的。好在是弄完了，接下来就可以直接看中文版的好好学习研究了。毕竟是开源的，所以还是比较容易移植的，可以用到自己的研究当中，O(∩_∩)O哈哈~