Dijkstra算法介绍及其优先队列优化和斐波那契堆优化
Posted 2020.7.30
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Dijkstra算法介绍及其优先队列优化和斐波那契堆优化相关的知识,希望对你有一定的参考价值。
Dijkstra算法介绍及其优先队列优化和斐波那契堆优化
文章目录
一、dijkstra算法概述
- Dijkstra算法解决的是带权重的有向图上单源最短路径问题,使用此算法的前提条件是所有边的权重都为非负值。
- 算法重复从节点集中选择最短路径估计估计最小的节点u,然后对所有从u发出的边进行松弛(更新节点u的所有子节点到节点u的距离)。
二、实现dijkstra算法需要掌握的算法知识
1、从数据中剔除最小项(函数ExtractMin())
-
如果只是处于练习的目的,可以通过遍历所有节点(通常可以将所有节点存储于链表中,链表关键字为与父节点间的距离,主要卫星数据是本节点名称,及本节点的所有子节点的名称和二者间的距离)找到与源节点相距最短的节点(源节点的距离初始化为0,其他节点距离初始化为max),删除并返回该节点。但是这样做及其耗费时间。
-
使用优先队列(二叉堆实现,在后面讲解)删除并返回一个节点,优先队列指的是某个节点的值至多与其父节点一样大。因此,堆中的最小元素存放在根节点中(A[1])。因此,我们只需将根节点作为返回值,并删除根节点即可。
-
使用斐波那契堆删除并返回一个节点,斐波那契堆含有一个指向具有最小关键字的指针,因此只需删除并返回该指针即可。
2、松弛操作
伪代码:
Relax(u,v,w)//u为节点v的父节点
{
if v.d>u.d+w(u,v)//w(u,v)表示从节点u到节点v的距离
v.d=u.d+w(u,v)//更新子节点距离
v.Π=u//将节点u最为节点v的新的父节点,属性Π表示v的父节点,本人代码使用f_dis、f_time、或father表示
}
松弛操作对应优先队列和斐波那契堆中的关键字减值。
3、伪代码分析
实现Dijkstra的伪代码:
Dij(G,w,s)//G表示所有节点的集合,s表示源节点
Q=G.V//使用一个最小优先队列保存节点(基于二叉堆的优先队列或者斐波那契堆)
while Q!=NIL //只有图中还有节点
u=ExtractMin(Q)
for each vertex v∈G.Adj[u]//对于节点u的每一个子节点
Relax(u,v,w)//w表示一个属性,即节点u与节点v间的距离
可见,算法本身很简单,但其涉及的函数是比较难以用高效的方法实现的。
三、最小优先队列概述
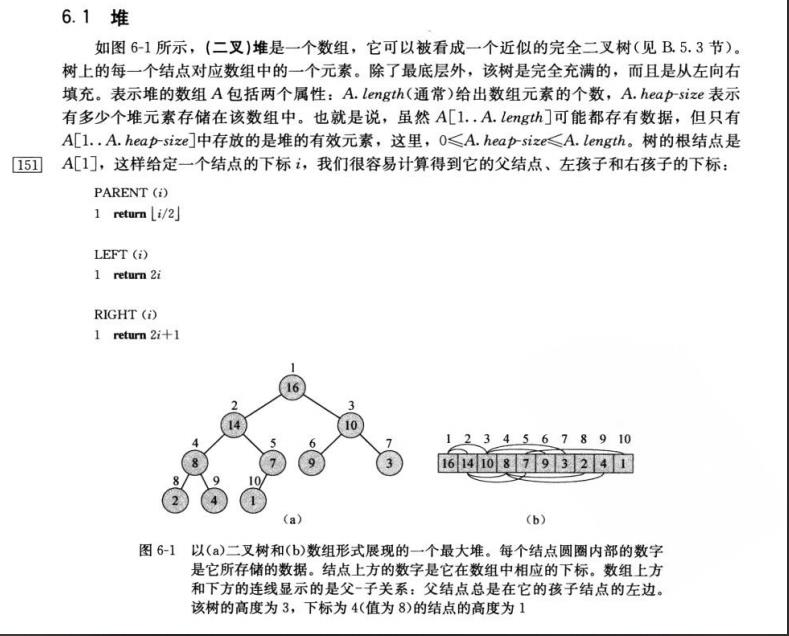


四、最小优先队列伪代码分析
1.维护堆的性质
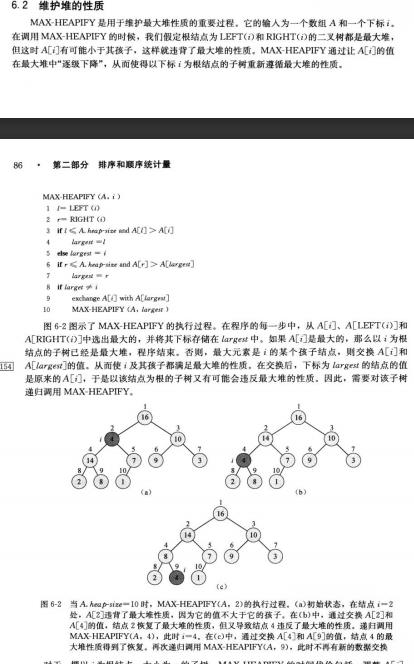
图片中展示的是建立最大堆,建立最小堆需要改为:A[l]<A[i],以此类推。
2.建堆

所谓叶节点:就是下图中的节点8、7、6、9及其上面的节点。
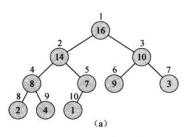
3.剔除最小节点
ExtractMin(A)
if A.heap-size<1//已经是空堆
error "heap underflow"
min=A[1]
A[1]=A[A.heap-size]//这种直接赋值在实现中不可取,应该交换二者的值(地址)
A.heap-size=A.heap-size-1//实现了删除一个节点
MaxHeapIfy(A,1)
return min
4.关键字减值(松弛操作,具体实现中将此函数命名为relax())
图片中描述的是最大堆的性质,类比即可。

HeapReduceKey(A,i,key)
if key>A[i]
error "new key is big than curren key"
while i>and A[parent[i]]<A[i]
exchange A[i] with A[parent[i]]
i=parent[i];
五、例题分析
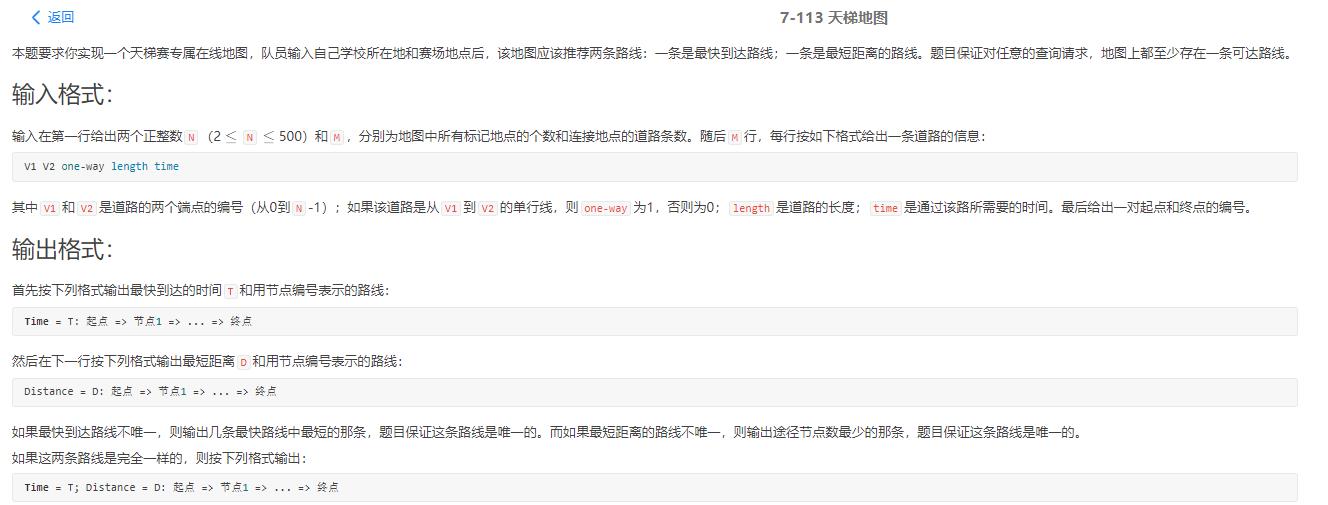
输入样例:
10 15
0 1 0 1 1
8 0 0 1 1
4 8 1 1 1
5 4 0 2 3
5 9 1 1 4
0 6 0 1 1
7 3 1 1 2
8 3 1 1 2
2 5 0 2 2
2 1 1 1 1
1 5 0 1 3
1 4 0 1 1
9 7 1 1 3
3 1 0 2 5
6 3 1 2 1
5 3
输出样例:
Time = 6: 5 => 4 => 8 => 3
Distance = 3: 5 => 1 => 3
1. 首先设法存储输入的数据
我们将所有节点数和道路条数分别记为all_pos、all_way,将起点和终点分别记为start、end。将道路信息存储至结构中。
typedef struct min{
int pos;//本节点名称
int son[3][1000];//子节点名称及属性,son[0][i]表示子节点名称,
//对应的son[1][i]表示pos节点到son[0][i]节点的距离,son[2][i]表示对应时间
int k;//子节点数目(松弛操作需要)
int about_dis;//距离源节点可能的最小距离
int about_time;
int point;//根据题目表述建立的一个变量,表示节点个数
struct min *f_time;
struct min *f_dis;//父节点
}Min;
2. 设计最小优先队列
typedef struct heap{
Min *A[1000];//用于存储节点
int sta[1000];//用于存储每一个关键字(节点名称)在数组A中的位置
//如H->sta[key]表示关键字key在数组A中的位置,他是优化过程的核心。
int heap_size;//数组A中符合优先队列的元素个数
int length;//数组A的长度(为节约空间,应与all_pos一致)
}Heap;
3.实现Dijkstra算法(限于题目要求,略显臃肿)
/*dij*/
void dij(Heap *H,int opt)
{
/*求距离*/
if(opt==1)
{
while(!IsEmpty(H))
{
Min *u=ExtractMin(H,opt);
for(int i=0;i<u->k;i++)
relax(H,u,i,opt);
}
}
/*求时间*/
else
{
while(!IsEmpty(H))
{
Min *u=ExtractMin(H,opt);
for(int i=0;i<u->k;i++)
relax(H,u,i,opt);
}
}
}
Min *ExtractMin(Heap *H,int opt)
{
if(opt==1)
{
Min *u=H->A[1];
H->sta[H->A [1]->pos]=H->heap_size ;//更新关键字在数组A中的位置,关键操作。
H->sta [H->A [H->heap_size ]->pos]=1;
H->A [1]=H->A[H->heap_size ];
H->A [H->heap_size ]=u;
H->heap_size--;
MaxHeapIfy(H,1,opt);
return u;
}
else
{
Min *u=H->A[1];
H->sta[H->A [1]->pos]=H->heap_size ;
H->sta [H->A [H->heap_size ]->pos]=1;
H->A [1]=H->A[H->heap_size ];
H->A [H->heap_size ]=u;
H->heap_size--;
MaxHeapIfy(H,1,opt);
return u;
}
}
void relax(Heap *H,Min *u,int p,int opt)
{
Min *s=H->A[H->sta[u->son[0][p]]];
int i=H->sta[u->son[0][p]];
if(opt==1)
{
if(s->about_dis>(u->about_dis +u->son[1][p]))
{
s->f_dis =u;
s->about_dis=u->about_dis +u->son[1][p];
s->point=u->point+1;
while((i>1)&&(H->A[i/2]->about_dis >H->A[i]->about_dis))
{
H->sta[H->A[i/2]->pos]=i;
H->sta[H->A[i]->pos]=i/2;
Min *temp=H->A[i/2];
H->A[i/2]=H->A[i];
H->A[i]=temp;
i=i/2;
}
}
else if((s->about_dis==(u->about_dis +u->son[1][p]))&&(s->point>=u->point+1))
{
s->f_dis =u;
s->point=u->point+1;
s->about_dis=u->about_dis +u->son[1][p];
while((i>1)&&(H->A[i/2]->about_dis >H->A[i]->about_dis))
{
H->sta[H->A[i/2]->pos]=i;
H->sta[H->A[i]->pos]=i/2;
Min *temp=H->A[i/2];
H->A[i/2]=H->A[i];
H->A[i]=temp;
i=i/2;
}
}
}
/*求时间*/
else
{
if(s->about_time>(u->about_time+u->son[2][p]))
{
s->f_time=u;
s->about_time=u->about_time+u->son[2][p];
while((i>1)&&(H->A[i/2]->about_time>H->A[i]->about_time))
{
H->sta[H->A[i/2]->pos]=i;
H->sta[H->A[i]->pos]=i/2;
Min *temp=H->A[i/2];
H->A[i/2]=H->A[i];
H->A[i]=temp;
i=i/2;
}
}
else if((s->about_time==(u->about_time+u->son[2][p]))&&(s->about_dis>=(u->about_dis+u->son[1][p])))
{
s->f_time =u;
s->about_time=u->about_time+u->son[2][p];
while((i>1)&&(H->A[i/2]->about_time>H->A[i]->about_time))
{
H->sta[H->A[i/2]->pos]=i;
H->sta[H->A[i]->pos]=i/2;
Min *temp=H->A[i/2];
H->A[i/2]=H->A[i];
H->A[i]=temp;
i=i/2;
}
}
}
}
bool IsEmpty(Heap *H)
{
if(H->heap_size ==0)
return true;
return false;
}
4.与优先队列有关的函数
/*与优先队列有关的函数*/
void BuildMinHeap(Heap *H,int opt)
{
/*求距离*/
if(opt==1)
{
H->heap_size=H->length;
for(int i=H->length/2;i>=1;i--)
MaxHeapIfy(H,i,opt);
}
/*求时间*/
else
{
H->heap_size=H->length;
for(int i=H->length/2;i>=1;i--)
MaxHeapIfy(H,i,opt);
}
}
void MaxHeapIfy(Heap *H,int i,int opt)
{
/*求距离*/
if(opt==1)
{
int l=2*i,r=2*i+1,min;
if((l<=H->heap_size)&&(H->A[l]->about_dis<H->A[i]->about_dis))
min=l;
else
min=i;
if((r<=H->heap_size )&&(H->A [r]->about_dis<H->A[min]->about_dis))
min=r;
if(min!=i)
{
H->sta[H->A[min]->pos]=i;
H->sta[H->A[i]->pos]=min;
Min *temp=H->A[i];
H->A[i]=H->A[min];
H->A[min]=temp;
MaxHeapIfy(H,min,opt);
}
}
/*求时间*/
else
{
int l=2*i,r=2*i+1,min;
if((l<=H->heap_size)&&(H->A[l]->about_time<H->A[i]->about_time))
min=l;
else
min=i;
if((r<=H->heap_size )&&(H->A [r]->about_time<H->A[min]->about_time))
min=r;
if(min!=i)
{
H->sta[H->A[min]->pos]=i;
H->sta[H->A[i]->pos]=min;
Min *temp=H->A[i];
H->A[i]=H->A[min];
H->A[min]=temp;
MaxHeapIfy(H,min,opt);
}
}
}
void InitializeHeap(Heap **H,int all_pos)
{
if(*H==NULL)
*H=(Heap 以上是关于Dijkstra算法介绍及其优先队列优化和斐波那契堆优化的主要内容,如果未能解决你的问题,请参考以下文章