第十二届蓝桥杯C++赛后感
Posted Jozky86
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第十二届蓝桥杯C++赛后感相关的知识,希望对你有一定的参考价值。
注:有些代码忘了考试时怎么写的了,(我也懒得重新写),所以很多题的代码是acwing蓝桥杯讲解里的,我对其进行注释和修改
A 空间

32位程序中,INT变量占用4个字节
1mb=1024kb
1kb=1024B
1B=8b
B:byte
b:bit
32位二进制数是四个字节
实际上就是求256MB有多少个32 bit
答案:256*1024*1024/4
= 67108864
卡片

直接模拟即可
#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\\n",a,b)
typedef long long ll;
using namespace std;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);
return s*w;
}
int a[10];
bool iff(int x)
{
while (x)
{
int y = x % 10;
if (a[y])
a[y]--;
else
return 0;
x /= 10;
}
return 1;
}
int main() {
for (int i = 0; i <= 9; i++) a[i] = 2021;
for (int i = 1;; i++)
{
if (!iff(i))
{
cout << i - 1 << endl;
break;
}
}
return 0;
}
答案:3181
直线

比赛时用set实现的,忘了自己做的对不对。。
我当时做的方法是因为两点确定一线,所以枚举两个点,然后用set记录斜率和截距(y=k*x+b),但是k有可能不存在,所以最后的答案还要额外加上20
当时代码懒得写了,按照其他博主的写法重新写的,只不过用的不是set,存下所有k和b后,排序,将重复的k和b删掉
#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\\n",a,b)
typedef long long ll;
using namespace std;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);
return s*w;
}
const int maxn = 200000;
double eps=1e-8;
int n;
struct Line
{
double k, b;
bool operator< (const Line& t) const
{
if (k != t.k) return k < t.k;
return b < t.b;
}
}L[maxn];
int main()
{
for (int x1 = 0; x1 < 20; x1 ++ )
for (int y1 = 0; y1 < 21; y1 ++ )
for (int x2 = 0; x2 < 20; x2 ++ )
for (int y2 = 0; y2 < 21; y2 ++ )
if (x1 != x2)
{
double k = (double)(y2 - y1) / (x2 - x1);
double b = y1 - k * x1;
L[n ++ ] = {k, b};//存两点所形成的直线
}
sort(L, L +maxn);
int res = 1;
for (int i = 1; i < n; i ++ )
if (fabs(L[i].k - L[i - 1].k) > eps || fabs(L[i].b - L[i - 1].b) > eps)//说明不是一条直线
res ++ ;
cout << res + 20 << endl;//加20是因为k不存在的直线也要考虑
return 0;
}
我当时的做法是对的,但是最后的答案忘了是不是这个
答案:40257
货物摆放

LWH都是n的约数,问有多少种方案,其实就是求n的约数,用这些约数进行组合。因为约数不是很多,所以三重循环枚举约数,看是否等于n
对n求约束,直接开方求就行(因为如果x是约数,那么n/x也是,所以只需要将范围缩小到根号n)
(比赛时我是这么做的,确信)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
int main()
{
LL n;
cin >> n;
vector<LL> d;
for (LL i = 1; i * i <= n; i ++ )
if (n % i == 0)
{
d.push_back(i);
if (n / i != i) d.push_back(n / i);
}
int res = 0;
for (auto a: d)
for (auto b: d)
for (auto c: d)
if (a * b * c == n)
res ++ ;
cout << res << endl;
return 0;
}
答案:2430
路径

就是一个建边跑最短路。。比赛时忘了gcd咋写emm
好像有的用dp来做?
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2200, M = N * 50;
int n;
int h[N], e[M], w[M], ne[M], idx;
int q[N], dist[N];
bool st[N];
int gcd(int a, int b) // 欧几里得算法
{
return b ? gcd(b, a % b) : a;
}
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void spfa() // 求1号点到n号点的最短路距离
{
int hh = 0, tt = 0;
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
q[tt ++ ] = 1;
st[1] = true;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q[tt ++ ] = j;
if (tt == N) tt = 0;
st[j] = true;
}
}
}
}
}
int main()
{
n = 2021;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ )
for (int j = max(1, i - 21); j <= min(n, i + 21); j ++ )
{
int d = gcd(i, j);
add(i, j, i * j / d);
}
spfa();
printf("%d\\n", dist[n]);
return 0;
}
答案:10266837
时间显示

比赛时忘了1s等于多少ms,还好电脑自带计算器里有时间的进制关系(狗头🐕)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
int main()
{
LL n;
cin >> n;
n /= 1000;
n %= 86400;
int h = n / 3600;
n %= 3600;
int m = n / 60;
int s = n % 60;
printf("%02d:%02d:%02d\\n", h, m, s);
return 0;
}
G砝码称重

背包问题
自己对dp真的不熟。。五一要好好练练dp
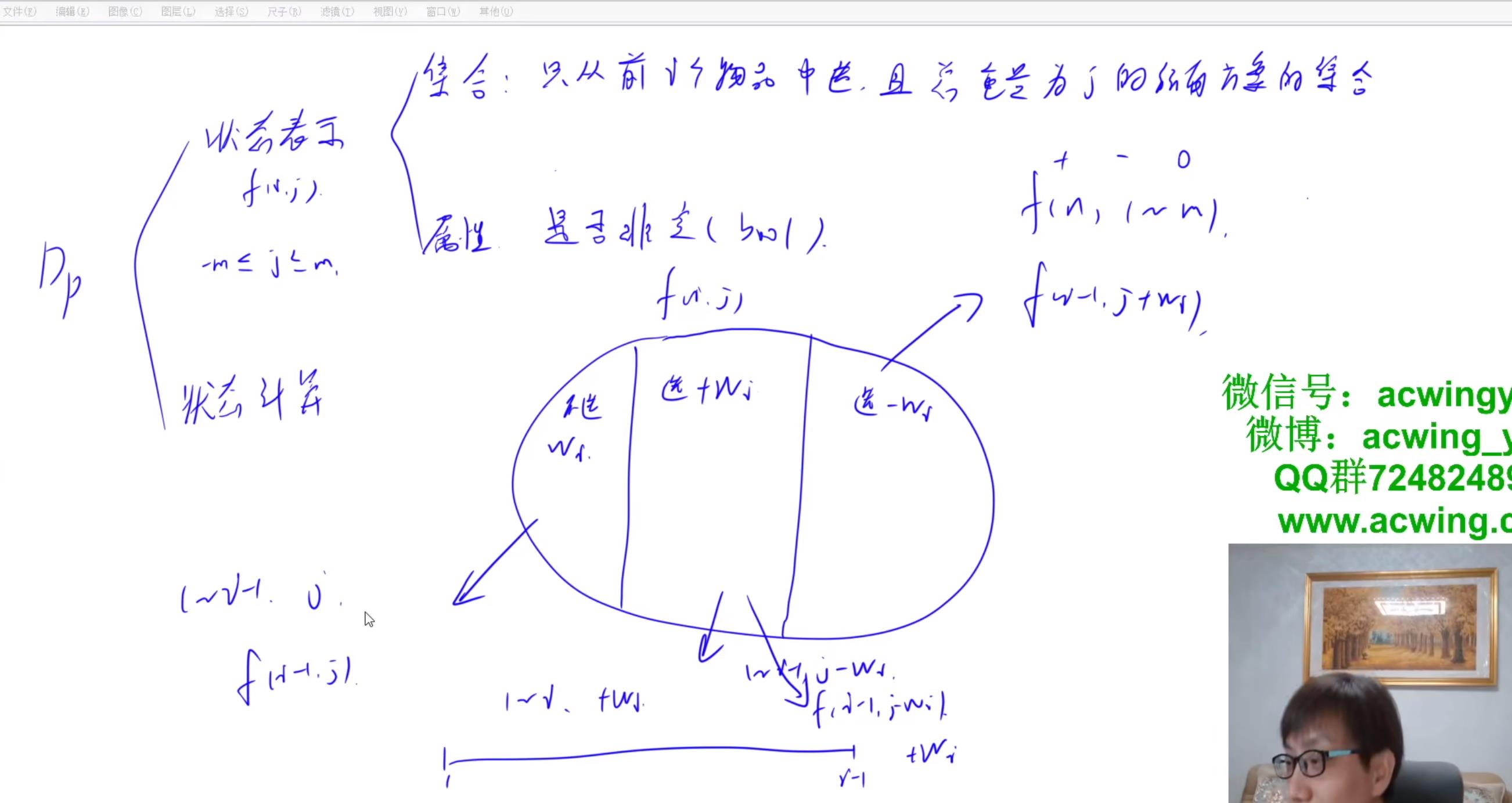
对于每个砝码他有三个选择,称的左侧,右侧和不放,
我们设dp[i][j]表示前i个物品中,总质量为j的情况是否存在,dp为bool型
对于第j个物品,我们说了有三种选择,所以我们可以得到转移方程:
分别对应不选,放左侧,放右侧
dp[i][j]|=dp[i-1][j]
dp[i][j]|=dp[i-1][j-w[i]]
dp[i][j]|=dp[i-1][j+w[i]]
按照题目要求j-w[i]最小为-m,数组不能用负下标,所以我们加一个偏移量B,保证数组下标都为非负
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, M = 200010, B = M / 2;
int n, m;
int w[N];
bool f[N][M];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]), m += w[i];
f[0][B] = true;
for (int i = 1; i <= n; i ++ )
for (int j = -m; j <= m; j ++ )
{
f[i][j + B] = f[i - 1][j + B];
if (j - w[i] >= -m) f[i][j + B] |= f[i - 1][j - w[i] + B];
if (j + w[i] <= m) f[i][j + B] |= f[i - 1][j + w[i] + B];
}
int res = 0;
for (int j = 1; j <= m; j ++ )
if (f[n][j + B])
res ++ ;
printf("%d\\n", res);
return 0;
}
H杨辉三角形

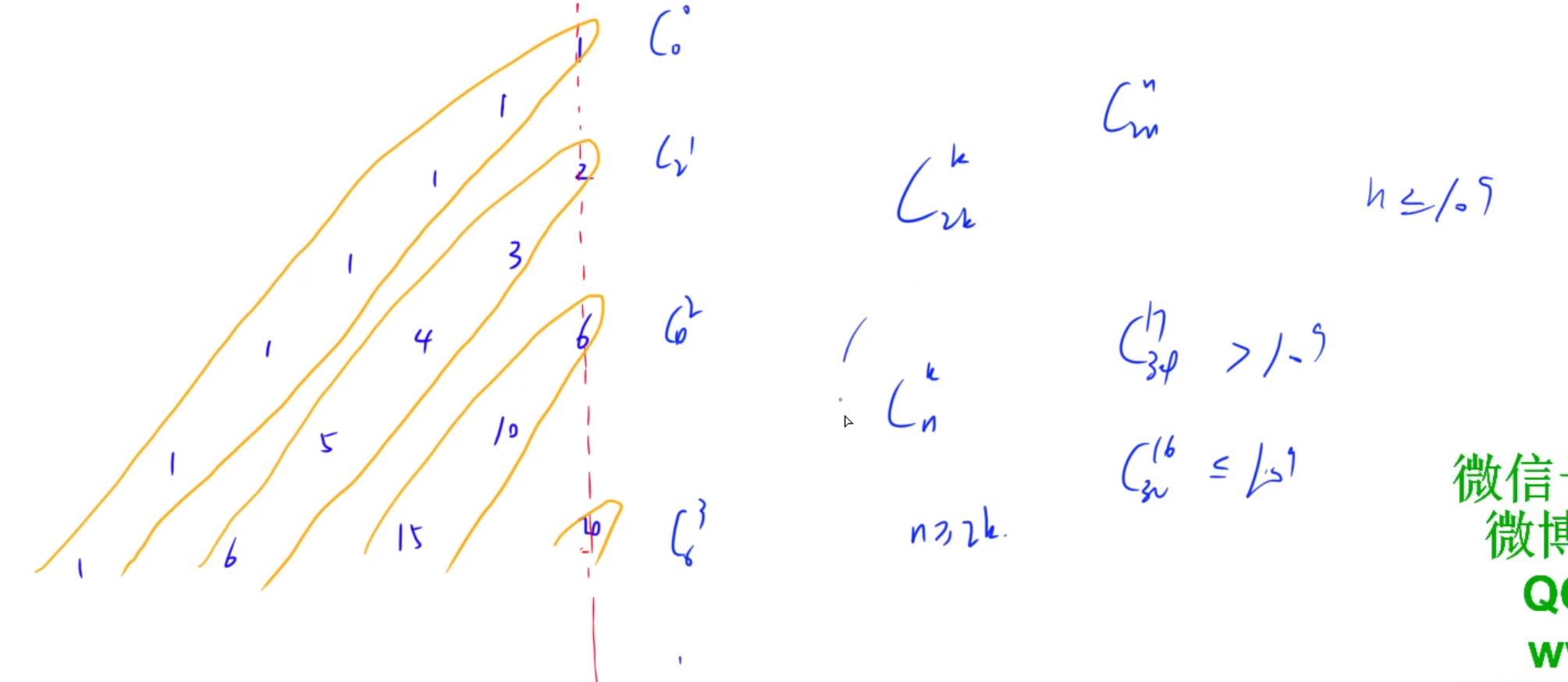
因为杨辉三角形左右对称,所以我们只考虑左半部分
我们进行枚举可以看出,斜列的数量不会超过20个,所以枚举每一个斜列,每个斜列的第一个元素也是递增排列且有关系(第一个斜列的首元素为C(1,0),第二个为C(1,2),第三个为C(2,4),…C(x,2x)),斜列内的元素是递增排列的,且大小都有公式关系(比如第3个斜列,第一个元素是C(2,4),第二个元素是C(2,5),然后是C(2,6)…),然后二分找具体位置
如果第C(r,k)是我们要找的元素,他的位置就是r * (r + 1) / 2 + k + 1
思维题
妙啊,当时写了一个半暴力,真想不到
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
int n;
LL C(int a, int b)
{
LL res = 1;
for (int i = a, j = 1; j <= b; i --, j ++ )
{
res = res * i / j;
if (res > n) return res;
}
return res;
}
bool check(int k)
{
//C(a,b)
//a>=2b,二分a
LL l = k * 2, r = n;
while (l < r)
{
LL mid = l + r >> 1;
if (C(mid, k) >= n) r = mid;
else l = mid + 1;
}
if (C(r, k) != n) return false;
cout << r * (r + 1) / 2 + k + 1 << endl;
return true;
}
int main()
{
cin >> n;
for (int k = 16; ; k -- )
if (check(k))
break;
return 0;
}
双向排列
J括号序列

肯定是dp,但是我不会。。。等会了再更新
以上是关于第十二届蓝桥杯C++赛后感的主要内容,如果未能解决你的问题,请参考以下文章