matlab改进遗传算法求解带时间窗的路径优化问题

Posted 2021-05-07 张叔zhangshu

改进方法

对初始化进行编写时，不在采用随机产生编码的方式，而是根据车辆的最大载重的限制下，进行编码，如若选择的下一个点超过了最大载重则把下一个点分配给下一辆车，对已经选择的点根据时间窗的开始或者结束对点进行排序，例如，根据最早时间窗，对选择的点进行从小到大排序。
这样产生的解保证了初始种群得到的解时较优的，在后续迭代过程中能够更快的得到最优解。

产生初始种群新的编码代码

function [init_vc] = init(cusnum,a,demands,cap)
j=ceil(rand*cusnum);                    %从所有顾客中随机选择一个顾客
k=1;                                    %使用车辆数目，初始设置为1
init_vc=cell(k,1);
% 按照如下序列，遍历每个顾客，并执行以下步骤
if j==1
    seq=1:cusnum;
elseif j==cusnum
    seq=[cusnum,1:j-1];
else
    seq1=1:j-1;
    seq2=j:cusnum;
    seq=[seq2,seq1];                      
end
%% 开始遍历
route=[];       %存储每条路径上的顾客
load=0;         %初始路径上在仓库的装载量为0
i=1;
while i<=cusnum
    %如果没有超过容量约束，则按照左时间窗大小，将顾客添加到当前路径
    %%
    if (load+demands(seq(i))<=cap)&&(size(route,1)<=20)    %%%%自己家的条件****************   
    %%  
        load=load+demands(seq(i));          %初始在仓库的装载量增加
        %如果当前路径为空，直接将顾客添加到路径中
        if isempty(route)
            route=[seq(i)];
        %如果当前路径只有一个顾客，再添加新顾客时，需要根据左时间窗大小进行添加
        elseif length(route)==1
            if a(seq(i))<=a(route(1))
                route=[seq(i),route];   
            else
                route=[route,seq(i)];
            end
        else
            lr=length(route);       %当前路径长度,则有lr-1对连续的顾客
            flag=0;                 %标记是否存在这样1对顾客，能让seq(i)插入两者之间
            %遍历这lr-1对连续的顾客的中间插入位置
            for m=1:lr-1
                if (a(seq(i))>=a(route(m)))&&(a(seq(i))<=a(route(m+1)))
                    route=[route(1:m),seq(i),route(m+1:end)];
                    flag=1;
                    break
                end
            end
            %如果不存在这样1对顾客，能让seq(i)插入两者之间，也就是flag=0，则需要将seq(i)插到route末尾
            if flag==0
                route=[route,seq(i)];
            end
        end
        %如果遍历到最后一个顾客，则更新init_vc，并跳出程序
        if i==cusnum
            init_vc{k,1}=route;
            break
        end
        i=i+1;
    else   %一旦超过车辆载货量约束，则需要增加一辆车
        %先储存上一辆车所经过的顾客
        init_vc{k,1}=route;
        %然后将route清空，load清零,k加1
        route=[];
        load=0;
        k=k+1;
    end
end
end

如上是新的编码方式，
得到的最优解过程和结果如下：


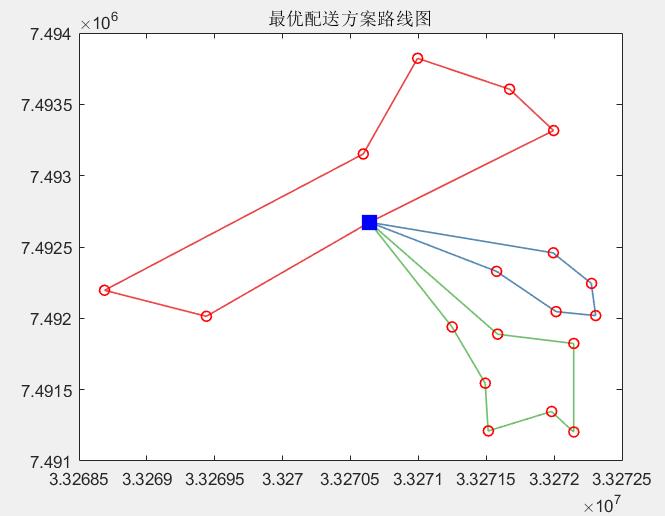
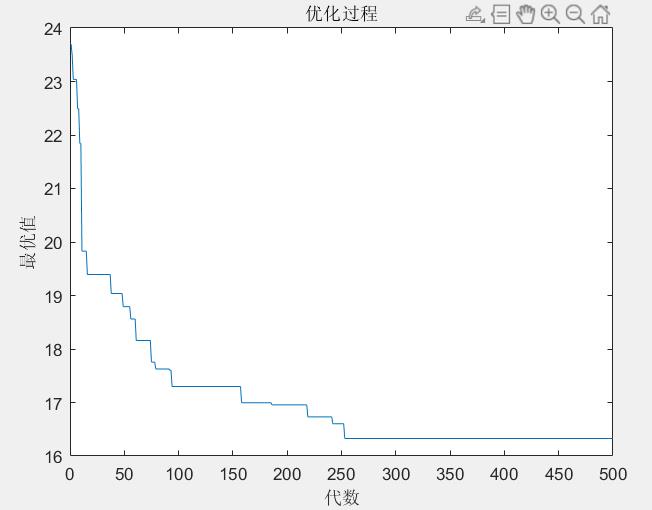
在迭代初始并未出现超载的情况，所以在最开始代码就较优，能够更快的得到最优解。
最优解:
车辆使用数目：3，车辆行驶总距离：16.328

配送路线1：0->16->14->13->12->17->0
配送路线2：0->5->2->1->3->6->4->0
配送路线3：0->7->9->11->10->15->8->18->0

如需代码货代写请+VX：zzs1056600403