数据结构复习笔记——树的基本概念及结构

Posted 2021-05-07 sjp11

前言

数据结构

• 前言
• 树的概念及结构
• • 1.什么是树？
  • 2.树的基本概念
  • 3.树的表示方法
  • 4.树的实际应用
• 二叉树的概念及结构
• • 1.概念
  • 2.特殊的二叉树
  • • 2.1满二叉树
    • 2.2完全二叉树
    • 2.3普通二叉树的性质
• 题目
• 完！

树的概念及结构

在我们了解二叉树之前，我们需要先了解树的概念及其性质

1.什么是树？

现实生活中的树是这样子的，它由很多树枝组成；

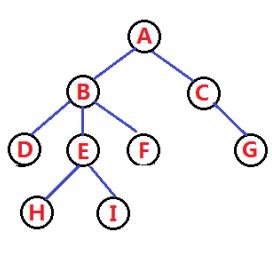
而在数据结构中，树是长这样子的


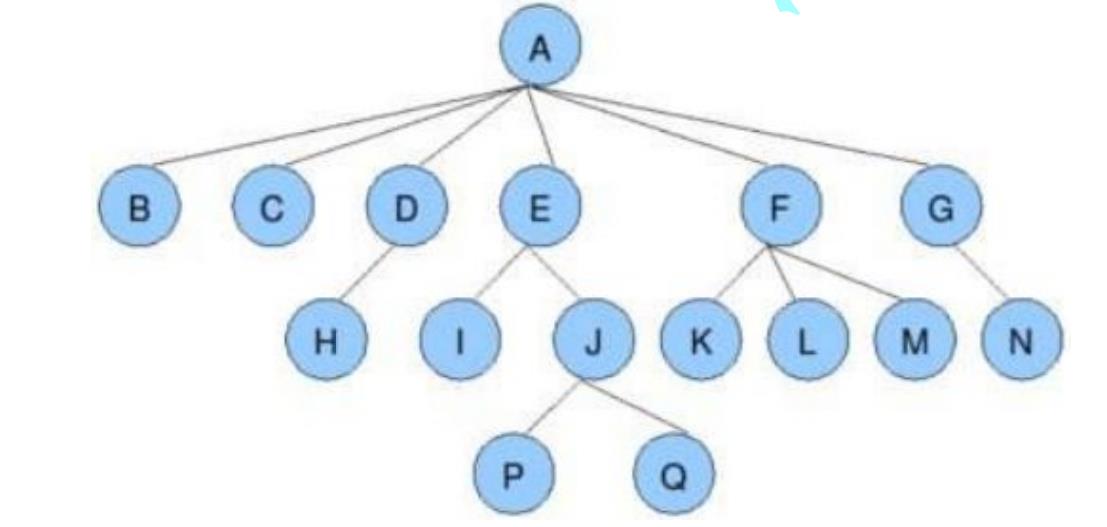
你可能会感到很奇怪，数据结构的树怎么向下长的，其实，在数据结构中，把它叫做树的原因是它看起来像一颗倒挂的树，也就是说它的根是朝上的，而叶朝下的。

2.树的基本概念

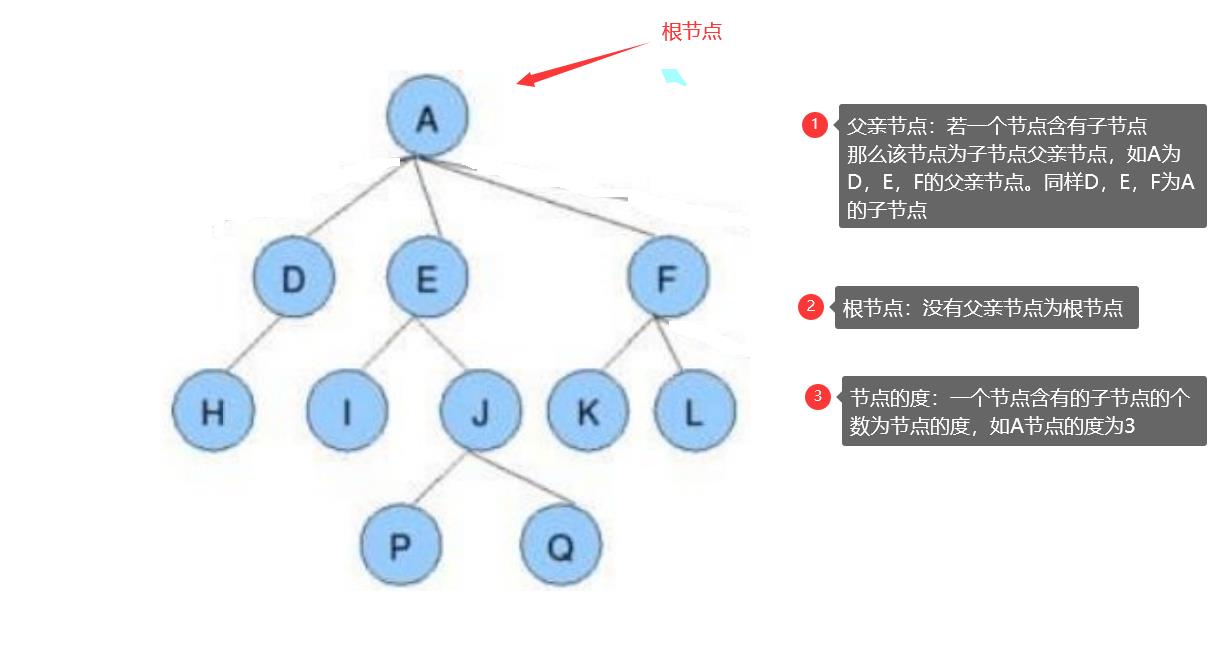
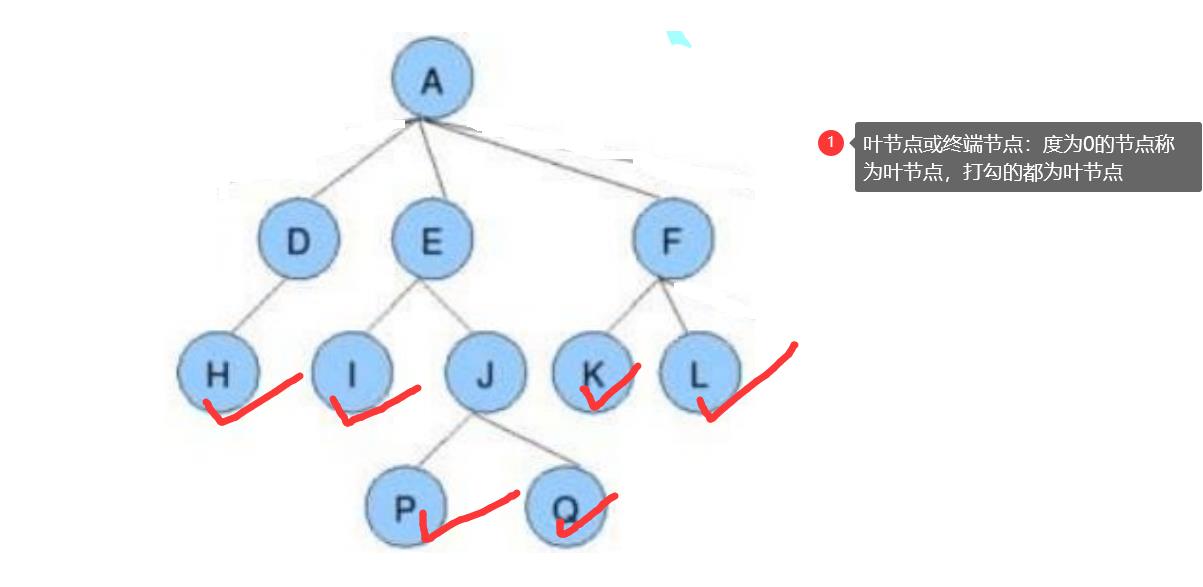
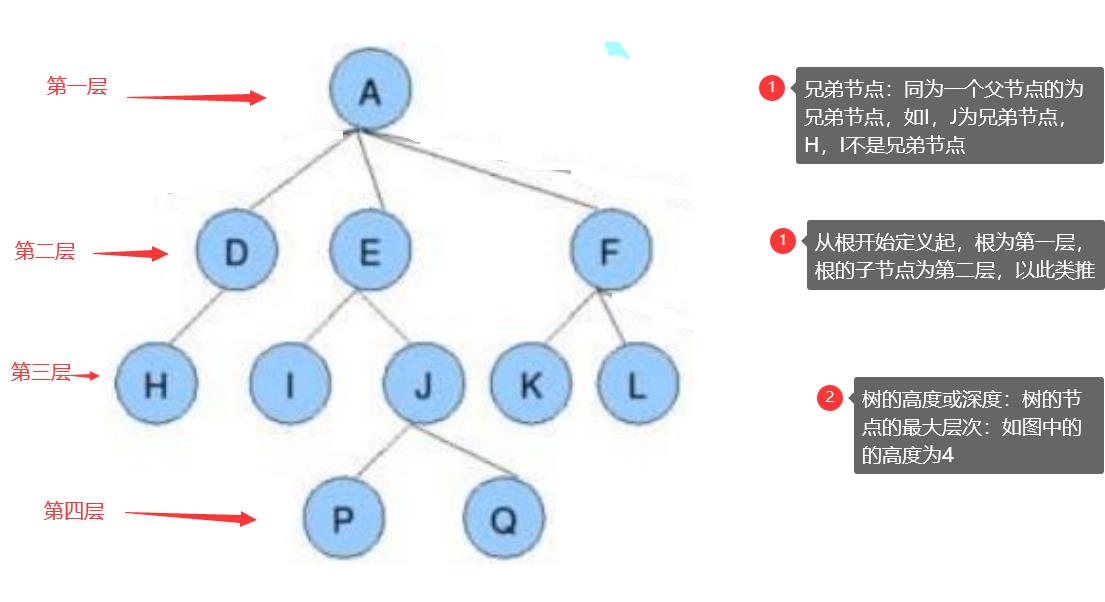
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
森林：由m（m>0）棵互不相交的树的集合称为森林；
堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先

请问下面这些都是树吗？

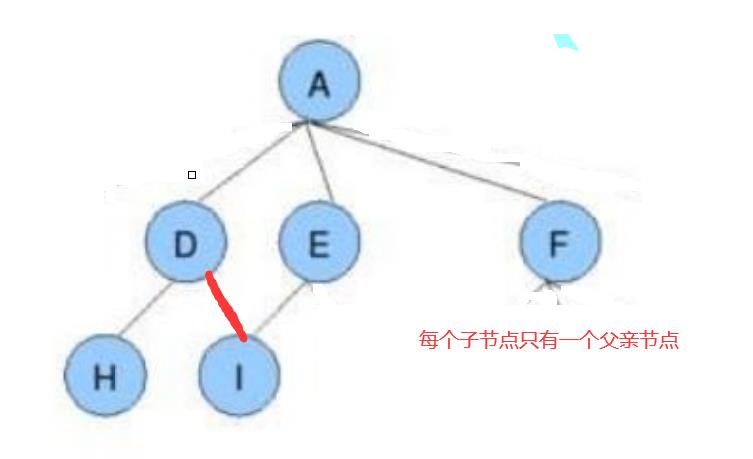
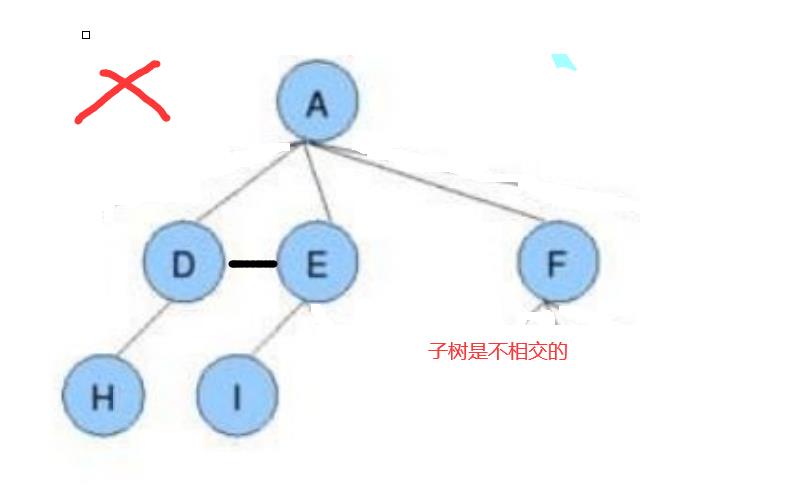
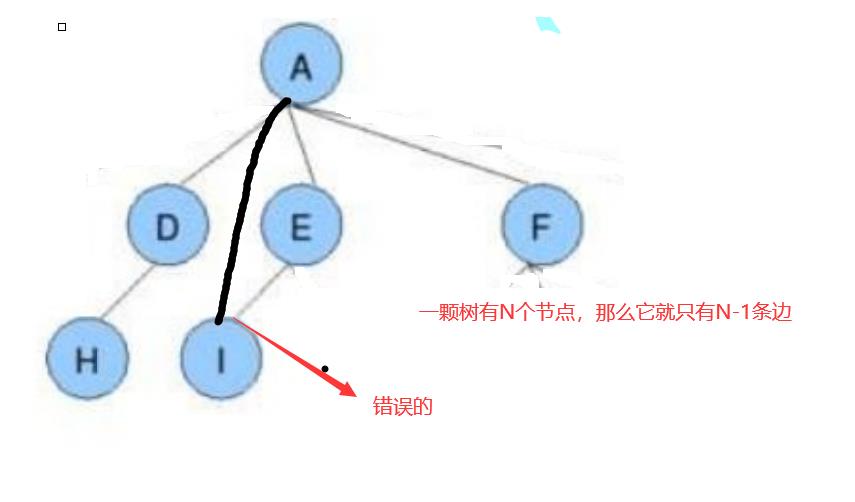
3.树的表示方法

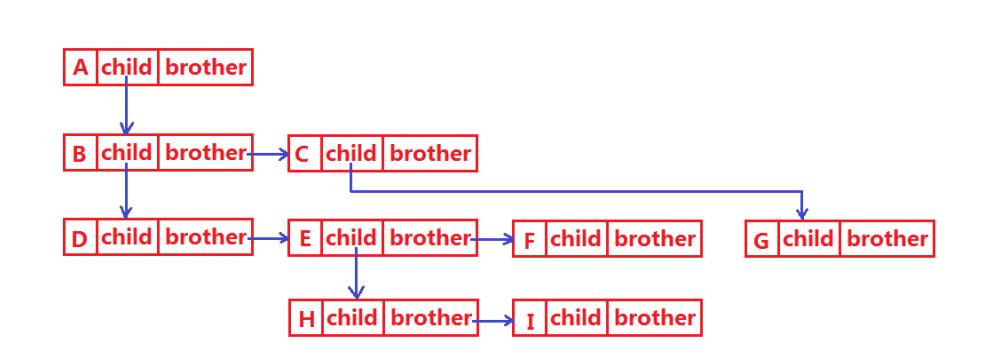
树有很多表示的方法，其中最常见和常用的是孩子兄弟表示法

通过孩子兄弟表示法，我们可以把上面的结构表示如下面这种：

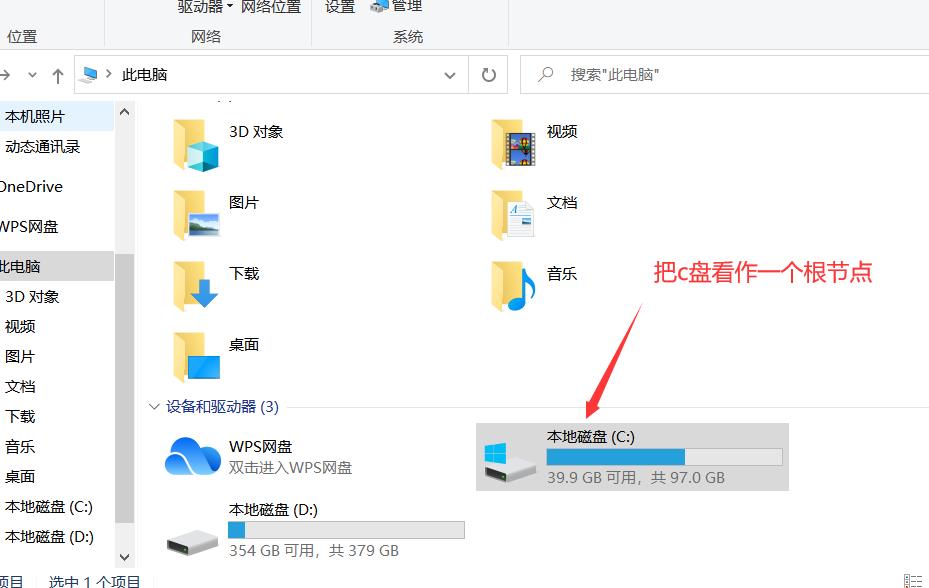
4.树的实际应用

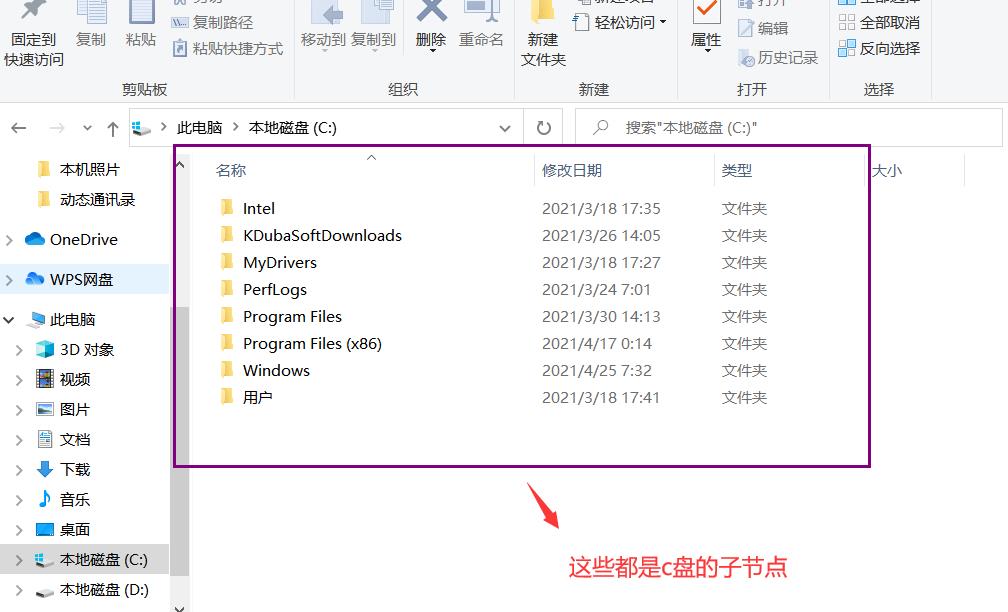
树的实际应用，最常见的是文件系统，先把其中c个盘看作以一个根节点，然后点进去就有很多的文件，这些文件就是c盘的子节点，每个文件中也含有许多子文件，这样的结构就是树的结构。

二叉树的概念及结构

1.概念

二叉树中的节点最多有两个子节点

现实中的二叉树是这样子的

数据结构中的二叉树,只要每个节点中的子节点都不超过二都为二叉树：

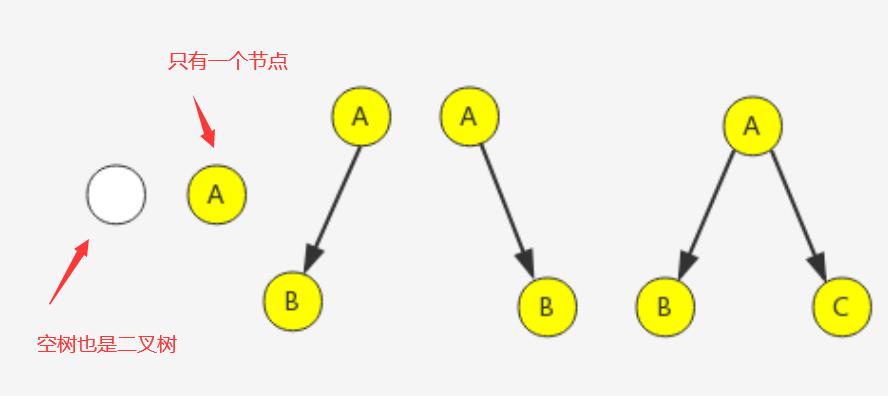
2.特殊的二叉树

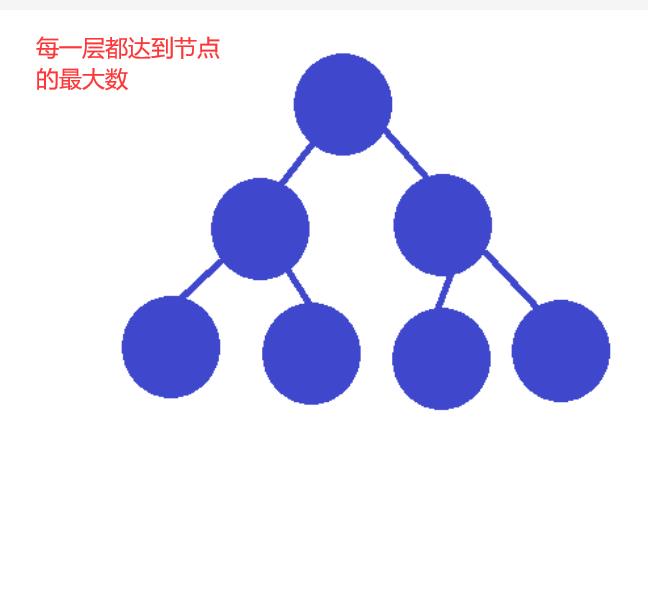
2.1满二叉树

满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是
说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。

满二叉树的性质： 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=Log2(n+1). (ps：Log2(n+1)是log以2为
底，n+1为对数)

2.2完全二叉树

完全二叉树:对于有一颗n层的二叉树，前n-1层的节点都是满的，第n层可以不满，但节点必须都是从左向右排序。

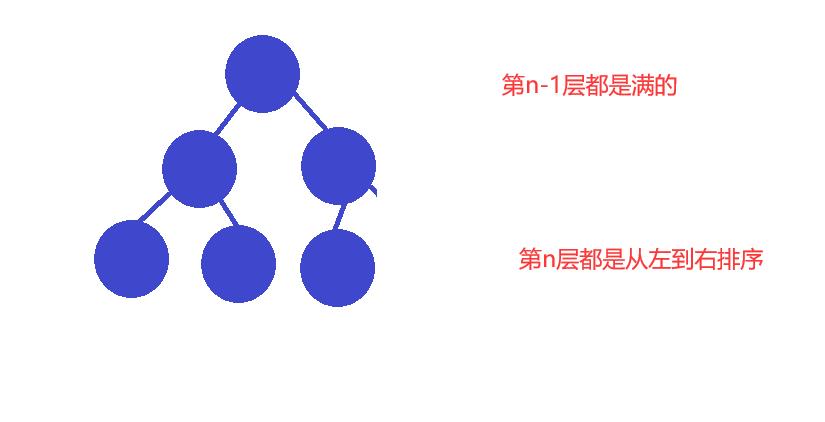
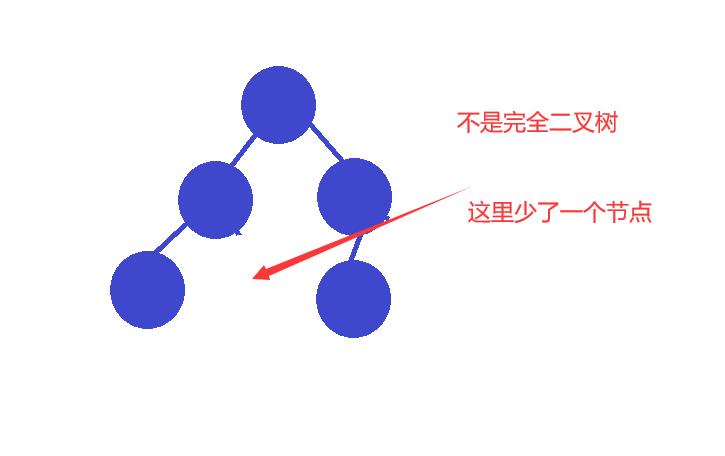
完全二叉树的性质：
性质1：

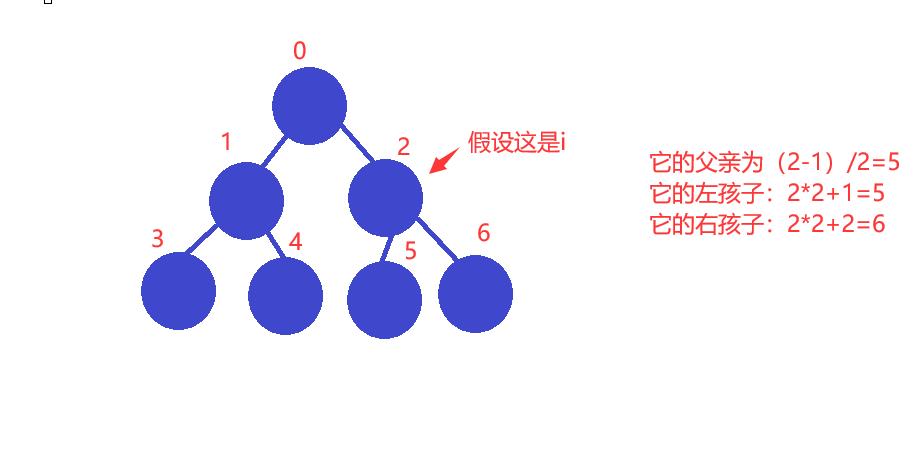
对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对
于序号为i的结点有：
a.i>0,则它的父亲节点为,(i-1)/2
b.若2i+1<n,则它的左孩子:2i+1,因为2i+1>=n则没有左孩子
c.若2i+2<n，右孩子序号：2i+2，2i+2>=n则无右孩子

性质2：

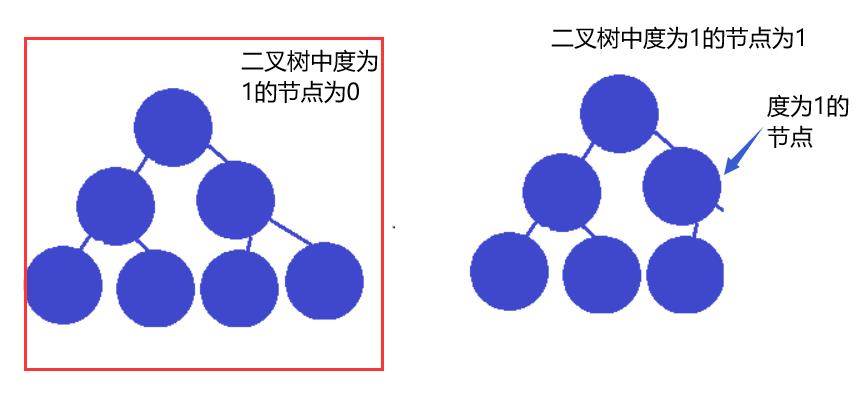
完全二叉树中的度为1的节点最多为1.

2.3普通二叉树的性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有 2^(i-1) 个结点.
2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h- 1.
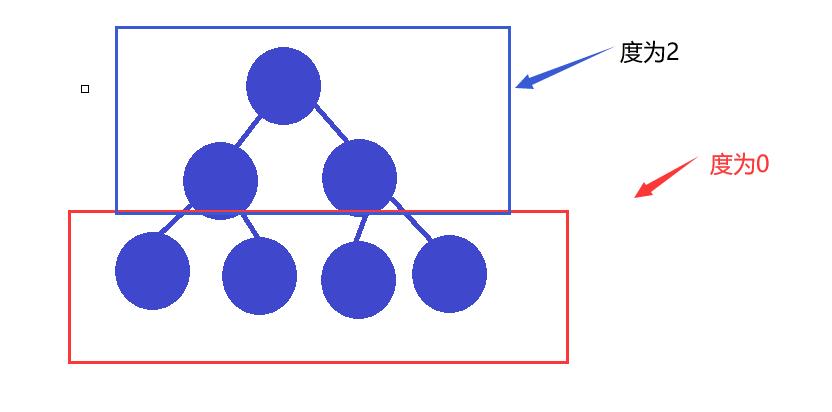
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0＝n2＋1
   

题目

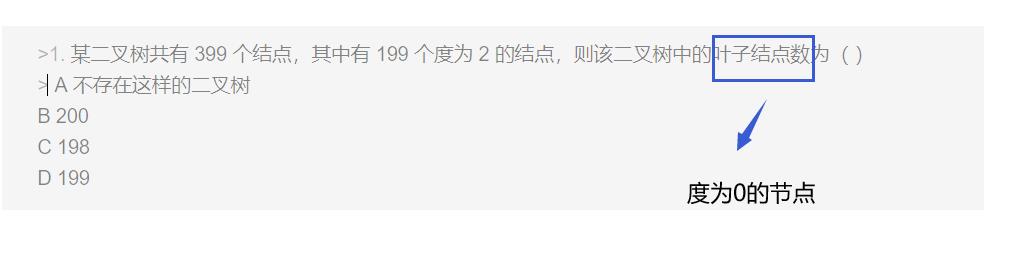
1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）
   A 不存在这样的二叉树
   B 200
   C 198
   D 199

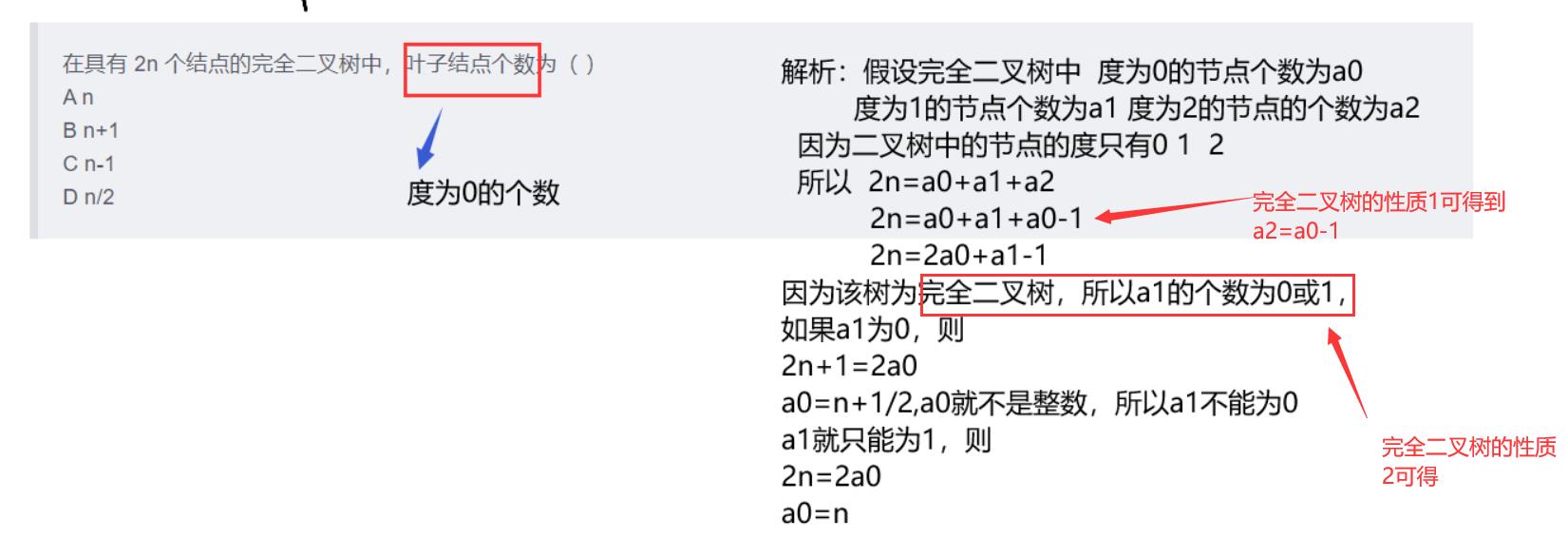
2.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）
A n
B n+1
C n-1
D n/2

解析：

3.一棵完全二叉树的节点数位为531个，那么这棵树的高度为（ ）
A 11
B 10
C 8
D 12

解析：一颗高度为k层的完全二叉树中的节点的个数等于在 （深度为k-1层满二叉树的节点个数，深度为k层满二叉树的节点的个数]的区间内，举个例子：
假设为高度为3的完全二叉树，则它的节点个数在（3, 7]的区间，下面这些都是深度为3的完全二叉树

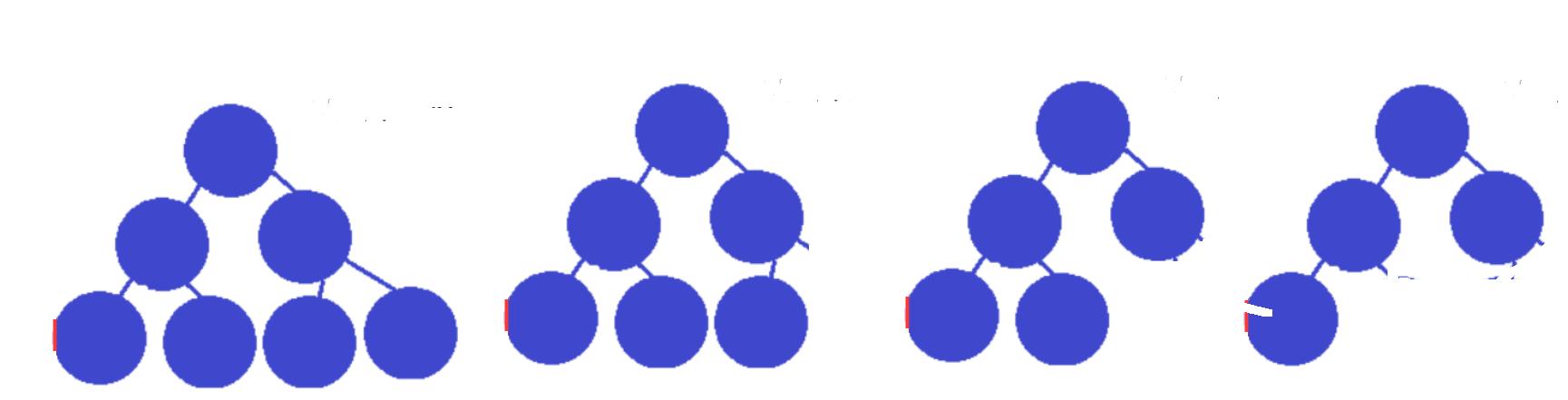
所以
高度为11的完全二叉树的节点个数在(1023,2047]的区间
高度为10的完全二叉树的节点个数在（511,1023]的区间
高度为8的完全二叉树的节点个数在(127,255]的区间
高度为8的完全二叉树的节点个数在(2047,4095]的区间
所以531显然在高度为10的完全二叉树中

1.B 2.A 3.B

完！