TensorFlow2 入门指南 | 06 TensorFLow2 高阶操作汇总
Posted AI 菌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了TensorFlow2 入门指南 | 06 TensorFLow2 高阶操作汇总相关的知识,希望对你有一定的参考价值。
前言:
本专栏在保证内容完整性的基础上,力求简洁,旨在让初学者能够更快地、高效地入门TensorFlow2 深度学习框架。如果觉得本专栏对您有帮助的话,可以给一个小小的三连,各位的支持将是我创作的最大动力!
系列文章汇总:TensorFlow2 入门指南
Github项目地址:https://github.com/Keyird/TensorFlow2-for-beginner
一、合并与分割
(1)合并
合并是指将多个张量在某个维度上合并为一个张量。在 TensorFlow 中,可以通过 tf.concat()和tf.stack()进行合并操作。
- tf.concat(tensors, axis) 有两个参数,其中 tensors 保存了所有需要合并的张量,axis 指定需要合并的维度,例如:
# 随机生成a,b两个张量
a = tf.random.normal([5, 40, 10])
b = tf.random.normal([3, 40, 10])
# 在第一个维度合并,c最终的shape为:[8, 40, 10]
c = tf.concat([a, b], axis=0)
如果需要在合并数据时,产生一个新的维度,那就需要用堆叠操作:tf.stack()
- tf.stack(tensors, axis) 可以合并多个张量tensors,其中 axis指定插入新维度的位置。当axis ≥ 0时,在 axis 之前插入;当axis < 0时,在 axis 之后插入新维度。如下图所示,不同的 axis 值代表的插入位置如下:
还是通过上面的例子,通过tf.stack()得到不同的合并结果:
a = tf.random.normal([3, 40, 10])
b = tf.random.normal([3, 40, 10])
c = tf.stack([a, b], axis=0)
print(c.shape) # 输出的shape为:【2,3,40,10】
需要注意的是:使用 tf.stack() 进行合并时,a、b 的 shape 必须一样。
(2)分割
合并操作的逆过程就是分割,是指将一个张量分拆为多个张量。在TensorFlow2中,可以通过 tf.unstack() 和 tf.split() 进行分割。
- tf.unstack(x, axis) 会将张量x在某个维度上全部 按长度为 1 的方式分割,例如:
x = tf.random.normal([8,28,28,3])
result = tf.unstack(x,axis=0)
通过tf.unstack分割后,维度由 [8,28,28,3] 变为 [28,28,3]。准确来说变成了10个维度是 [28,28,3] 的张量。
- tf.split(x, axis, num_or_size_splits) 更加灵活,可以通过设置 num_or_size_splits 将张量维度分割的更细致。比如,要将 shape 为 [8, 28, 28, 3] 的张量按第一维度切分成3份,每份长度分别为:2,4,2
x = tf.random.normal([8,28,28,3])
result = tf.split(x, axis=0, num_or_size_splits=[2,4,2])
二、 数据统计
(1)向量范数
向量范数是表征向量“长度”的一种度量方法,在神经网络中,常用来表示张量的权值大小,梯度大小等。常用的向量范数有:
- L1 范数,定义为向量𝒙的所有元素绝对值之和:
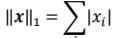
- L2 范数,定义为向量𝒙的所有元素的平方和,再开根号:
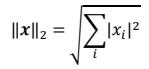
- ∞ − 范数,定义为向量𝒙的所有元素绝对值的最大值:
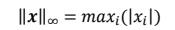
对于矩阵、张量,同样可以利用向量范数的计算公式,等价于将矩阵、张量打平成向量后计算。在 TensorFlow 中,可以通过 tf.norm(x, ord)求解张量的 L1, L2, ∞等范数,其中参数 ord 指定为 1,2 时计算 L1, L2 范数,指定为 np.inf 时计算∞ −范数:
x = tf.ones([2,2])
tf.norm(x, ord=1)
tf.norm(x, ord=2)
tf.norm(x, ord=np.inf)
(2)最大值、最小值
通过 tf.reduce_max, tf.reduce_min 可以求解张量在某个维度上的最大、最小值,也可以求全局最大、最小值。
考虑 shape 为 [4,10] 的张量,其中第一个维度代表样本数量,第二个维度代表了当前样本分别属于 10 个类别的概率,需要求出每个样本的概率最大值、最小值为:
x = tf.random.normal([4,10])
tf.reduce_max(x, axis=1) # 统计概率维度上的最大值(第2个维度)
tf.reduce_min(x,axis=1) # 统计概率维度上的最小值(第2个维度)
(3)和、均值
tf.reduce_mean, tf.reduce_sum 可以求解张量在某个维度上的均值、和,也可以求全局最均值、和信息。
同样利用上面的例子,求出每个样本的概率的均值以及和:
tf.reduce_mean(x,axis=1) # 统计概率维度上的均值(第2个维度)
tf.reduce_sum(out,axis=-1)# 统计概率维度上的和(第2个维度)
注意:当不指定 axis 参数时,tf.reduce_* 函数会求解出全局元素的最大、最小、均值、和。
(4)最大值、最小值索引
通过 tf.argmax(x, axis),tf.argmin(x, axis) 可以求解在 axis 轴上,x 的最大值、最小值所在的索引号。比如求输出向量out在概率维度上(第二维度)的最大值、最小值索引:
pred_max_index = tf.argmax(out, axis=1) # 最大值索引(第二维度)
pred_min_index = tf.argmin(out, axis=1) # 最小值索引 (第二维度)
三、张量比较
为了计算分类任务的准确率等指标,一般需要将预测结果和真实标签比较,统计结果中正确的数量来计算准确率。
(1)tf.equal()
考虑 100 个样本、10类的预测结果,先选取每个向量维度上的最大值索引,即预测值(比如第一个样本的概率最大索引是5,表示预测的结果是第5类)
out = tf.random.normal([100,10]) # 随机生成一个张量,用来模拟输出结果
out = tf.nn.softmax(out, axis=1) # 输出转换为概率值,缩放到0-1,且概率和为1
pred = tf.argmax(out, axis=1) # 选取预测值(概率维度上的最大值),得到的是长度为100的向量
模拟100个真实标签,采用上节讲的均匀分布tf.random.uniform()来创建长度为100,值属于[0,9]区间的向量:
y = tf.random.uniform([100],dtype=tf.int64,maxval=10) # 标签
接下来,通过 tf.equal(pred, y) 可以比较这 2个张量是否相等。tf.equal()函数返回布尔型的张量比较结果:
out = tf.equal(pred,y) # 预测值与真实值比较
注意:tf.math.equal(a, b) 与 tf.equal(a, b) 用法一样
(2)tf.cast()
由于 tf.equal() 返回的是bool型的张量,所以要统计张量中 True 元素的个数,即可知道预测正确的个数。为了达到这个目的,我们需要通过tf.cast(x, type)将布尔型转换为整形张量:
out = tf.cast(out, dtype=tf.float32) # 布尔型转 int 型
于是,比较结果都转换成0和1了,然后再求和,统计其中 1 的个数,即预测正确的样本个数:
correct_num = tf.reduce_sum(out) # 统计 True 的个数
假设最终得到的correct_num=95,那么本次预测数据的准确度是:95/100=95%
四、张量排序
(1)tf.sort()
tf.sort() 能对列表中的元素按照大小进行排序,默认情况下进行升序排列,关键字 DESCENDING 指定降序排序。
先创建一打乱后的列表:
# 创建列表 [0,1,2,3,4],并打乱顺序
a = tf.random.shuffle(tf.range(5))
print("打乱后的列表:", a)
使用tf.sort()对其进行升序和降序排列:
# 升序
b = tf.sort(a)
print("升序排列后的列表:", b)
# 降序
c = tf.sort(a, direction="DESCENDING")
print("降序排列后的列表:", c)
输出结果:

(2)tf.argsort()
tf.argsort(a) 返回按照升(降)序排列的各元素在原列表a中的索引号。通过这种方式,可以方便地找到原数组中最大值或者最小值的索引值。
arise_index = tf.argsort(a)
print("升序列表各元素在原列表a中的索引号:", arise_index)
descend_index = tf.argsort(a, direction="DESCENDING")
print("降序列表各元素在原列表a中的索引号:", descend_index)
输出结果:

分析:该结果表明,元素 0、1、2、3、4 在原数组 a=[4,0,2,1,3] 中的索引号分别是:1、3、2、4、0;同理,元素 4、3、2、1、0 在原数组 a=[4,0,2,1,3] 中的索引号分别是:0、4、2、3、1。
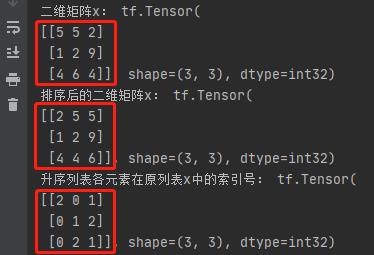
以上是对一维向量的排序结果,采用 tf.sort() 和 tf.argsort() 也能对二维数组进行排序操作,作用如下:
""" 对二维数组进行排序 """
x = tf.random.uniform([3, 3], maxval=10, dtype=tf.int32)
print("二维矩阵x:", x)
x_arise = tf.sort(x)
print("排序后的二维矩阵x:", x_arise)
x_arise_index = tf.argsort(x)
print("升序列表各元素在原列表x中的索引号:", x_arise_index)
输出结果:
(3)tf.gather()
tf.gather(a, index) 通过升(降)序索引,可将输入列表 a 还原成升(降)序列表:
Arise_List = tf.gather(a, arise_index)
print("升序列表:", Arise_List)
DES_List = tf.gather(a, descend_index)
print("降序列表:", DES_List)
程序输出:

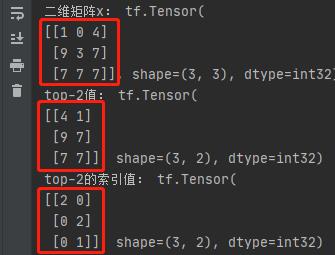
(4)tf.math.top_k()
在 TensorFlow2 中,通过 tf.math.top_k() 、values、indices 可以很轻松地获取数组的top-k值以及他们的索引值:
""" 获取top-K的数值以及索引 """
x = tf.random.uniform([3, 3], maxval=10, dtype=tf.int32)
print("二维矩阵x:", x)
res = tf.math.top_k(x, 2)
print("top-2值:", res.values)
print("top-2的索引值:", res.indices)
程序输出:
五、填充与复制
(1)填充
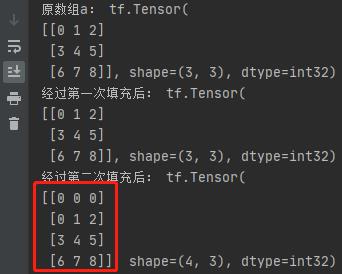
对二维矩阵进行填充:
在 TensorFlow2 中,可通过 tf.pad(x, [[上, 下], [左, 右]]) 指定在矩阵 x 的上下左右边上填充一行(列)0 元素:
""" 填充 Padding """
a = tf.reshape(tf.range(9), [3, 3])
print("原数组a:", a)
b = tf.pad(a, [[0, 0], [0, 0]])
print("经过第一次填充后:", b)
c = tf.pad(a, [[1, 0], [0, 0]])
print("经过第二次填充后:", c)
程序输出:
更常见的,会对四维张量进行填充操作:
比如,下面对图像张量 [4,28,28,3] 进行填充,4是batch_size,一般不需要填充,通常情况是对图像的size 28x28 进行填充,现在对 28x28 向上下左右各填充两行(列)0,其操作如下:
""" 对四维张量进行填充 """
x = tf.random.normal([4, 28, 28, 3])
print("x.shape:",x.shape)
x_pad = tf.pad(x, [[0, 0], [2, 2], [2, 2], [0, 0]])
print("x_pad.shape:", x_pad.shape)
填充前后,张量的 shape 分别如下所示:

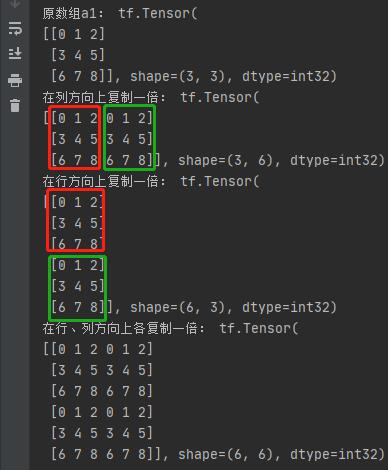
(2)复制
在 TensorFlow2 中,通过 tf.tile() 选择性地在行或者列的维度上进行复制,其操作如下所示:
""" 复制 """
a1 = tf.reshape(tf.range(9), [3, 3])
print("原数组a1:", a1)
b1 = tf.tile(a1, [1, 2])
print("在列方向上复制一倍:", b1)
c1 = tf.tile(a1, [2, 1])
print("在行方向上复制一倍:", c1)
d1 = tf.tile(a1, [2, 2])
print("在行、列方向上各复制一倍:", d1)
在行、列上进行复制操作后,得到的矩阵分别如下:
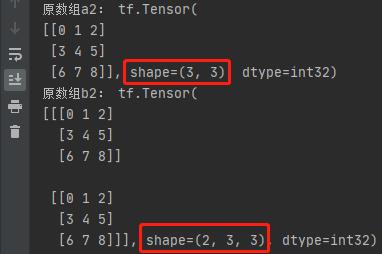
在 TensorFlow2 中,通过 tf.tile() 不仅可以在同一维度内进行复制,也可以通过复制扩充张量的维度,比如将shape为[3,3]的矩阵进行维度上的复制,使其变为shape为[2,3,3]的张量:
# 维度上的复制:[3,3] -> [2,3,3]
a2 = tf.reshape(tf.range(9), [3, 3])
print("原数组a2:", a2)
a2 = tf.expand_dims(a2, axis=0) # 增加一个维度
b2 = tf.tile(a2, [2, 1, 1])
print("原数组b2:", b2)
输出结果:
六、数据限幅
(1)tf.maximum()
在 TensorFlow2 中,可以通过 tf.maximum(x, low) 实现数据的下限幅:𝑥 ∈ [low, +∞);示例如下:
a = tf.range(9)
print("a:", a)
b = tf.maximum(a, 2) # 设置下限是2
print("下限限制为2后:", b)
如下是限制前后的向量对比:

通过 tf.maximum() 限制下限,还可以实现基本的激活函数ReLU:
def relu(x):
return tf.maximum(x, 0)
x = a - 5
print("x:", x)
y = relu(x)
print("y:", y)
对ReLU函数输入x,可以看到输出的y满足激活函数的特性:

PS:ReLU是常见的激活函数的一种,其函数模型如下:

在 TensorFlow2 中,可以直接调用 tf.nn.relu() 来实现以上功能。
(2)tf.minimum()
在 TensorFlow 中,也可以通过 tf.minimum(x, high) 实现数据的上限幅:𝑥 ∈ (−∞, high],举例如下:
b1 = tf.minimum(a, 6)
print("上限限制为6后:", b1)
设置上限为6后,向量限幅后变为:

(3)tf.clip_by_value()
如果想同时对数据设置上限和下限,那么可以使用 clip_by_value(x, low, high) 来将数据限制在 [low, high] 之间。例如下面要将向量a的数据限制在5~8之间:
b2 = tf.clip_by_value(a, 5, 8)
print("下限设置为5,上限设置为8后:", b2)
下限设置为5,上限设置为8后:

七、其它操作
(1)tf.gather()
通过 tf.gather(x, [indexes], axis) 可以实现根据索引号收集数据的目的,其中 x 表示输入张量,[indexes]表示要获取的数据索引,axis表示要获取的维度。比如下面通过 tf.gather 获取第0至第3张图片:
# [b, w, h, c]
images = tf.random.normal([8, 28, 28, 3])
# 取第0至第3张图片
images_0_3 = tf.gather(images, [0, 1, 2, 3], axis=0)
print("images_0_3的shape:", images_0_3.shape)
对于0~3这种连续索引的情况,也可直接通过索引实现,如下所示:
# 也可通过索引来实现
images_0_3 = images[:4,...]
print("images_0_3的shape:", images_0_3.shape)
对于 tf.gather() 来说,其特殊之处,在于对于非连续索引时操作更为方便。比如,加下来我们要对第0至3张图片的第0和第2通道进行数据提取:
# 对第0和第2通道进行提取
out_image = tf.gather(images_0_3, [0, 2], axis=3)
print("out_image的shape:", out_image.shape)
可见,输出的通道数变为了2:

(2)tf.gather_nd()
通过 tf.gather_nd,可以通过指定每次采样的坐标来实现采样多个点的目的。考虑班级成绩册的例子,共有 4 个班级,每个班级 35 个学生,8 门科目,保存成绩册的张量 shape 为[4,35,8]。
x = tf.random.uniform([4,35,8],maxval=100,dtype=tf.int32)
现希望抽查第 2 个班级的第 2 个同学的所有科目,第 3 个班级的第 3 个同学的所有科目,第 4 个班级的第 4 个同学的所有科目。那么这 3 个采样点的索引坐标可以记为:[1,1],[2,2],[3,3],我们将这个采样方案合并为一个 List 参数:[[1,1],[2,2],[3,3]],通过tf.gather_nd 实现如下:
y = tf.gather_nd(x,[[1,1],[2,2],[3,3]])
抽查的3个学生的所有8个科目的成绩信息如下:

当然,也可以通过 tf.gather_nd 多维度坐标收集数据。例如抽出班级 1,学生 1 的科目 2;班级 2,学生 2 的科目 3;班级 3,学生 3 的科目 4 的成绩,共有 3 个成绩数据,结果汇总为一个 shape 为[3]的张量:
y1 = tf.gather_nd(x,[[1,1,2],[2,2,3],[3,3,4]])
输出的对应信息如下:

(3)tf.boolean_mask
除了可以通过给定索引号的方式采样,还可以通过给定掩码(mask)的方式采样。继续以 shape 为[4,35,8]的成绩册为例,这次我们以掩码方式进行数据提取。
例如,我们要对第1个班级和第3个班级的数据进行提取,可以设置掩码为:Mask=[True, False, True, False]。然后进行如下操作:
x = tf.random.uniform([4,35,8],maxval=100,dtype=tf.int32)
y2 = tf.boolean_mask(x, mask=[True, False, True, False], axis=0)
print("y2.shape:", y2.shape)
获得提取数据的shape为:

(4)scatter_nd
通过 tf.scatter_nd(indices, updates, shape)可以高效地刷新张量的部分数据,但是只能在全 0 张量的白板上面刷新,因此可能需要结合其他操作来实现现有张量的数据刷新功能。
如下图所示,演示了一维张量白板的刷新运算,白板的形状表示为 shape 参数,需要刷新的数据索引为 indices,新数据为 updates,其中每个需要刷新的数据对应在白板中的位置,根据 indices 给出的索引位置将 updates 中新的数据依次写入白板中,并返回更新后的白板张量。
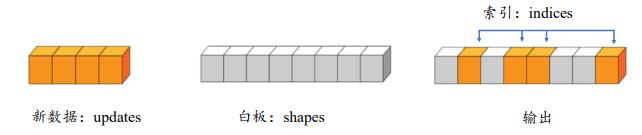
在索引4的位置插入4,在索引3的位置插入5,在索引1的位置插入1,在索引7的位置插入8,实现如下:
# 构造需要刷新数据的位置
indices = tf.constant([[4], [3], [1], [7]])
# 构造需要写入的数据
updates = tf.constant([4, 5, 1, 8])
# 在长度为 8 的全 0 向量上根据 indices 写入 updates
out = tf.scatter_nd(indices, updates, [8])
print("out:", out)
更新后的向量输出out:

(5)meshgrid
通过 tf.meshgrid 可以方便地生成二维网格采样点坐标,方便可视化等应用场合。下面绘制 Sinc 函数在𝑥 ∈ [−8,8], 𝑦 ∈ [−8,8]区间的 3D 曲面。
首先在 x 轴上进行采样 100 个数据点,y 轴上采样 100 个数据点,然后通过tf.meshgrid(x, y)即可返回这 10000 个数据点的张量数据,shape 为[100,100,2]。为了方便计算,tf.meshgrid 会返回在 axis=2 维度切割后的 2 个张量 a,b,其中张量 a 包含了所有点的 x 坐标,b 包含了所有点的 y 坐标,shape 都为[100,100]。
TensorFLow2实现如下:
首先需要导
以上是关于TensorFlow2 入门指南 | 06 TensorFLow2 高阶操作汇总的主要内容,如果未能解决你的问题,请参考以下文章
TensorFlow2 入门指南 | 10 TensorBoard可视化
TensorFlow2 入门指南 | 10 TensorBoard可视化
TensorFlow2 入门指南 | 19 模型文件的保存与加载
TensorFlow2 入门指南 | 19 模型文件的保存与加载