二叉树遍历高级算法之Morris---莫里斯算法

Posted 大忽悠爱忽悠

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二叉树遍历高级算法之Morris---莫里斯算法相关的知识，希望对你有一定的参考价值。

莫里斯算法与线索二叉树有异曲同工之妙，建议先了解线索二叉树，再来学习

Morris算法

莫里斯算法思想

  • mirror遍历用到了线索二叉树的思想,在Morris方法中不需要为每个节点额外分配指针指向其前(predecessor）和后继节点（successor）,只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了 。
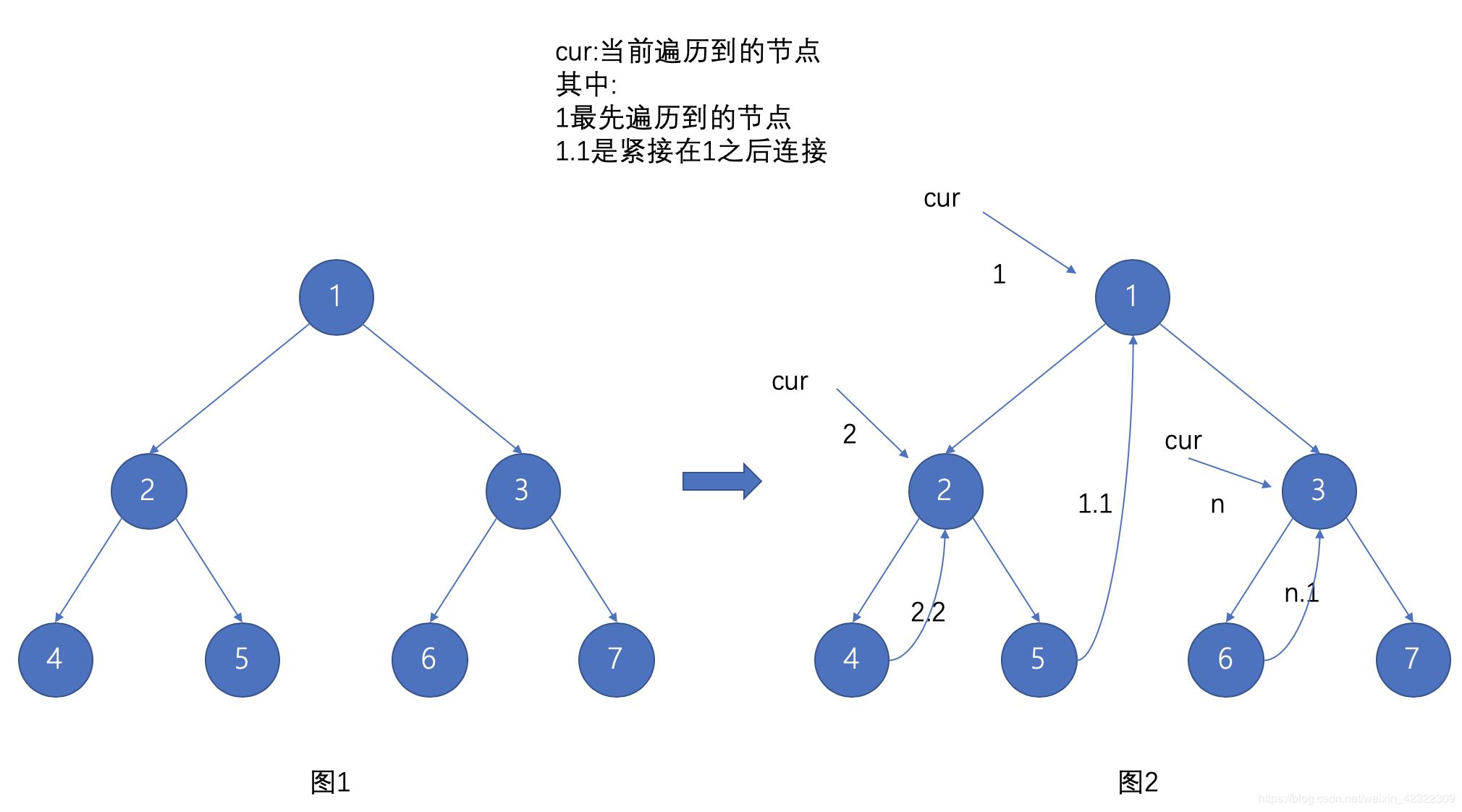
    在这里插入图片描述
    Morris的整体思路就是将 以某个根结点开始，找到它左子树的最右侧节点之后与这个根结点进行连接
    我们可以从 图2 看到，如果这么连接之后，cur 这个指针是可以完整的从一个节点顺着下一个节点遍历，将整棵树遍历完毕，直到 7 这个节点右侧没有指向。
    代码整体模板演示:
  • 如果可以建议大家反复对照上图与代码，和我给出关于自己的详细思考，好好想想。
  • 我尽可能做到对每条代码都做出详细解释
class Solution {
public: 
    void preOrderMorris(TreeNode* root) {
        if (root == NULL)
            return;
        TreeNode* curr = root;  // 当前的结点
        TreeNode* currLeft = NULL;  // 当前结点的左子树
        while (curr != NULL) 
        {
            currLeft = curr->left;
            // 当前结点的左子树存在即可建立连接
            if (currLeft != NULL) 
            {
                // 找到当前左子树的最右侧节点，并且不能沿着连接返回上层
                while (currLeft->right != NULL && currLeft->right != curr)
                    currLeft = currLeft->right;
                //最右侧节点的右指针没有指向根结点，创建连接并往下一个左子树的根结点进行连接操作
                if (currLeft->right == NULL) 
                {
                    currLeft->right = curr;
                    curr = curr.left;
                    continue;  // 这个continue很关键
                } 
                else 
                //当左子树的最右侧节点有指向根结点，此时说明我们已经进入到了返回上层的阶段，不再是一开始的建立连接阶段，同时在回到根结点时我们应已处理完下层节点，直接断开连接即可。
                    currLeft->right = NULL;
            } 
            // 返回上层的阶段不断向右走
            curr = curr.right;
        }
    }
}
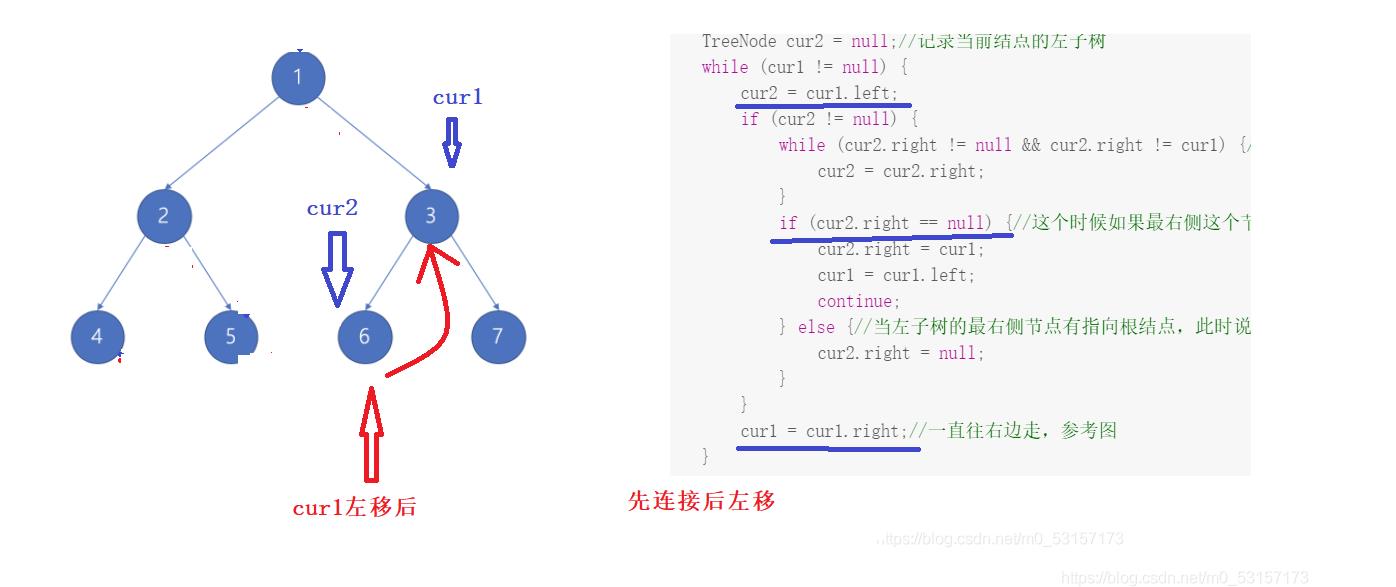
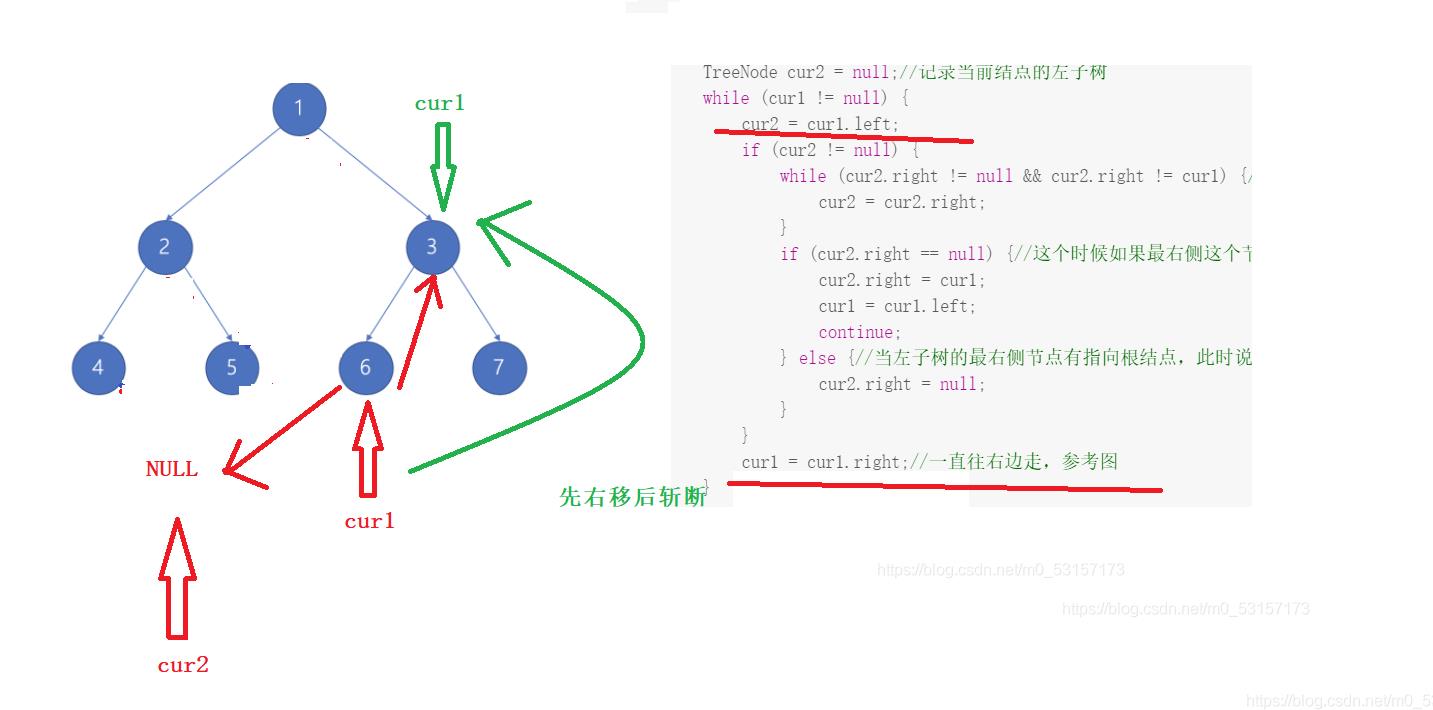
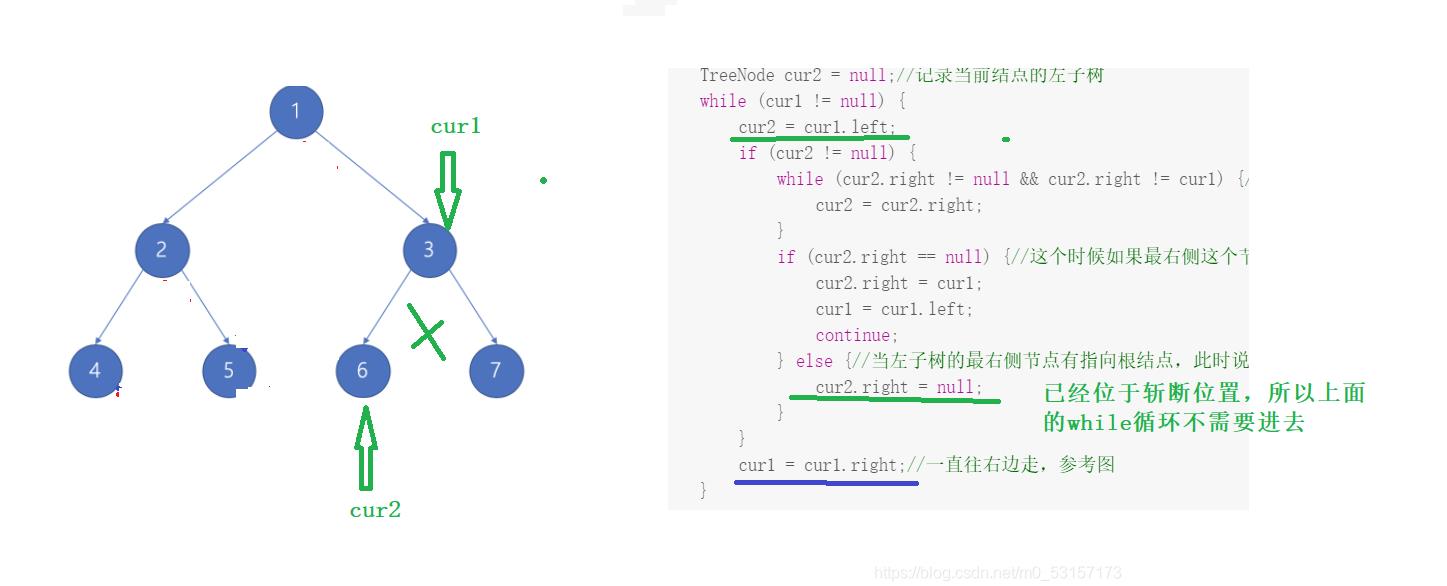
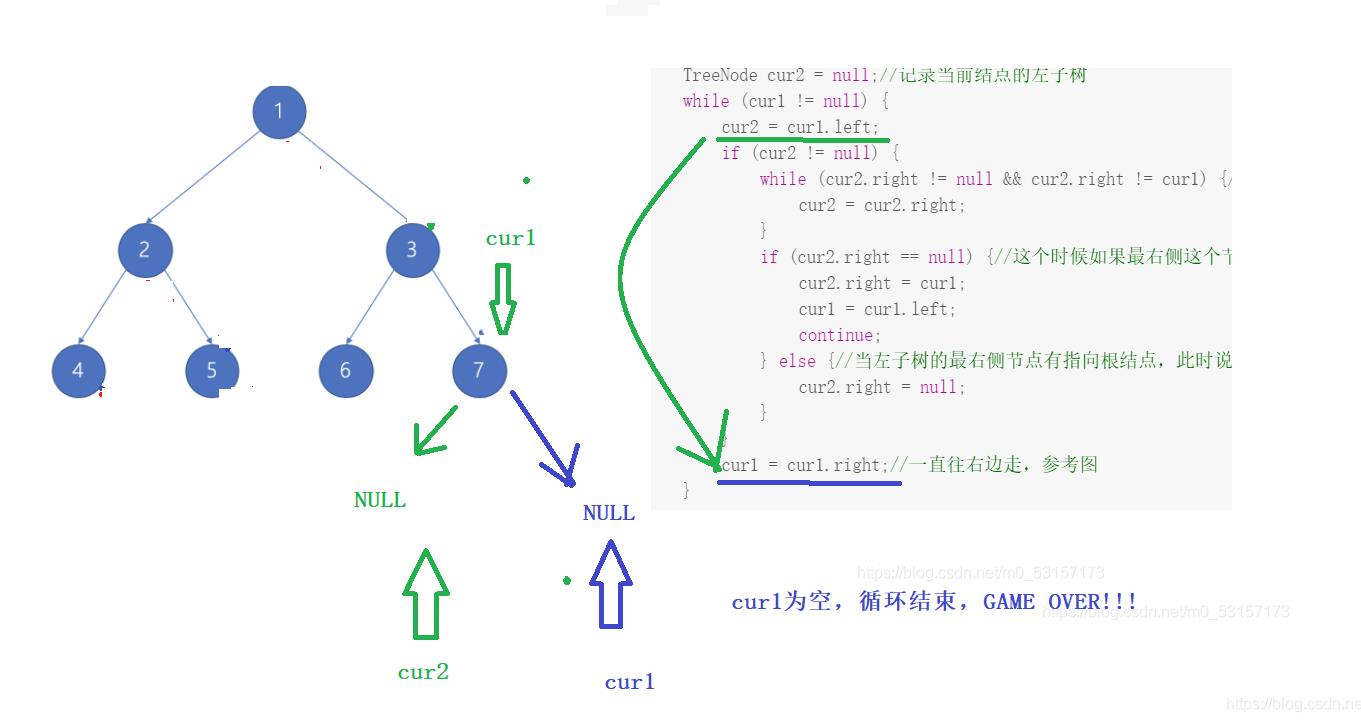
  • 上面的代码和解释可能看完后依旧糊涂，没关系，下面我通过图来演示cur1和cur2指针移动的过程:
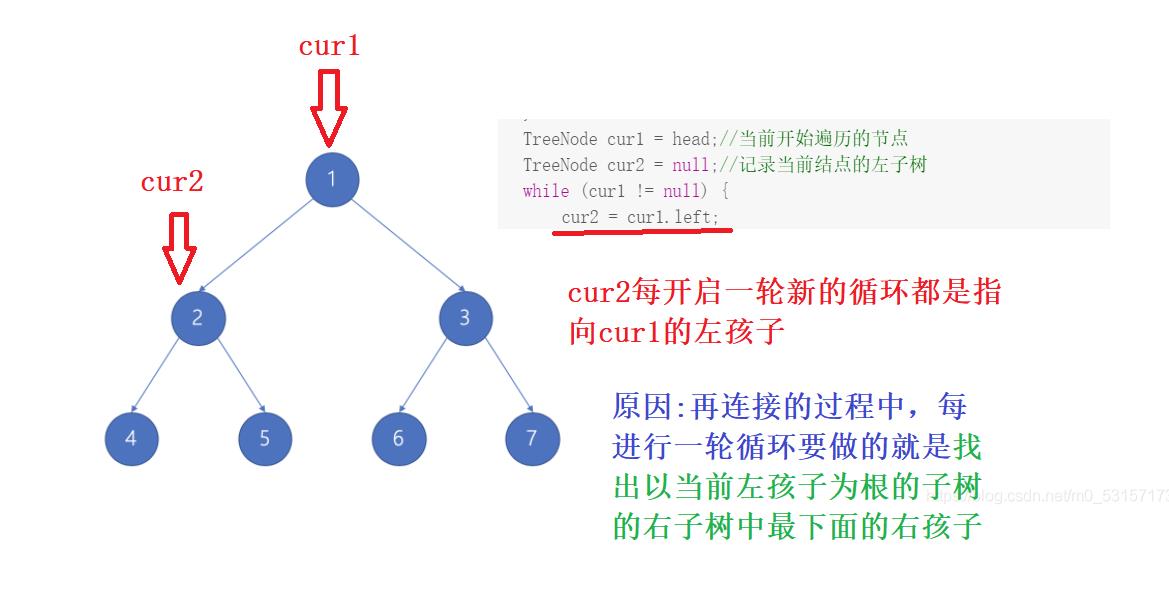
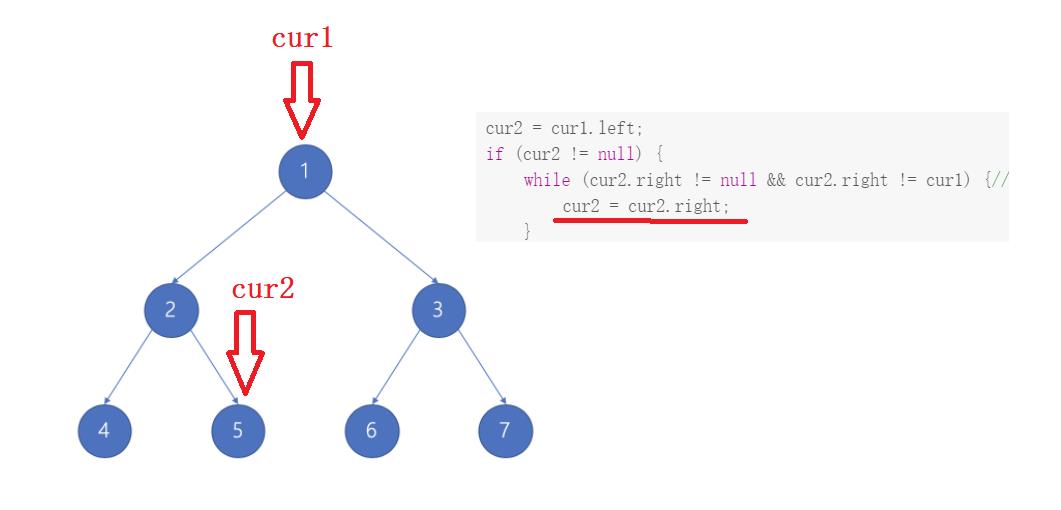
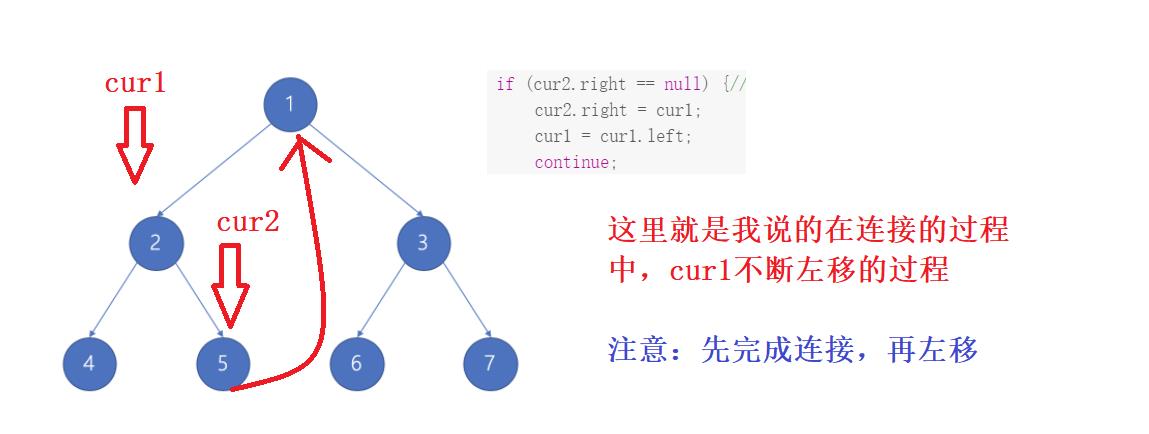
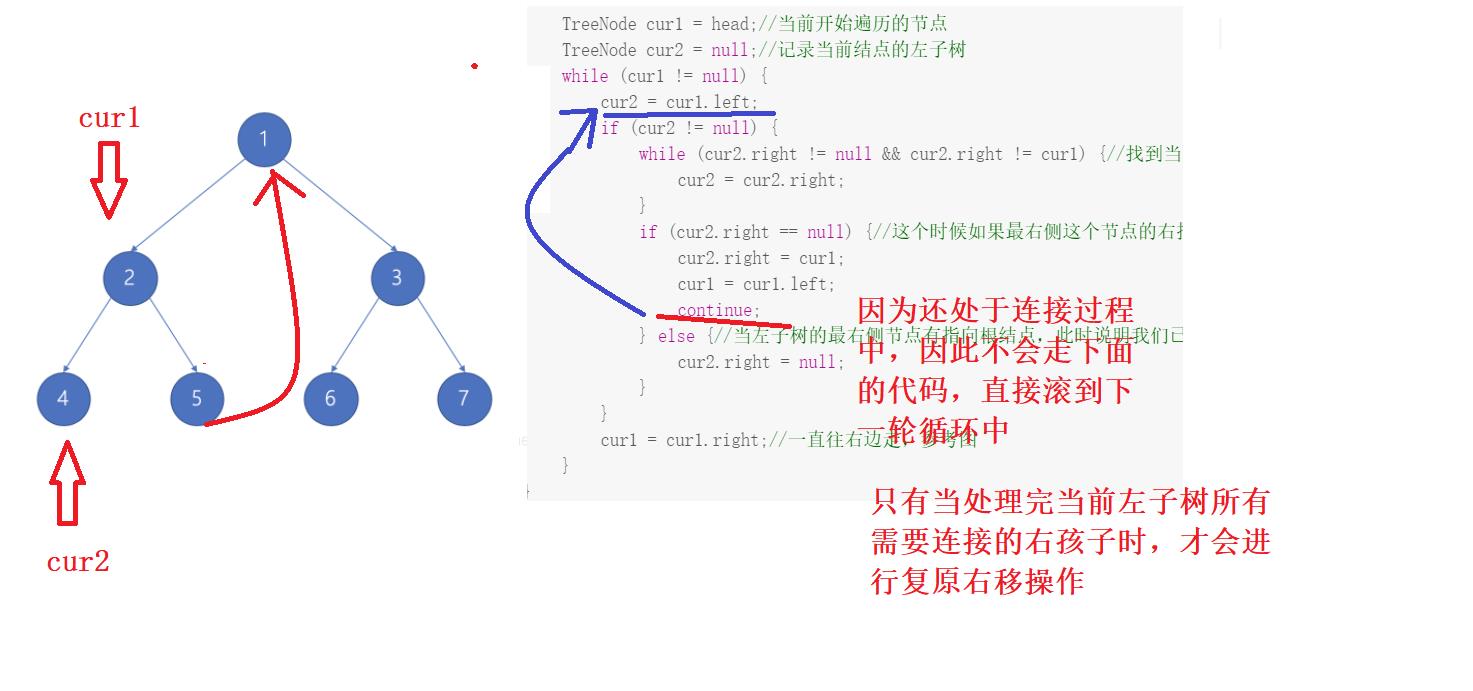
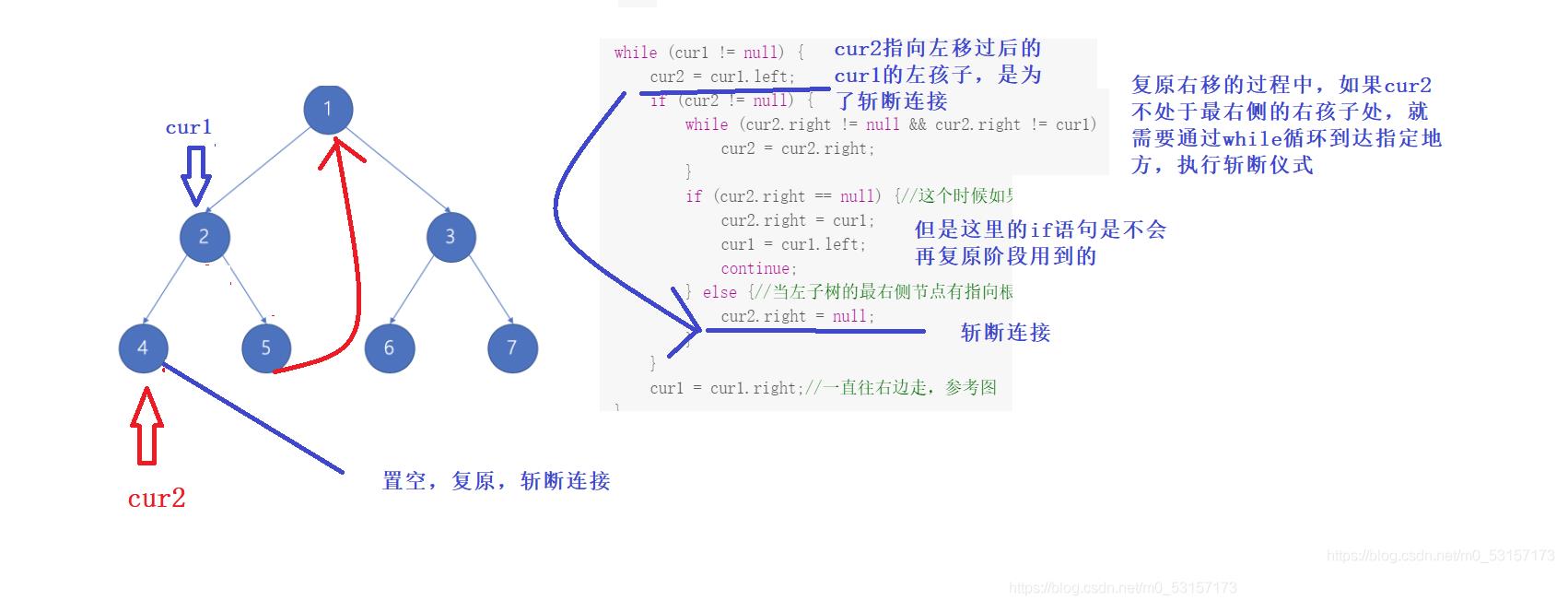
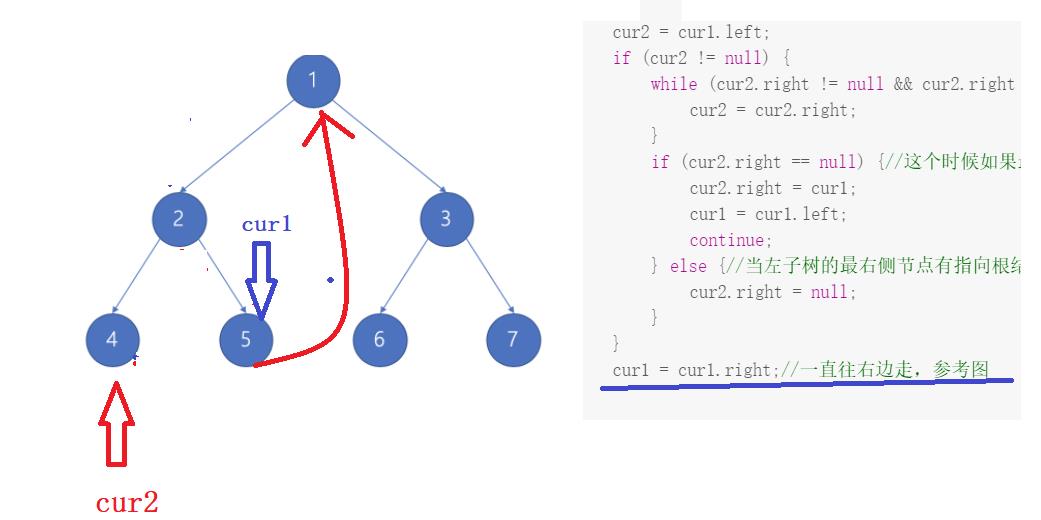
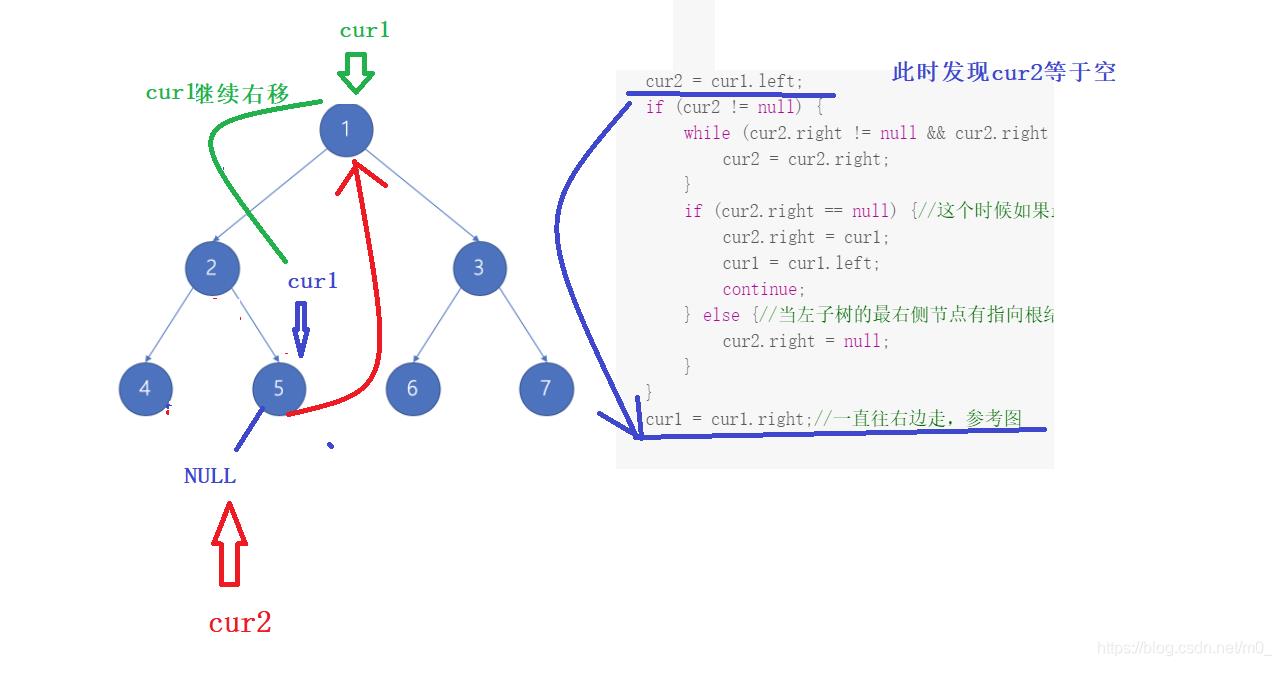
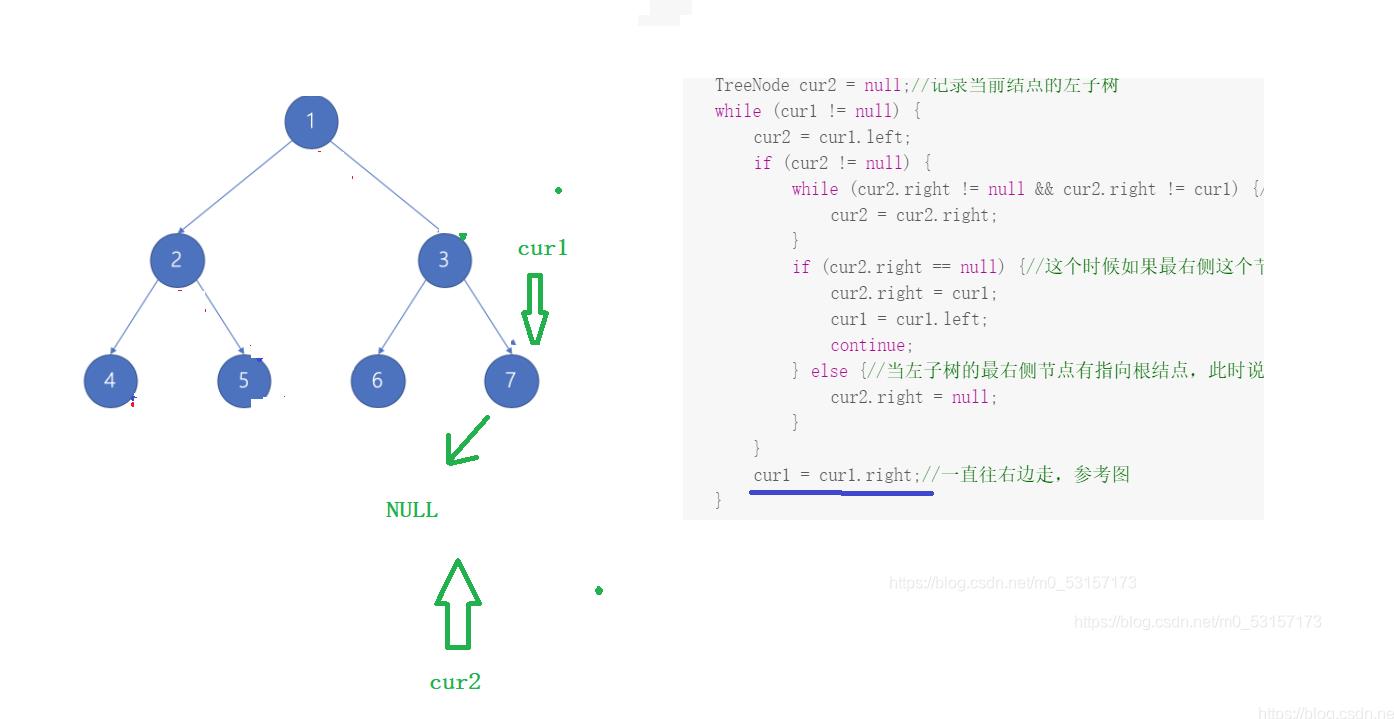
    在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

  • 到此为止，左子树部分就已经处理完毕了，下面右子树

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

总结:

  • 连接过程:先连接后左移
  • 复原过程：先右移后斩断，若斩断位置到位，立刻执行斩断，如果位置不到位，通过while循环到达指定位置

前序遍历

  • Morris建立连接时是给每个根结点寻找其左子树的最右侧结点建立连接，因此“从根结点开始”这一特性很符合前序遍历“中左右”的遍历方式，因此在给结点建立连接的同时输出此根结点即可完成前序遍历。

特殊处理：

  • 建立连接的同时输出此根结点。
  • 到达一些没有子节点的叶子节点，直接输出并向右走返回上层或向此节点的右子树前进。
  • 判断出某节点已有连接，则不用输出，直接断开走过的连接后继续向右走。
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (root == NULL)
            return ans;
        TreeNode* cur1 = root;  // 当前的结点
        TreeNode* cur2 = NULL;  // 当前结点的左子树
        while (cur1 != NULL)
        {
            cur2 = cur1->left;
            // 当前结点的左子树存在即可建立连接
            if (cur2 != NULL)
            {
                // 找到当前左子树的最右侧节点，并且不能沿着连接返回上层
                while (cur2->right != NULL && cur2->right != cur1)
                    cur2 = cur2->right;
                //最右侧节点的右指针没有指向根结点，创建连接并往下一个左子树的根结点进行连接操作
                if (cur2->right == NULL)
                {
                    cur2->right = cur1;
                    ans.push_back(cur1->val);
                    cur1 = cur1->left;
                    continue;  // 这个continue很关键
                }
                else
                    // 当左子树的最右侧节点有指向根结点，此时说明我们已经进入到了返回上层的阶段，不再是一开始的建立连接阶段，同时在回到根结点时我们应已输出过下层节点，直接断开连接即可
                    cur2->right = NULL;
            }
            else
                // 当前节点的左子树为空，说明左侧到头，直接输出
                ans.push_back(cur1->val);
            // 返回上层的阶段不断向右走
            cur1 = cur1->right;
        }
        return ans;
    }
};

在这里插入图片描述

中序遍历

思路：
类似迭代，整个二叉树中输出的第一个节点是最左侧结点，因此在建立连接的时候是不能够直接输出的，必须在建立连接阶段完成，到达最左侧结点之后返回上层的阶段，才能开始输出，此时正好符合“左中右”的遍历方式。
特殊处理：

  • 在建立连接阶段并不输出结点。
  • 在找到最左侧结点（即根结点的左子树为空）时，开始向右走返回上层并同时输出当前结点。
  • 对右子树也进行同样的处理。
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (root == NULL)
            return ans;
        TreeNode* cur1 = root;  // 当前的结点
        TreeNode* cur2 = NULL;  // 当前结点的左子树
        while (cur1 != NULL)
        {
            cur2 = cur1->left;
            // 当前结点的左子树存在即可建立连接
            if (cur2 != NULL)
            {
                // 找到当前左子树的最右侧节点，并且不能沿着连接返回上层
                while (cur2->right != NULL && cur2->right != cur1)
                    cur2 = cur2->right;
                //最右侧节点的右指针没有指向根结点，创建连接并往下一个左子树的根结点进行连接操作
                if (cur2->right == NULL)
                {
                    cur2->right = cur1;
                    cur1 = cur1->left;
                    continue;  // 这个continue很关键
                }
                else
                    // 当左子树的最右侧节点有指向根结点，此时说明我们已经进入到了返回上层的阶段，不再是一开始的建立连接阶段，同时在回到根结点时我们应已输出过下层节点，直接断开连接即可
                    cur2->right = NULL;
            }
                // 当前节点的左子树为空，说明左侧到头，直接输出
                ans.push_back(cur1->val);
            // 返回上层的阶段不断向右走
            cur1 = cur1->right;
        }
        return ans;
    }
};

在这里插入图片描述

后序遍历

思路：
后序遍历又双叒叕是最难搞的情况。举个例子：
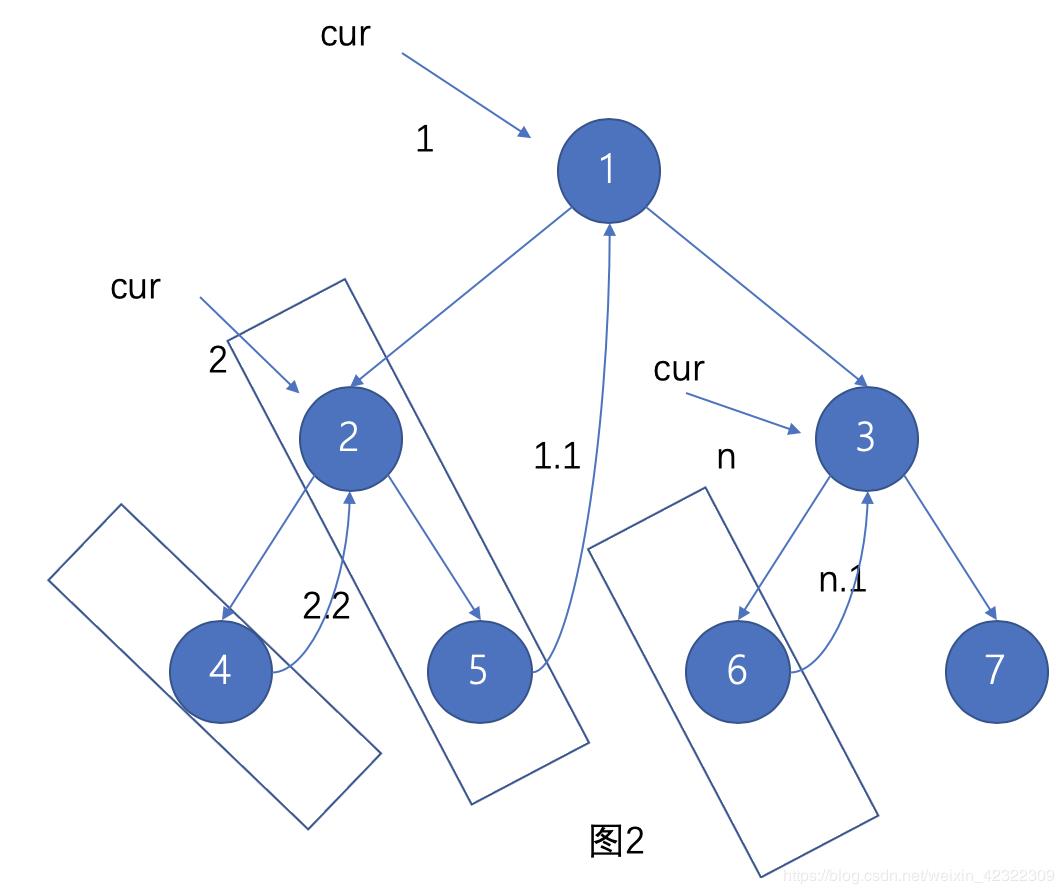
在这里插入图片描述

  • 打印顺序：打印 4 打印 5 2 打印 6 打印 7 3 1
  • 我们将一个节点的连续右节点当成一个单链表来看待，可以发现，输出顺序是将此单链表翻转后输出。
  • 当我们返回上层之后，也就是将连线断开的时候，输出下层的单链表。
  • 比如返回到　２，此时打印　４
  • 比如返回到　１，此时打印　５　２
  • 比如返回到　３，此时打印　６
  • 那么我们只需要将这个单链表逆序输出即可。
  • note：这里不应该打印当前层，而是之前的一层，否则根结点会先与右边输出。
class Solution {
public: 
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (root == NULL)
            return ans;
        TreeNode* curr = root;  // 当前的结点
        TreeNode* currLeft = NULL;  // 当前结点的左子树
        while (curr != NULL) {
            currLeft = curr->left;
            // 当前结点的左子树存在即可建立连接
            if (currLeft != NULL) 
            {
                // 找到当前左子树的最右侧节点，并且不能沿着连接返回上层
                while (currLeft->right != NULL && currLeft->right != curr)
                    currLeft = currLeft->right;
                //最右侧节点的右指针没有指向根结点，创建连接并往下一个左子树的根结点进行连接操作
                if (currLeft->right == NULL) 
                {
                    currLeft->right = curr;
                    curr = curr->left;
                    continue;  // 这个continue很关键
                } 
                // 当左子树的最右侧节点有指向根结点，此时说明我们已经进入到了返回上层的阶段，断开连接同时对之前的一层进行翻转并输出
                else 
                {
                    currLeft->right = NULL;
                    postMorrisPrint(curr->left, ans);
                }
                    
            }
            // 返回上层的阶段不断向右走
            curr = curr->right;
        }
        // 最后一轮循环结束时，从root结点引申的右结点单链表并没有输出，这里补上
        postMorrisPrint(root, ans);
        return ans;
    }
    //输出函数
    void postMorrisPrint(TreeNode* head, vector<int>& ans) {
        TreeNode* newhead = postMorrisReverseList(head);  // newhead为翻转后的新头部
        TreeNode* curr = newhead;
        while (curr != NULL) 
        {
            ans.push_back(curr->val);
            curr = curr->right;
        }
        postMorrisReverseList(newhead);  // 遍历结束后再次翻转恢复原链表
    }
    //翻转单链表函数
    TreeNode* postMorrisReverseList(TreeNode* head) {
        TreeNode* curr = head;
        TreeNode* pre = NULL;  // 哨兵结点
        while (curr != NULL) 
        {
            TreeNode* next = curr->right;
            curr->right = pre;
            pre = curr;
            curr = next;
        }
        return pre;
    }
}

在这里插入图片描述

以上是关于二叉树遍历高级算法之Morris---莫里斯算法的主要内容，如果未能解决你的问题，请参考以下文章

二叉树的Morris遍历算法

二叉树的遍历——Morris

二叉树神级遍历方法

马士兵LeetCode算法讲解

线索二叉树

二叉树遍历之非递归算法