专题数据结构算法笔记之——二叉树的遍历

Posted 2021-05-05 Java进修班

【专题】二叉树的遍历

image-20210501122038438

image-20210501124051938

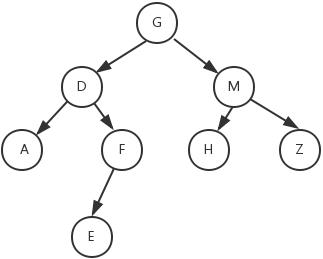
1.DFS(深度优先搜索)——先序遍历

• 访问顺序：先根节点，然后左子树，最后右子树。上图访问结果为：GDAFEMHZ

• 递归实现：

1public void preOrderTraverse1(TreeNode root) {
2        if (root != null) {
3
4            System.out.print(root.val + "->");
5
6            preOrderTraverse1(root.left);
7            preOrderTraverse1(root.right);
8        }
9    }

 

• 非递归实现：

 1public void preOrderTraverse2(TreeNode root) {
 2        Stack<TreeNode> stack = new Stack<>();
 3        TreeNode node = root;
 4        while (node != null || !stack.empty()) {
 5            if (node != null) {
 6
 7                System.out.print(node.val + "->");
 8
 9                stack.push(node);
10                node = node.left;
11            } else {
12                TreeNode tem = stack.pop();
13                node = tem.right;
14            }
15        }
16    }

2.DFS(深度优先搜索)——中序遍历

• 访问顺序：先左子树，再根节点，最后右子树。上图访问结果为：ADEFGHMZ

• 递归实现：

1public void inOrderTraverse(TreeNode root) {
2        if (root != null) {
3            inOrderTraverse(root.left);
4
5            System.out.print(root.val + "->");
6
7            inOrderTraverse(root.right);
8        }
9    }

 

• 非递归实现：

 1public void inOrderTraverse(TreeNode root) {
 2        Stack<TreeNode> stack = new Stack<>();
 3        TreeNode node = root;
 4        while (node != null || !stack.isEmpty()) {
 5            if (node != null) {
 6                stack.push(node);
 7                node = node.left;
 8            } else {
 9                TreeNode tem = stack.pop();
10
11                System.out.print(tem.val + "->");
12
13                node = tem.right;
14            }
15        }
16    }

 

【例题】

二叉搜索树的第k大节点

【题目】

给定一棵二叉搜索树，请找出其中第k大的节点

---

【示例1】

1输入：root = [3,1,4,null,2],k = 1
2输出：4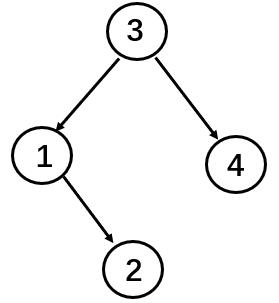

   

image-20210428210049301

【示例2】

1输入：root = [5,3,6,2,4,null,null,1], k = 3
2输出：4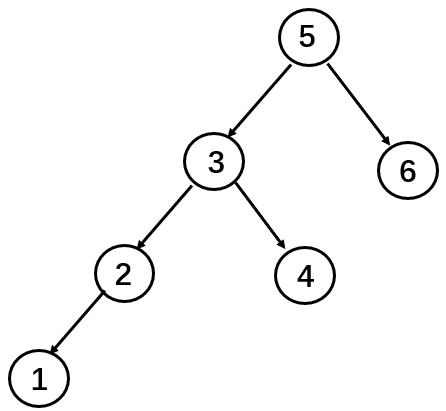

   

image-20210428210507226

---

【思路】

• 看到二叉搜索树，马上想到二叉搜索树的特性：

【搜索树概念】根节点左边都比根节点小，右边都比根节点大，递归满足，所有节点都是如此的。

• 所以马上想到二叉搜索树的中序遍历方法，中序遍历方法可以天然的将二叉搜索树按序排列。或从小到大或从大到小这样排列，排列后再在其内部进行一个具体操作即可。

• 中序遍历（按从小到大进行排序）：

 1    /**
 2     * 中序遍历（从小到大）：先左 +再中 +后右
 3     */
 4
 5    List<Node> list = new ArrayList<>();
 6    public void traversal(Node node){
 7        if (node != null){
 8            traversal(node.left);
 9
10            //这是具体的处理逻辑
11            list.add(node);
12
13            traversal(node.right);
14        }
15    }

   

• 中序遍历（按从大到小进行排序）：

 1    /**
 2     * 中序遍历（从大到小）：先右 +再中 +后左
 3     */
 4
 5    List<Node> list = new ArrayList<>();
 6    public void traversal(Node node){
 7        if (node != null){
 8            traversal(node.right);
 9
10            //这是具体的处理逻辑
11            list.add(node);
12
13            traversal(node.left); 
14        }
15    }

   

• 于本题而言，首先按照中序遍历法，将二叉搜索树进行排序，只要排好序，取其第k大的数就好办了

---

【代码及分析】

方法一、中序遍历按从小到大的顺序排，再取其倒数第k位即可：

 1package ceshi;
 2import java.util.ArrayList;
 3import java.util.List;
 4
 5class Codec {
 6    public int kthLargest(TreeNode root, int k) {
 7        //调取递归方法
 8        traversal(root);
 9        //返回要求的倒数第k位值
10        return list.get(list.size()-k);
11    }
12
13    //定义ArrayList用来存放各节点值
14    List<Integer> list = new ArrayList<>();
15    private void traversal(TreeNode root) {
16        //中序遍历（从小到大）
17        if (root != null){
18            traversal(root.left);
19
20            list.add(root.val);
21
22            traversal(root.right);
23        }
24    }
25
26
27    public class TreeNode {
28      int val;
29      TreeNode left;
30      TreeNode right;
31      TreeNode(int x) { val = x; }
32    }
33}

   

方法二、中序遍历按从大到小的顺序排，再取其正数第k位即可：

 1package ceshi;
 2import java.util.ArrayList;
 3import java.util.List;
 4
 5class Codec {
 6    public int kthLargest(TreeNode root, int k) {
 7        //调取递归方法
 8        traversal(root);
 9        //返回要求的正数第k位值
10        return list.get(k - 1);
11    }
12
13    //定义ArrayList用来存放各节点值
14    List<Integer> list = new ArrayList<>();
15    //中序遍历（从大到小）
16    private void traversal(TreeNode root) {
17        if (root != null){
18            traversal(root.right);
19
20            list.add(root.val);
21
22            traversal(root.left);
23        }
24    }
25
26
27    public class TreeNode {
28      int val;
29      TreeNode left;
30      TreeNode right;
31      TreeNode(int x) { val = x; }
32    }
33}

   

---

【复杂度分析】

• 时间：O(N)，当树退化为链表时（即全部为右子节点），递归深度为N，占用O(N)时间

• 空间：O(N)，当树退化为链表时（即全部为右子节点），系统使用O(N)大小的栈空间。

3.DFS(深度优先搜索)——后序遍历

• 访问顺序：先左子树，再右子树，最后根节点，上图的访问结果为：AEFDHZMG。

• 递归实现：

1public void postOrderTraverse(TreeNode root) {
2        if (root != null) {
3            postOrderTraverse(root.left);
4            postOrderTraverse(root.right);
5
6            System.out.print(root.val + "->");
7
8        }
9    }

 

• 非递归实现：

 1public void postOrderTraverse(TreeNode root) {
 2        TreeNode cur, pre = null;
 3
 4        Stack<TreeNode> stack = new Stack<>();
 5        stack.push(root);
 6
 7        while (!stack.empty()) {
 8            cur = stack.peek();
 9            if ((cur.left == null && cur.right == null) || (pre != null && (pre == cur.left || pre == cur.right))) {
10                System.out.print(cur.val + "->");
11                stack.pop();
12                pre = cur;
13            } else {
14                if (cur.right != null)
15                    stack.push(cur.right);
16                if (cur.left != null)
17                    stack.push(cur.left);
18            }
19        }
20    }

 

---

【例题】

二叉树的深度

【题目】

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

---

【示例】

给定二叉树[3,9,20,null,null,15,7],返回它的最大深度为3

image-20210428221407016

---

【思路】

• 关键点：二叉树的深度和其左（右）子树的深度之间的关系。显然，树的深度等于子左树的深度与右子树的深度中的最大值再加1；

• 终止条件：当root为空，说明已越过叶节点，因此返回深度为0；

• 递归体：计算节点root的左子树深度，调用maxDepth(root.left)；

• 递归体：计算节点root的左子树深度，调用maxDepth(root.right)；

---

【代码及分析】

 1package ceshi;
 2
 3class Codec {
 4    public int maxDepth(TreeNode root) {
 5        //若空，返0
 6        if (root == null)  return 0;
 7
 8        //非空，返回遍历左右两叉的最大值+1
 9        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
10    }
11
12
13
14
15    class TreeNode {
16        int val;
17        TreeNode left;
18        TreeNode right;
19        TreeNode(int x) {
20            val = x;
21        }
22    }
23}

   

---

【复杂度分析】

• 时间：O(N)，N为树的节点数量，计算树的深度需要遍历树的全部节点

• 空间：O(N)，最差情况下，树退化为链表，递归深度可达到N

4.BFS（广度优先搜索）——层序遍历

• 访问顺序：一层一层来访问。上图访问结果为：GDMAFHZE

• 实现：

 1public void levelOrderTraverse(TreeNode root) {
 2        if (root == null) {
 3            return;
 4        }
 5        Queue<TreeNode> queue = new LinkedList<TreeNode>();
 6        queue.add(root);
 7
 8        while (!queue.isEmpty()) {
 9            TreeNode node = queue.poll();
10
11            System.out.print(node.val + "->");
12
13            if (node.left != null) {
14                queue.add(node.left);
15            }
16            if (node.right != null) {
17                queue.add(node.right);
18            }
19        }
20    }

 

【例题】

从上到下打印二叉树Ⅰ

【题目】

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

---

【示例】

给定二叉树：[3,9,20,null,null,15,7]

image-20210420213200167

返回：[3,9,20,15,7]

---

【思路】本题难以想到的是将二叉树的节点存放入一个队列queue中

• 首先，定义一个队列，将二叉树的所有节点放入，后面用到时候一一拿出来

• 定义一个ArrayList用来临时存放数值，到后面再将这个ArrayList转到数组中进行返回输出

• 首先考虑，假如该二叉树是空的，直接返回即可。如果不空：

• 进入循环体，因为不知道循环次数，故使用while循环。只要从队列queue不为空，就进入循环体

• 在循环体中，将queue中存放的节点poll出来，拿出来后将其值加入到ArrayList当中

• 然后依次往下看，看该节点的左叉树如果不为空，将左叉树放入queue中，同理，该节点的右叉树如果不为空，将右叉树放入queue中。

• 直到为空，跳出循环，ArrayList中放满了数字，将数字转存到int型数组中返回即可！

---

【代码及分析】

 1package ceshi;
 2import java.util.ArrayList;
 3import java.util.LinkedList;
 4import java.util.Queue;
 5
 6class Solution {
 7    public int[] levelOrder(TreeNode root) {
 8        //我试过了ArrayList来放，时间超限，故还是用队列queue来存放
 9        //将二叉树的所有节点都存放在一个队列queue中
10        Queue<TreeNode> queue = new LinkedList<>(){{ add(root); }};
11
12        //因为树的大小不定，故新定义ArrayList来存放终值
13        ArrayList<Integer> array = new ArrayList<>();
14
15        if (root == null)  return new int[0];
16
17        //只要队列不为空，就一直取值
18        while (!queue.isEmpty()){
19            TreeNode node = queue.poll();
20
21            //拿出节点将其值放入ArrayList中
22            array.add(node.val);
23
24            if (node.left != null) {
25                queue.add(node.left);
26            }
27
28            if (node.right != null){
29                queue.add(node.right);
30            }
31        }
32
33        //将ArrayList中的值一一赋值到数组中进行返回
34        int[] arr = new int[array.size()];
35        for (int i = 0; i < array.size() ; i++) {
36            arr[i] = array.get(i);
37        }
38        return arr;
39    }
40
41
42    public class TreeNode {
43      int val;
44      TreeNode left;
45      TreeNode right;
46      TreeNode(int x) { val = x; }
47    }
48}

   

---

【复杂度分析】

• 时间：O(N)，N 为二叉树的节点数量，需循环 N 次。

• 空间：O(N)，最差情况下。二叉树演变为链表，最多有 N/2个树节点放入queue中，这样占用了O(N)的额外空间。