树二叉树完全/满/平衡二叉树的理解与对比

Posted 2021-05-05 网络技术干货圈

优质文章，及时送达

今天给大家带来的是数据结构中的树，包括是二叉树、完全/满/平衡二叉树，大家可以看下目录：

• 一、树

• 1.1、相关概念

• 1.2、定义

• 1.3、特点

• 1.4、表示方法

• 1.5、示例图

• 二、二叉树

• 2.1、定义

• 2.2、基本形态

• 2.3、示例图

• 三、完全二叉树

• 3.1、定义

• 3.2、示例图

• 四、满二叉树

• 4.1、定义

• 4.2、特点

• 4.3、示例图

• 五、平衡二叉树（AVL树）

• 5.1、特点

• 5.2、平衡因子

• 5.3、示例图

• 5.4、失衡调整

• 六、数据对比

一、树

树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很像自然界中的树那样。树型结构也是信息的重要组织形式之一，一切具有层次关系的问题都可用树来描述。

1.1、相关概念

• 路径：顺着节点的边从一个节点走到另一个节点，所经过的节点的顺序排列就称为路径；
• 根：树顶端的节点称为根，一棵树只有一个根，如果要把一个节点和边的集合称为树，那么从根到其他任何一个节点都必须有且只有一条路径；
• 父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 兄弟节点：具有相同父节点的节点互称为兄弟节点；
• 叶节点：没有子节点的节点称为叶节点，也叫叶子节点；
• 子树：每个节点都可以作为子树的根，它和它所有的子节点、子节点的子节点等都包含在子树中；
• 节点的层次：从根开始定义，根为第一层，根的子节点为第二层，以此类推；
• 深度：对于任意节点n，n的深度为从根到n的唯一路径长，根的深度为0；
• 高度：对于任意节点n，n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0；
• 森林：0个或多个不相交的树组成，对森林加上一个根，森林即成为树；删去根，树即成为森林；
• 节点的度：节点拥有的子树的数目；
• 树的度：树中节点的最大的度；
• 叶子节点：度为零的节点；
• 分支节点：度不为零的节点；
• 层次：根节点的层次为1，其余节点的层次等于该节点的双亲节点的层次加1；
• 树的高度：树中节点的最大层次；
• 无序树：树中节点的各子树之间的次序是不重要的，可以交换位置；
• 有序树：树中节点的各子树之间的次序是重要的，不可以交换位置；

1.2、定义

• 树是由一个或多个节点组成的有限集合；
• 树中必有一个特定的称为根的节点；
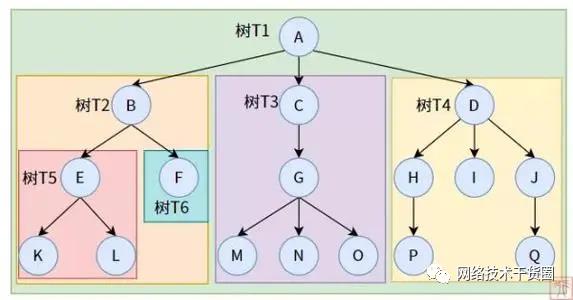
• 剩下的节点被分成 n>=0 个互不相交的集合T1、T2、…Tn，并且这些每个集合又都是一个树。树T1、T2、…Tn被称作根的子树；

1.3、特点

• 对比二叉树
• 树中节点的最大度数（节点的分叉）没有限制，而二叉树节点的最大度数（节点的分叉）数量为2；
• 树的节点无左、右之分，而二叉树的节点有左、右之分；

1.4、表示方法

树的表示方法有许多，常用的方法是用括号：

• 先将根结点放入一对圆括号中，然后把它的子树由左至右的顺序放入括号中，而对子树也采用同样的方法处理；
• 同层子树与它的根节点用圆括号括起来，同层子树之间用逗号隔开，最后用闭括号括起来；

1.5、示例图

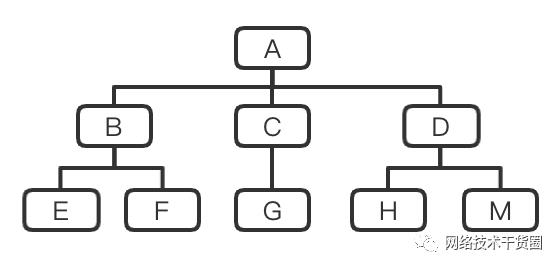
树

如上图可使用括号表示法写成：(A(B(E,F),C(G),D(H,M)))

二、二叉树

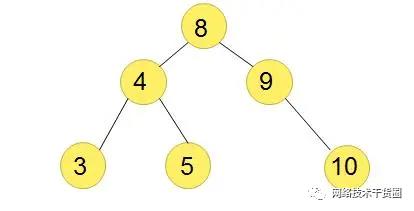
二叉树（Binary Tree）是包含n个节点的有限集合，当n为零时该集合为空集，或者该集合由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。

2.1、定义

• 树中每个节点最多有两个子树，不存在度（分叉）大于2的节点；
• 子树有左右之分，次序不能颠倒；

2.2、基本形态

• 空二叉树
• 只有一个根结点的二叉树
• 只有右子树
• 只有左子树
• 完全二叉树：除了树的最后一层外，其他的节点既有左子树又有右子树；

2.3、示例图

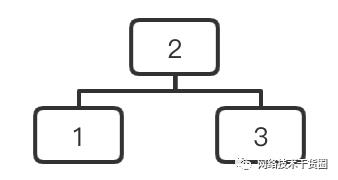
二叉树

三、完全二叉树

对于深度为 k ，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 k的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

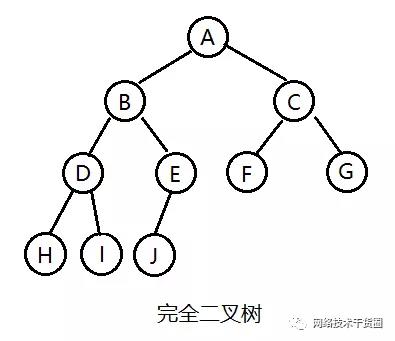
3.1、定义

• 符合二叉树的定义规则；
• 除二叉树的最高层h外，其它各层 (1～h-1) 的节点数都达到最大个数；
• 第h层有叶子结点，并且叶子结点都是从左到右依次排布；

3.2、示例图

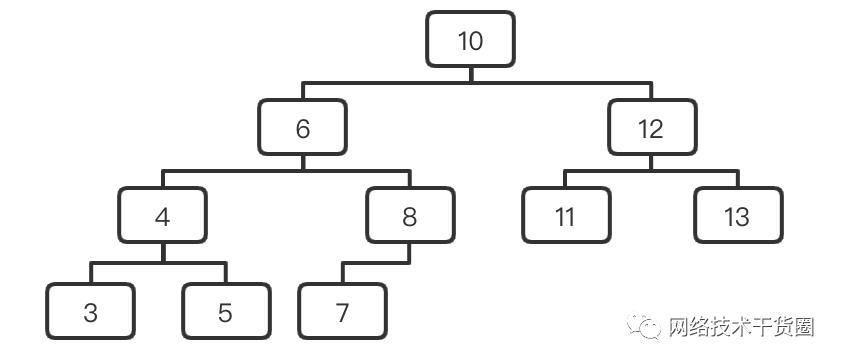
完全二叉树

四、满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为 k，且结点总数是 2^k−1 ，则它就是满二叉树。

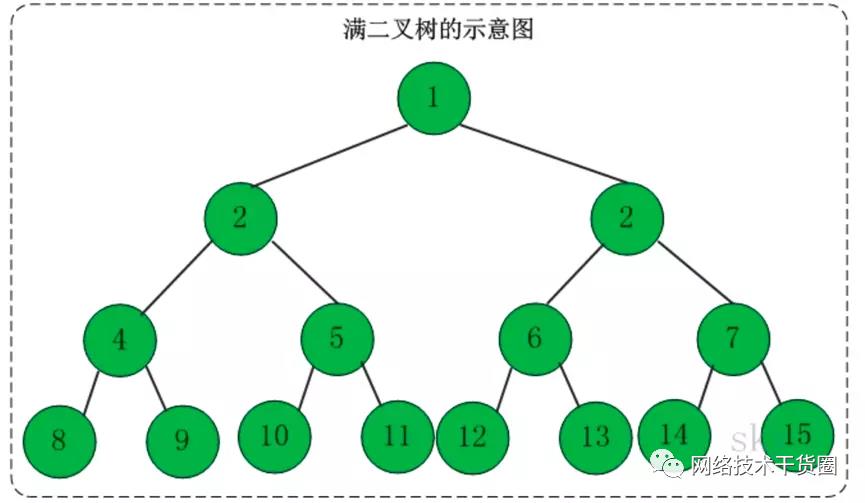
4.1、定义

• 符合完全二叉树的定义；
• 每个节点都有左右子叶并且叶子节点都处于最底层；

4.2、特点

满二叉树一定是平衡二叉树，平衡二叉树不一定是满二叉树；

4.3、示例图

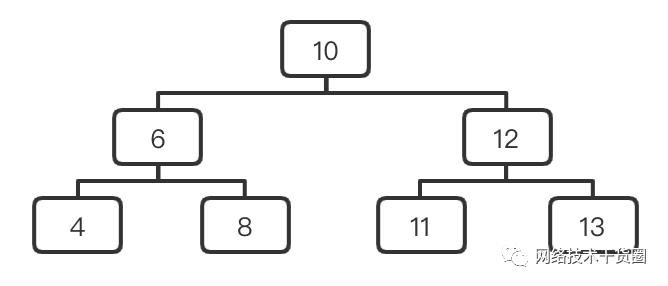
满二叉树

五、平衡二叉树（AVL树）

平衡二叉树（又称平衡二叉查找树），由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962年提出的高度平衡的二叉树，根据科学家的英文名也称为 AVL树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。

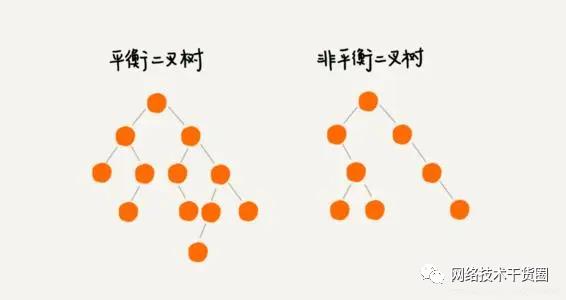
最小二叉平衡树的节点的公式为F(n)=F(n-1)+F(n-2)+1，这个类似于一个递归的数列，可参考Fibonacci数列，公式解释为：

• 1是根节点；
• F(n-1)是左子树的节点数量；
• F(n-2)是右子树的节点数量；

5.1、特点

• 可以为空树；
• 左右子树的高度相差不超过 1 （平衡因子的绝对值不超过1）的树，并且左右子数都是一个平衡二叉树；

5.2、平衡因子

• 1：表示左子树比右子树高；
• 0：表示右子树比左子树高；
• 1：表示左子树和右子树等高；

5.3、示例图

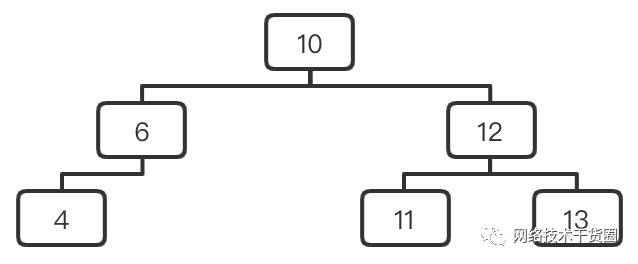
平衡二叉树

5.4、失衡调整

平衡二叉树调整后，它的中序遍历的顺序是不会改变的。

5.4.1、插入时的失衡调整

所有的不平衡情况中，都是按照寻找最小不平衡树 => 寻找所属的不平衡类别 => 根据4种类别进行固定化程序的操作；

5.4.1.1、LL型调整（左子树过高）

首先找到最小不平衡的子树，再以其根节点向右旋转（向右旋转后相当于右面的子数的树高加1，而左面的子数的树高减1）；旋转之后源根节点的左孩子作为新的根节点，原来根节点的左孩子作为新的根节点；中序遍历对比：调整前：123；调整后：123；LL型调整 LL型调整

5.4.1.2、RR型调整（右子树过高）

• 首先找到最小不平衡的子树，再以其根节点向左旋转（向右旋转后相当于左面的子数的树高加1，而右面的子数的树高减1）；
• 旋转之后源根节点的右孩子作为新的根节点，原来根节点的右孩子作为新的根节点；
• 中序遍历对比：调整前：123；调整后：123；

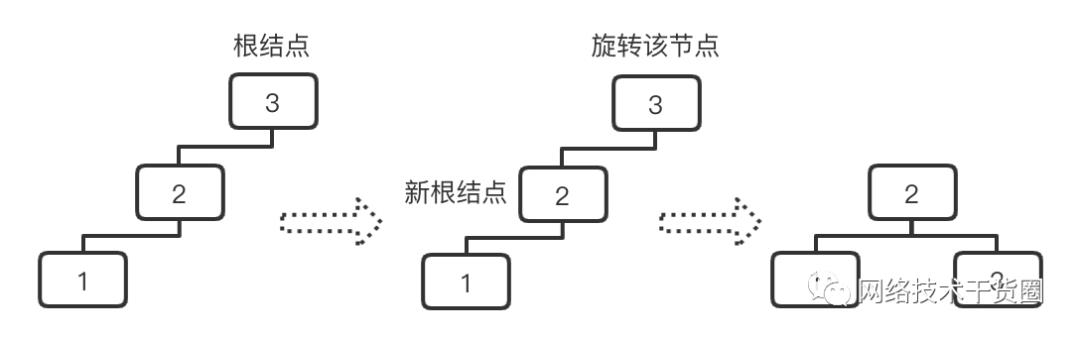
RR型调整

5.4.1.3、LR型调整（左子树过高）

• 以较高子树的根节点为中心向左进行旋转（示例图中为左子树较高，左子树的根为节点1），可以理解成先转换为LL型；

• 以原根节点为中心，向右旋转（实例图中以节点3为中心，向右旋转）；

• 调整之后，原来根节点的左孩子的右孩子作为新的根节点；

• 中序遍历对比：调整前：123；调整后：123；

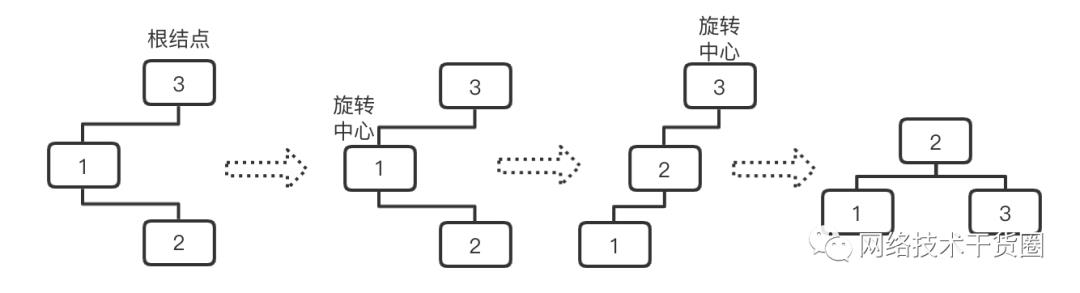
LR调整

5.4.1.4、RL型调整（右子树过高）

• 以根节点的右孩子为中心向右进行旋转（示例图中为右子树较高，右子树的根为节点3），可以理解成先转换为RR型；

• 以原根节点为中心，向右旋转（示例图中以节点1为中心，向左旋转）；

• 调整之后，原来根节点的右孩子的左孩子作为新的根节点；

• 中序遍历对比：调整前：123；调整后：123；

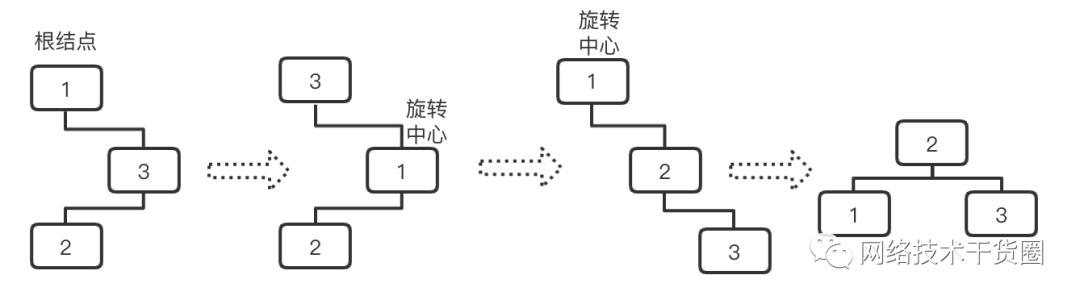
RL调整

5.4.2、删除时的失衡调整

5.4.2.1、LE型（左子树过高）

以下初始场景只会在删除时才会出现，删除后可按照LL型的调整策略进行调整；

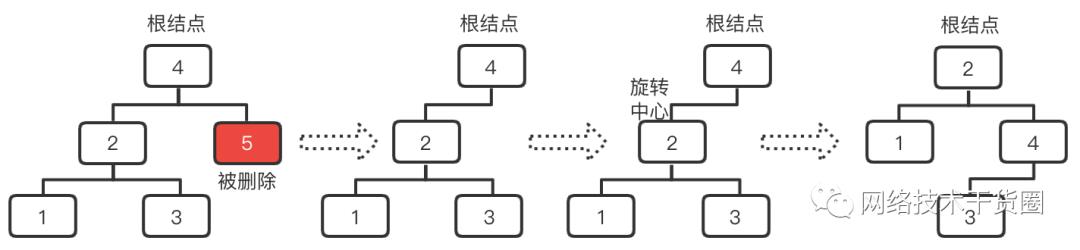
LE调整

5.4.2.2、RE型（右子树过高）

以下初始场景只会在删除时才会出现，删除后可按照RR型的调整策略进行调整；

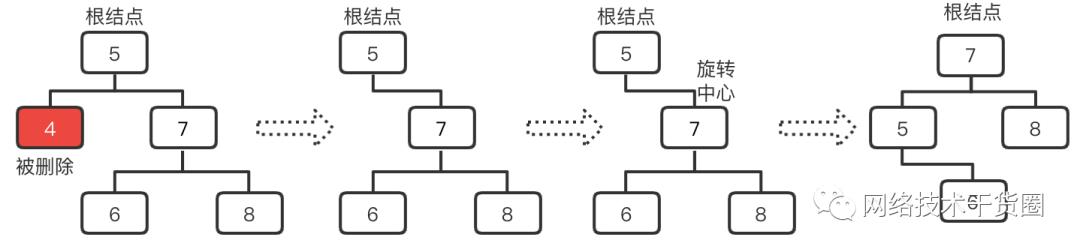
RE调整

六、数据对比

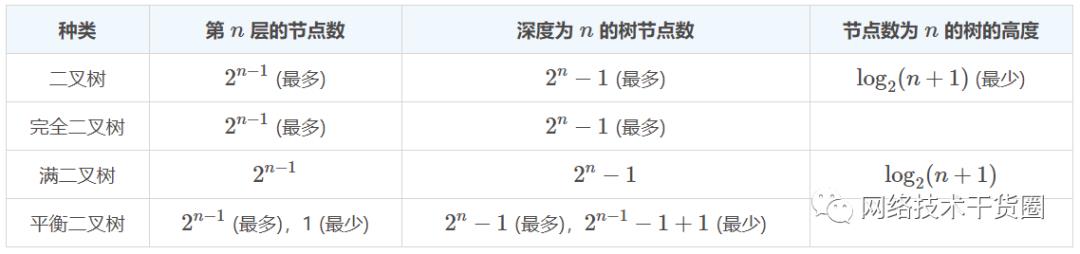
---END---

重磅！网络技术干货圈-技术交流群已成立

扫码可添加小编微信，申请进 群。

一定要备注： 工种+地点+学校/公司+昵称（如网络工程师+南京+苏宁+猪八戒） ，根据格式备注，可更快被通过且邀请进群

▲长按加群

以上是关于树二叉树完全/满/平衡二叉树的理解与对比的主要内容，如果未能解决你的问题，请参考以下文章

算法漫游指北（第十三篇）:二叉树的基本概念满二叉树完全二叉树二叉树性质二叉搜索树二叉树定义二叉树的广度优先遍历

二叉树及特殊二叉树（满二叉树完全二叉树二叉排序树平衡二叉树）的定义和性质（附详细推理过程）

树二叉树满二叉树完全二叉树遍历二叉树java实现

数据结构树相关代码（数据结构笔试复测Leecode牛客）

二叉树详解

面试---算法面试