四平衡二叉树/AVL树

Posted 2021-05-05 星星之陨

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了四平衡二叉树/AVL树相关的知识，希望对你有一定的参考价值。

4.1、基本定义

（1）平衡二叉树

平衡二叉树（balance binary tree)又称为AVL树（根据它的发明者G.M. Adelson-Velsky和E.M. Landis命名的），或者是一棵空的二叉排序树，或者是具有下列性质的二叉排序树：

（1）根节点的左子树和右子树的深度最多相差1

（2）根节点的左子树和右子树也都是平衡二叉树

（2）平衡因子

节点的平衡因子（balance factor）是该节点的左子树的深度与右子树的深度之差

（3）最小不平衡树

最小不平衡树（minimal unbalance subtree）是指在平衡二叉树的构造过程中，以距离插入节点最近的、且平衡因子的绝对值大于1的节点为根节点的树。

4.2、构造思想

在构造二叉排序树的过程中，每当插入一个节点时，首先检查是否因为插入而破坏了树的平衡性。若是，则找出最小不平衡树。在保持二叉排序的前提下，调整最小不平衡树中各个节点之前的链接关系，进行相应的旋转，使之成为新的平衡子树。

4.3、旋转

4.3.1、失衡状态

失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)、(右左)

4.3.1.1、LL：LeftLeft（"左左"）

插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。

例如：由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

4.3.1.2、LR：LeftRight（"左右"）

插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。

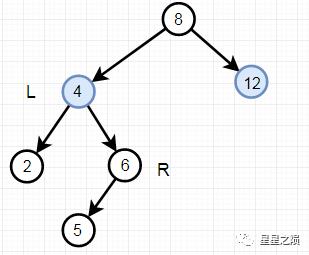
例如：由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

4.3.1.3、RL：RightLeft（"右左"）

插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

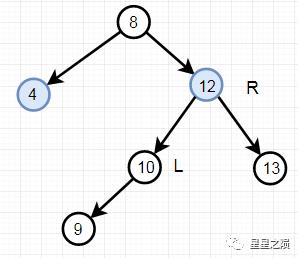
例如：由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

4.3.1.4、RR：RightRight（"右右"）

插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

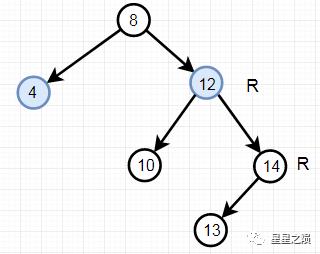
例如：由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

4.3.2、旋转失衡

如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。AVL失去平衡之后，可以通过旋转使其恢复平衡，下面分别介绍"LL(左左)，LR(左右)，RR(右右)和RL(右左)"这4种情况对应的旋转方法。

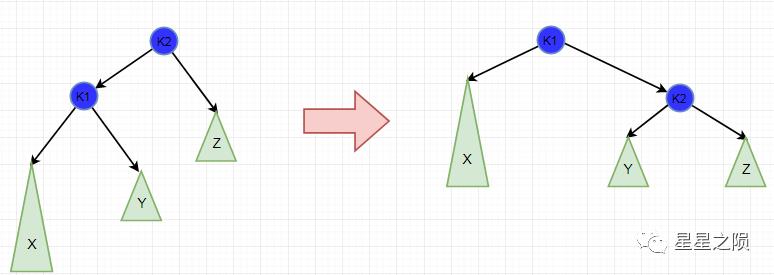
4.3.2.1、LL旋转

LL旋转是围绕"失去平衡的AVL根节点"进行的，也就是节点k2

用手抓着"左孩子，即k1"使劲摇。将k1变成根节点，k2变成k1的右子树，"k1的右子树"变成"k2的左子树"。

示例：

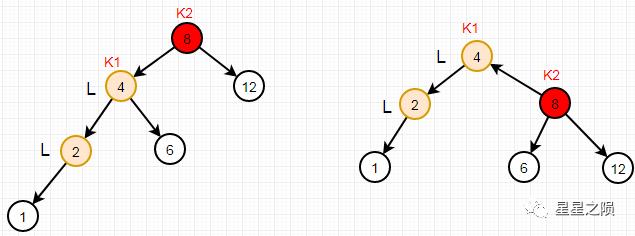
失去平衡的节点为根节点k2，它左子树k1高度为3，右子树高度为1，相差2

对根节点K2，进行LL旋转：

k2的左子树变为k1的右子树

k1的右子树变为k2

原根节点的左子树k1（即第一个L)，变为根节点

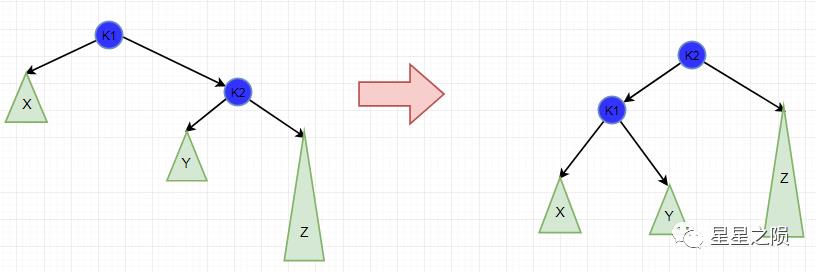
4.3.2.2、RR旋转

RR是与LL对称的情况

用手抓着"右孩子，即k2"使劲摇。将k2变成根节点，k1变成k2的左子树，"k2的左子树"变成"k1的右子树"。

示例

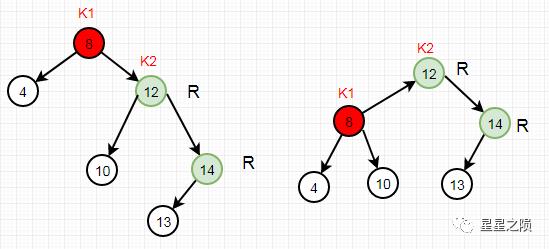
失去平衡的节点为根节点K1，它右子树k2高度为3，左子树高度为1，相差2

对根节点K1，进行RR旋转：

k1的右子树变为k2的左子树

k2的左子树变为k1

原根节点的右子树k2（即第一个R)，变为根节点

4.3.2.3、LR旋转

需要经过两次旋转

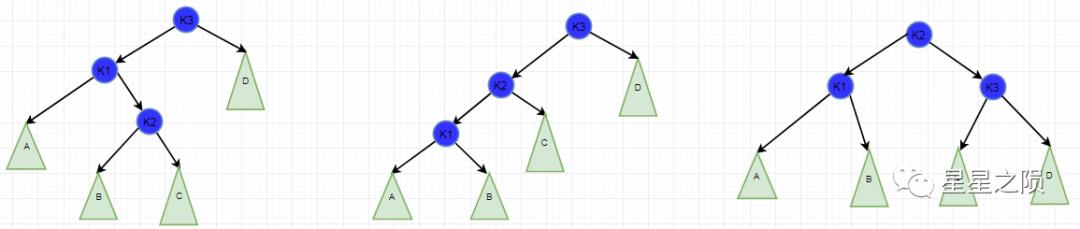
第一次：围绕K1，即LR中的L，进行RR旋转

第二次：围绕K2，即LR中的R，进行LL旋转

示例：

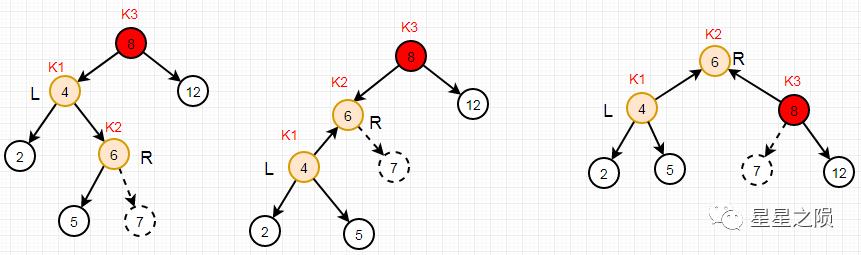
第一步：针对根节点的左节点K1，进行RR旋转

此时将K1看为独立的树，k1为根节点，重复上述RR旋转过程

RR旋转后得到中间图

第二步：针对RR后的根节点K3，进行LL旋转

此时K1，K2，K3为独立的树，K3为根节点，重复上述LL旋转过程

LL旋转后得到最终树

虚线节点7与节点5不会同时出现

4.3.2.4、RL旋转

需要经过两次旋转

第一次：围绕K3，即RL中的R，进行LL旋转

第二次：围绕K2，即RL中的L，进行RR旋转

示例：

第一次：针对根节点的右节点K3，进行LL旋转

此时将K3看为独立的树，k3为根节点，重复上述LL旋转过程

LL旋转后得到中间图

第二次：针对LL后的根节点K1，进行RR旋转

此时K1，K2，K3为独立的树，K1为根节点，重复上述RR旋转过程

RR旋转后得到最终树

虚线节点11与节点9不会同时出现

4.3.3、旋转代码

 /**
  * LL旋转
  * 
  * @param k2
  *            k2节点
  * @return 旋转后的根节点
  */
 private TreeNode<T> leftLeftRotation(TreeNode<T> k2) {
  TreeNode<T> k1;
        //初始化K1节点
  k1 = k2.left;

  k2.left = k1.right;
  k1.right = k2;
  k2.height = max(height(k2.left), height(k2.right)) + 1;
  k1.height = max(height(k1.left), k2.height) + 1;
  return k1;
 }

 /**
  * RR旋转
  * 
  * @param k1
  *            k1节点
  * @return 旋转后的根节点
  */
 private TreeNode<T> rightRightRotation(TreeNode<T> k1) {
  TreeNode<T> k2;
        //初始化K2节点
  k2 = k1.right;

  k1.right = k2.left;
  k2.left = k1;
  k1.height = max(height(k1.left), height(k1.right)) + 1;
  k2.height = max(height(k2.right), k1.height) + 1;
  return k2;
 }

 /**
  * LR旋转
  * 
  * @param k3
  *            k3旋转
  * @return 旋转后的根节点
  */
 private TreeNode<T> leftRightRotation(TreeNode<T> k3) {
  // 第一步：RR旋转
  k3.left = rightRightRotation(k3.left);
  // 第二步：LL旋转
  return leftLeftRotation(k3);
 }

 /**
  * RL旋转
  * 
  * @param k1
  *            k1节点
  * @return 旋转后的根节点
  */
 private TreeNode<T> rightLeftRotation(TreeNode<T> k1) {
  // 第一步：LL旋转
  k1.right = leftLeftRotation(k1.right);
  // 第二步：RR旋转
  return rightRightRotation(k1);
 }

4.4、插入节点

4.4.1、基本思想

每次新创建节点，需要设置该节点的高度height（新创建的节点高度都为1）
每次在节点的左子树或右子树插入节点，都要对该节点进行重新设置高度
设置完节点高度，判断节点的左右子树是否平衡，不平衡则进行旋转

如果插入数据大于该节点的右子树数据，则是RR旋转（此时是插到该节点的右子树的右子树RR）
如果插入数据小于该节点的右子树数据，则是RL旋转（此时是插到该节点的右子树的左子树RL）
如果插入数据小于该节点的左子树数据，则是LL旋转（此时是插到该节点的左子树的左子树LL）
如果插入数据大于该节点的左子树数据，则是LR旋转（此时是插到该节点的左子树的右子树LR）
如果插入的节点在该节点的左子树，则进行LL旋转或者LR旋转
如果插入的节点在该节点的右子树，则进行RR旋转或者RL旋转
对该节点旋转后需要重新赋值到该节点

最后将该节点赋值到根节点，实现递归调用

4.4.2、示例代码

 /**
  * 插入节点
  * 
  * @param key
  *            插入数据
  */
 public void insert(T key) {
  this.root = insertNode(this.root, key);
 }

 /**
  * 插入
  * 
  * @param node
  *            节点
  * @param data
  *            数据
  * @return 插入后的节点
  */
 private TreeNode<T> insertNode(TreeNode<T> node, T data) {
  if (node == null) {
   node = new TreeNode<>(data);
   node.height = max(height(node.left), height(node.right)) + 1;
   return node;
  }
  // 插入到node的左子树
  if (node.data.compareTo(data) > 0) {
   node.left = insertNode(node.left, data);
   // 重新设置node的高度
   node.height = max(height(node.left), height(node.right)) + 1;
   // 判断是否平衡
   if (height(node.left) - height(node.right) == 2) {
    if (data.compareTo(node.left.data) < 0)
     node = leftLeftRotation(node);
    else
     node = leftRightRotation(node);
   }
  }
  // 插入到node的右子树
  else if (node.data.compareTo(data) < 0) {
   node.right = insertNode(node.right, data);
   // 重新设置node的高度
   node.height = max(height(node.left), height(node.right)) + 1;
   // 判断是否平衡
   if (height(node.right) - height(node.left) == 2) {
    if (data.compareTo(node.right.data) > 0)
     node = rightRightRotation(node);
    else
     node = rightLeftRotation(node);
   }
  }
  return node;
 }
 /**
  * 节点的高度
  * 
  * @param node
  *            节点
  * @return 高度
  */
 private int height(TreeNode<T> node) {
  if (node != null) {
   return node.height;
  }
  return 0;
 }

4.5、删除节点

4.5.1、基本思想

对于要删除的节点，首先进行查找，是否存在此节点，如果能查找到，则进行删除草，否则不进行删除操作
递归遍历AVL树，查找到要删除的节点

如果左子树高于右子树
如果右子树高于左子树，或者两个相等，则：
最后赋值结果递归返回到要删除的节点。
(01)找出node的左子树中的最大节点
(02)将该最大节点的值赋值给node
(03)删除该最大节点
(01)找出node的右子树中的最小节点
(02)将该最小节点的值赋值给node
(03)删除该最小节点
将不为空的子树赋值给该节点，或者直接赋值该节点为空。
赋值结果递归返回到要删除的节点
如果要删除的节点只有左子树或者只有右子树或者左右子树都为空，则：
如果要删除的节点左右子树都不为空，则：

删除完成后要重新设置node的高度，并且判断是否平衡

如果node.left.right的高度大于node.left.left的高度，则进行LR旋转。

此时node为k3，node.left为k1，node.left.right为k2
如果node.left.right的高度不大于node.left.left的高度，则进行LL旋转

此时node为k2，node.left为k1
如果node.right.left高度大于node.right.right高度，则进行RL旋转。

此时node为k1，node.right为k3，node.right.left为k2
如果node.right.left高度不大于node.right.right高度，则进行RR旋转

此时node为k1，node.right为k2
如果删除的节点是node的左子树中的节点（判断node的右子树高度比左子树是否高2）：
如果删除的节点是node的右子树中的节点（判断node的左子树高度比右子树是否高2）：

4.5.2、示例代码

/**
  * 删除节点
  * 
  * @param data
  */
 public void deleteNode(T data) {
  if (searchTree(data) != null) {
   this.root = deleteNode(this.root, data);
  }
 }

 private TreeNode<T> deleteNode(TreeNode<T> node, T data) {
  if (node == null || node.data == null || data == null) {
   return node;
  }
  if (node.data.compareTo(data) > 0) {
   node.left = deleteNode(node.left, data);
   // 重新设置node的高度
   node.height = max(height(node.left), height(node.right)) + 1;
   // 判断是否平衡
   if (height(node.right) - height(node.left) == 2) {
    TreeNode<T> temp = node.right;
    if (height(temp.left) > height(temp.right)) {
     node = rightLeftRotation(node);
    } else {
     node = rightRightRotation(node);
    }
   }
  } else if (node.data.compareTo(data) < 0) {
   node.right = deleteNode(node.right, data);
   // 重新设置node的高度
   node.height = max(height(node.left), height(node.right)) + 1;
   // 判断是否平衡
   if (height(node.left) - height(node.right) == 2) {
    TreeNode<T> temp = node.left;
    if (height(temp.right) > height(temp.left)) {
     node = leftRightRotation(node);
    } else {
     node = leftLeftRotation(node);
    }
   }
  } else {
   // 左右子树都不为空
   if (node.left != null && node.right != null) {
    // node左子树高于右子树
    if (height(node.left) > height(node.right)) {
     // (01)找出node的左子树中的最大节点
     // (02)将该最大节点的值赋值给node
     // (03)删除该最大节点
     TreeNode<T> max = node.left;
     while (max.right != null) {
      max = max.right;
     }
     node.left = deleteNode(node.left, max.data);
     node.data = max.data;
    }
    // node的左子树不比右子树高(即它们相等，或右子树比左子树高1)
    else {
     // (01)找出node的右子树中的最小节点
     // (02)将该最小节点的值赋值给node
     // (03)删除该最小节点
     TreeNode<T> min = node.right;
     while (min.left != null) {
      min = min.left;
     }
     node.right = deleteNode(node.right, min.data);
     node.data = min.data;
    }
   } else {
    node = node.left != null ? node.left : node.right;
   }
  }
  return node;
 }

4.6、Java代码实现

4.6.1、BalanceBinaryTree

package com.starfall.tree;

import java.util.LinkedList;
import java.util.Queue;

public class BalanceBinaryTree<T extends Comparable<T>> {

 private TreeNode<T> root;

 /**
  * 节点的高度
  * 
  * @param node
  *            节点
  * @return 高度
  */
 private int height(TreeNode<T> node) {
  if (node != null) {
   return node.height;
  }
  return 0;
 }

 /**
  * 获取两数最大值
  * 
  * @param a
  *            数值1
  * @param b
  *            数值2
  * @return 最大值
  */
 private int max(int a, int b) {
  return a > b ? a : b;
 }

 /**
  * LL旋转
  * 
  * @param k2
  *            k2节点
  * @return 旋转后的根节点
  */
 private TreeNode<T> leftLeftRotation(TreeNode<T> k2) {
  TreeNode<T> k1;
  // 初始化K2节点
  k1 = k2.left;

  k2.left = k1.right;
  k1.right = k2;
  k2.height = max(height(k2.left), height(k2.right)) + 1;
  k1.height = max(height(k1.left), k2.height) + 1;
  return k1;
 }

 /**
  * RR旋转
  * 
  * @param k1
  *            k1节点
  * @return 旋转后的根节点
  */
 private TreeNode<T> rightRightRotation(TreeNode<T> k1) {
  TreeNode<T> k2;
  // 初始化K2节点
  k2 = k1.right;

  k1.right = k2.left;
  k2.left = k1;
  k1.height = max(height(k1.left), height(k1.right)) + 1;
  k2.height = max(height(k2.right), k1.height) + 1;
  return k2;
 }

 /**
  * LR旋转
  * 
  * @param k3
  *            k3旋转
  * @return 旋转后的根节点
  */
 private TreeNode<T> leftRightRotation(TreeNode<T> k3) {
  // 第一步：RR旋转
  k3.left = rightRightRotation(k3.left);
  // 第二步：LL旋转
  return leftLeftRotation(k3);
 }

 /**
  * RL旋转
  * 
  * @param k1
  *            k1节点
  * @return 旋转后的根节点
  */
 private TreeNode<T> rightLeftRotation(TreeNode<T> k1) {
  // 第一步：LL旋转
  k1.right = leftLeftRotation(k1.right);
  // 第二步：RR旋转
  return rightRightRotation(k1);
 }

 /**
  * 插入节点
  * 
  * @param key
  *            插入数据
  */
 public void insert(T key) {
  this.root = insertNode(this.root, key);
 }

 /**
  * 插入
  * 
  * @param node
  *            节点
  * @param data
  *            数据
  * @return 插入后的节点
  */
 private TreeNode<T> insertNode(TreeNode<T> node, T data) {
  if (node == null) {
   node = new TreeNode<>(data);
   node.height = max(height(node.left), height(node.right)) + 1;
   return node;
  }
  // 插入到node的左子树
  if (node.data.compareTo(data) > 0) {
   node.left = insertNode(node.left, data);
   // 重新设置node的高度
   node.height = max(height(node.left), height(node.right)) + 1;
   // 判断是否平衡
   if (height(node.left) - height(node.right) == 2) {
    if (data.compareTo(node.left.data) < 0)
     node = leftLeftRotation(node);
    else
     node = leftRightRotation(node);
   }
  }
  // 插入到node的右子树
  else if (node.data.compareTo(data) < 0) {
   node.right = insertNode(node.right, data);
   // 重新设置node的高度
   node.height = max(height(node.left), height(node.right)) + 1;
   // 判断是否平衡
   if (height(node.right) - height(node.left) == 2) {
    if (data.compareTo(node.right.data) > 0)
     node = rightRightRotation(node);
    else
     node = rightLeftRotation(node);
   }
  }
  return node;
 }

 /**
  * 搜索节点数据
  * 
  * @param data
  *            节点数据
  * @return 节点
  */
 public TreeNode<T> searchTree(T data) {
  return searchTree(this.root, data);
 }

 private TreeNode<T> searchTree(TreeNode<T> node, T data) {
  if (node == null || node.data == null || data == null) {
   // 条件不符，未找到相同节点，递归结束
   return null;
  } else if (node.data.compareTo(data) > 0) {
   // 递归遍历左子树
   return searchTree(node.left, data);
  } else if (node.data.compareTo(data) < 0) {
   // 递归遍历右子树
   return searchTree(node.right, data);
  } else {
   // 遍历到相同节点，递归结束
   return node;
  }
 }

 /**
  * 删除节点
  * 
  * @param data
  */
 public void deleteNode(T data) {
  if (searchTree(data) != null) {
   this.root = deleteNode(this.root, data);
  }
 }

 private TreeNode<T> deleteNode(TreeNode<T> node, T data) {
  if (node == null || node.data == null || data == null) {
   return node;
  }
  if (node.data.compareTo(data) > 0) {
   node.left = deleteNode(node.left, data);
   // 重新设置node的高度
   node.height = max(height(node.left), height(node.right)) + 1;
   // 判断是否平衡
   if (height(node.right) - height(node.left) == 2) {
    TreeNode<T> temp = node.right;
    if (height(temp.left) > height(temp.right)) {
     node = rightLeftRotation(node);
    } else {
     node = rightRightRotation(node);
    }
   }
  } else if (node.data.compareTo(data) < 0) {
   node.right = deleteNode(node.right, data);
   // 重新设置node的高度
   node.height = max(height(node.left), height(node.right)) + 1;
   // 判断是否平衡
   if (height(node.left) - height(node.right) == 2) {
    TreeNode<T> temp = node.left;
    if (height(temp.right) > height(temp.left)) {
     node = leftRightRotation(node);
    } else {
     node = leftLeftRotation(node);
    }
   }
  } else {
   // 左右子树都不为空
   if (node.left != null && node.right != null) {
    // node左子树高于右子树
    if (height(node.left) > height(node.right)) {
     // (01)找出node的左子树中的最大节点
     // (02)将该最大节点的值赋值给node
     // (03)删除该最大节点
     TreeNode<T> max = node.left;
     while (max.right != null) {
      max = max.right;
     }
     node.left = deleteNode(node.left, max.data);
     node.data = max.data;
    }
    // node的左子树不比右子树高(即它们相等，或右子树比左子树高1)
    else {
     // (01)找出node的右子树中的最小节点
     // (02)将该最小节点的值赋值给node
     // (03)删除该最小节点
     TreeNode<T> min = node.right;
     while (min.left != null) {
      min = min.left;
     }
     node.right = deleteNode(node.right, min.data);
     node.data = min.data;
    }
   } else {
    node = node.left != null ? node.left : node.right;
   }
  }
  return node;
 }

 /**
  * 前序遍历
  */
 public void preOrder() {
  System.out.print("前序遍历： [  ");
  preOrder(this.root);
  System.out.println("]");
 }

 private void preOrder(TreeNode<T> node) {
  if (node == null) {
   return;
  }
  System.out.print(node.data + "  ");
  preOrder(node.left);
  preOrder(node.right);
 }

 /**
  * 中序遍历
  */
 public void midOrder() {
  System.out.print("中序遍历： [  ");
  midOrder(this.root);
  System.out.println("]");
 }

 private void midOrder(TreeNode<T> node) {
  if (node == null) {
   return;
  }
  midOrder(node.left);
  System.out.print(node.data + "  ");
  midOrder(node.right);
 }

 /**
  * 后序遍历
  */
 public void backOrder() {
  System.out.print("后序遍历： [  ");
  backOrder(this.root);
  System.out.println("]");
 }

 private void backOrder(TreeNode<T> node) {
  if (node == null) {
   return;
  }
  backOrder(node.left);
  backOrder(node.right);
  System.out.print(node.data + "  ");
 }

 /**
  * 层序遍历二叉树
  */
 public void levelOrder() {
  System.out.print("层序遍历： [  ");
  levelOrder(this.root);
  System.out.println("]");
 }

 private void levelOrder(TreeNode<T> node) {
  Queue<TreeNode<T>> q = new LinkedList<>();
  q.offer(node);
  while (!q.isEmpty()) {
   TreeNode<T> temp = q.poll();
   if (temp == null) {
    return;
   }
   System.out.print(temp.data + "  ");
   if (temp.left != null) {
    q.offer(temp.left);
   }
   if (temp.right != null) {
    q.offer(temp.right);
   }
  }
 }

 static class TreeNode<T> {
  private T data;
  private int height;
  private TreeNode<T> left;
  private TreeNode<T> right;

  TreeNode() {

  }

  TreeNode(T data) {
   this.data = data;
  }

  public T getData() {
   return data;
  }

  public void setData(T data) {
   this.data = data;
  }

  public int getHeight() {
   return height;
  }

  public void setHeight(int height) {
   this.height = height;
  }

  public TreeNode<T> getLeft() {
   return left;
  }

  public void setLeft(TreeNode<T> left) {
   this.left = left;
  }

  public TreeNode<T> getRight() {
   return right;
  }

  public void setRight(TreeNode<T> right) {
   this.right = right;
  }
 }
}

4.6.2、BalanceBinaryTreeTest

package com.starfall.tree;

import org.junit.Test;

public class BalanceBinaryTreeTest {
 @Test
 public void test01() {
  BalanceBinaryTree<Integer> bbt = new BalanceBinaryTree<Integer>();
  // int arr[] = { 3, 2, 1, 4, 5, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8, 9 };
  int arr[] = { 1, 2, 3, 4, 5, 6 };
  for (int i = 0; i < arr.length; i++) {
   bbt.insert(arr[i]);
  }
  bbt.preOrder();
  bbt.midOrder();
  bbt.backOrder();
  bbt.levelOrder();
 }

 @Test
 public void test02() {
  BalanceBinaryTree<Integer> bbt = new BalanceBinaryTree<Integer>();
  int arr[] = { 8, 4, 12, 2, 6, 1 };
  for (int i = 0; i < arr.length; i++) {
   bbt.insert(arr[i]);
  }
  bbt.preOrder();
  bbt.midOrder();
  bbt.backOrder();
  bbt.levelOrder();
  System.out.println("***********搜索节点数据***********");
  System.out.println(bbt.searchTree(4).getHeight());
 }

 @Test
 public void test03() {
  BalanceBinaryTree<Integer> bbt = new BalanceBinaryTree<Integer>();
  int arr[] = { 3, 2, 1, 4, 5, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8, 9, 17 };
  for (int i = 0; i < arr.length; i++) {
   bbt.insert(arr[i]);
  }
  bbt.preOrder();
  bbt.midOrder();
  bbt.backOrder();
  bbt.levelOrder();
  System.out.println("***********删除节点数据***********");
  bbt.deleteNode(14);
  bbt.preOrder();
  bbt.midOrder();
  bbt.backOrder();
  bbt.levelOrder();
 }

}

以上是关于四平衡二叉树/AVL树的主要内容，如果未能解决你的问题，请参考以下文章

AVL树-平衡二叉树

算法小讲堂之平衡二叉树|AVL树（超详细~）

BST(二叉搜索树),AVL(平衡二叉树)RBT(红黑树)的区别

数据结构之二叉搜索树AVL自平衡树

数据结构手写平衡二叉树（AVL）

数据结构~基础2~树《二叉树二叉搜索树AVL树B树红黑树》的设计~高度平衡二叉树AVL树