算法|图的遍历-广度优先搜索(BFS)

Posted 2021-05-03 前端天一阁

什么广度优先搜索(BFS)

和树(Tree)的数据结构一样，我们也可以访问图(Graph)的所有节点。

广度优先搜索（breadth-first search，BFS）是搜索图的算法之一。

图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环，等等。

广度优先搜索会指定一个顶点，从这个顶点开始遍历图结构，遍历时先访问这个顶点的相邻顶点，然后再按队列的顺序访问相邻顶点的下一层顶点，直到到达要搜索的目标或者搜索完所有的点。

广度优先搜索是"先宽后深地访问顶点"的图搜索算法。

广度优先搜索(BFS)全过程

例如用下面的图结构，从顶点A开始搜索，直到搜索到顶点G。

广度优先搜索-图解过程1

可以知道，顶点A的相邻顶点有顶点B、顶点C、顶点D，这三个顶点，将它们视为开始搜索的顶点，加入队列。

广度优先搜索-图解过程2

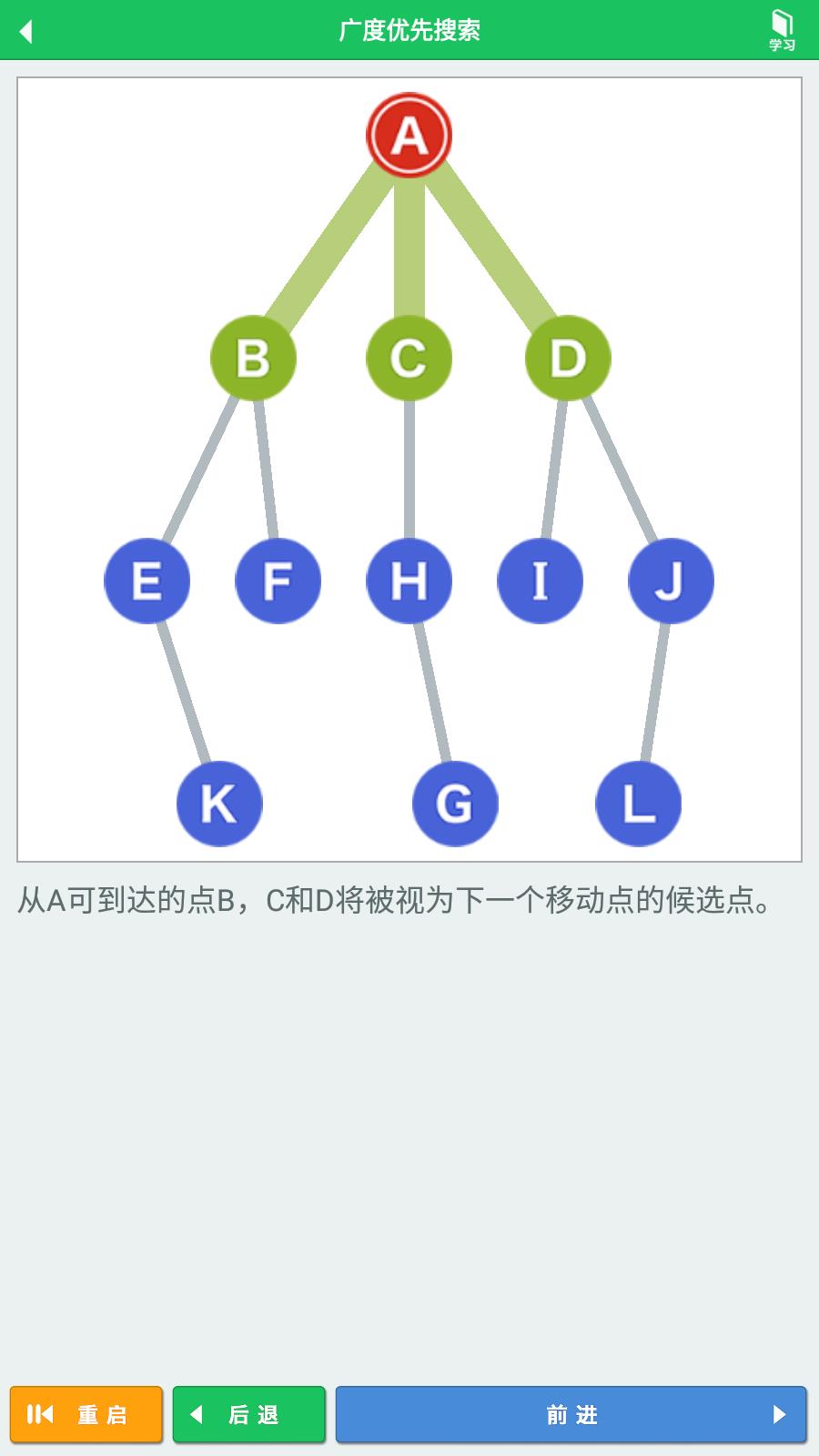
根据队列数据结构(先进先出-FIFO)的原则，我们从顶点A的三个相邻顶点(B-C-D)中，选择最先进入队列的顶点B，移动到顶点B。

广度优先搜索-图解过程3

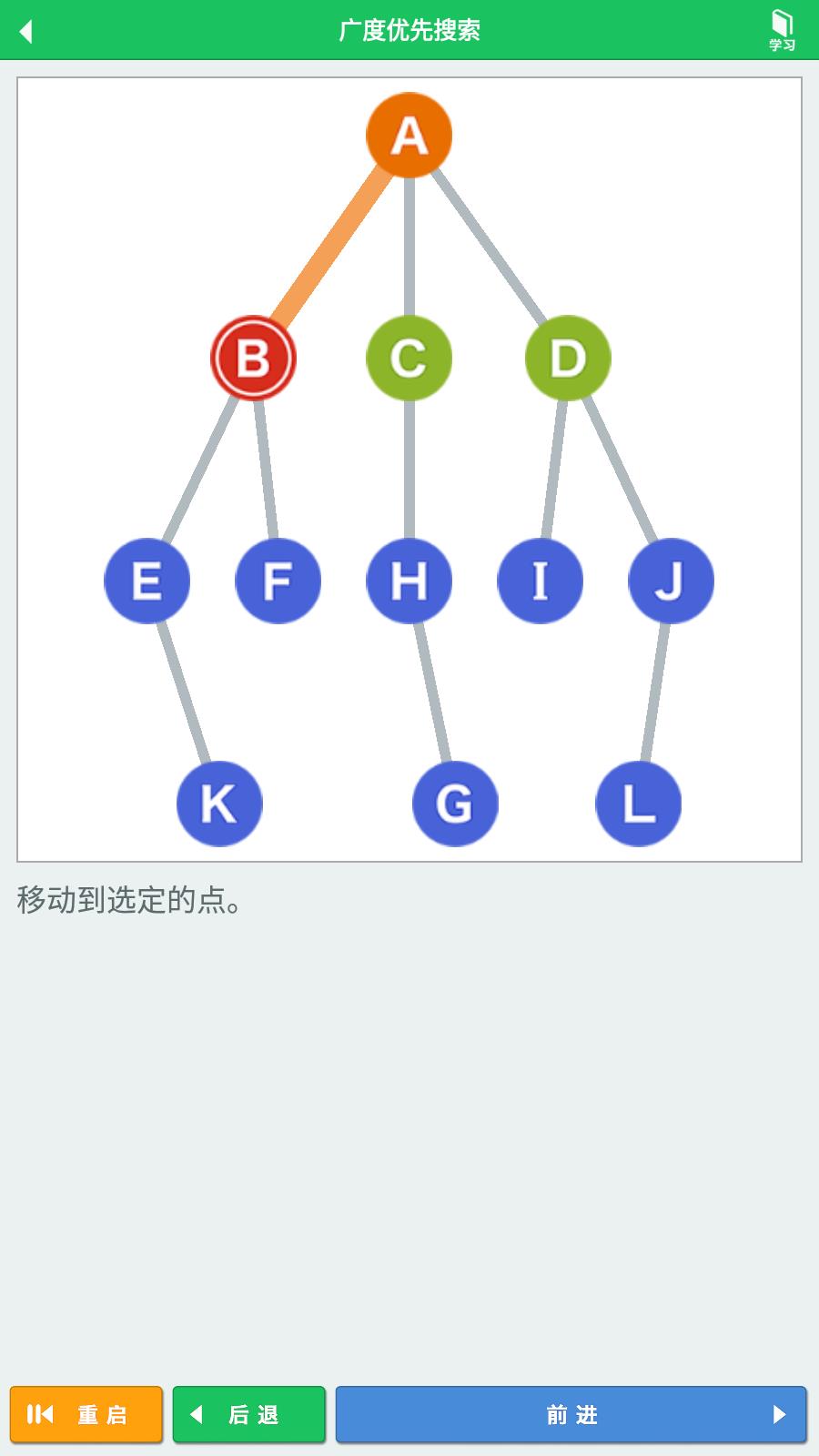
获取顶点B的相邻顶点(E-F),将他们加入队列。

广度优先搜索-图解过程4

根据队列的顺序，使用同样的方式:

到达顶点C，获取顶点C的相邻顶点(H)，将它加入队列，接着(根据队列先进先出的原则)移动到顶点D。

获取顶点D的相邻顶点(I-J)，将它加入队列，接着(根据队列先进先出的原则)移动到顶点E。

获取顶点E的相邻顶点(K)，将它加入队列，接着(根据队列先进先出的原则)移动到顶点F。

获取顶点F的相邻顶点，发现没有相邻顶点，则进行下一个顶点H的出列。

获取顶点H的相邻顶点(G),将它加入队列，接着(根据队列先进先出的原则)移动到顶点I。

获取顶点I的相邻顶点,发现没有相邻顶点，则进行下一个顶点J的出列。

获取顶点J的相邻顶点(L),将它加入队列，接着(根据队列先进先出的原则)移动到顶点K。

获取顶点K的相邻顶点,发现没有相邻顶点，则进行下一个顶点G的出列。

获取顶点G,找到需要到达的目标，结束搜索。

广度优先搜索-图解过程5

实现广度优先搜索(BFS)

代码流程

•为了标记图的顶点，我们需要提供一个表示顶点颜色的常量对象。•白色(WHITE):表示该顶点还没有被访问•灰色(GREY):表示该顶点被访问过，但并未被探索过•黑色(BLACK):表示该顶点被访问过且被完全探索过

// 广度优先算法中标记顶点的常量对象const Colors = { WHITE: 0, // 表示该顶点还没有被访问 GREY: 1, // 表示该顶点被访问过，但并未被探索过 BLACK: 2 // 表示该顶点被访问过且被完全探索过};

•并且提供一个辅助方法，用于初始化每个顶点颜色。

/** * 辅助方法:初始化每个顶点的颜色的函数 * @param {*} vertices 顶点列表 * @returns {*} 返回初始化顶点颜色后的对象 */const initializeColor = vertices => { const color = {}; for (let i = 0; i < vertices.length; i++) { color[vertices[i]] = Colors.WHITE; } return color;};

接着便是广度优先搜索算法的完整代码思路:

声明广度优先搜索算法的函数-breadthFirstSearch，接收三个参数，分别是graph(要遍历的图实例)、startVertex(开始顶点)、callback(回调函数)在函数内获取传入图实例(graph)的顶点列表、邻接表，并将图的顶点列表中的所有顶点初始化颜色为白色(表示该顶点还没有被访问)创建一个队列数据结构实例，并将startVertex(开始顶点)入队列。如果队列不为空，则进入循环，循环体内执行以下步骤:•根据入队顺序，取出队列中的一个顶点，并获取这个顶点的邻接表，并将这个顶点的颜色标识为灰色(该顶点被访问过，但并未被探索过)•如果这个顶点的邻接表不为空，则遍历这个顶点的邻接表中的顶点，遍历时，如果该邻接表的顶点是白色，则将它标识为灰色(该顶点被访问过，但并未被探索过),并将该邻接表顶点加入队列。这个顶点的邻接表探索完后，将这个顶点标识为黑色(已被访问且被完全探索)如果有传入回调函数，则执行该回调函数，回调函数会将这个顶点作为入参方法。

代码实现

/** * 图的广度优先搜索算法 * 使用到的数据结构:队列 * 概念:先宽后深地访问顶点 * @param {*} graph 要进行遍历的图(Graph 类实例) * @param {*} startVertex 开始顶点 * @param {function} callback 回调函数 */export const breadthFirstSearch = (graph, startVertex, callback) => { const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表 const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表 const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色 const queue = new Queue(); // 创建一个队列实例 queue.enqueue(startVertex); // 将开始顶点(startVertex)加入队列 while (!queue.isEmpty()) { // 如果队列不为空，则进入循环 const u = queue.dequeue(); // 按队列(先进先出)规则，取出队列里面存储的最前面的顶点，赋值给u const neighbors = adjList.get(u); // 获取顶点u的邻接表 color[u] = Colors.GREY; // 标识顶点u为灰色(该顶点被访问过，但并未被探索过) for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表 const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w if (color[w] === Colors.WHITE) { // 如果当前顶点w是白色(顶点还没有被访问) color[w] = Colors.GREY; // 则标识顶点w为灰色(该顶点被访问过，但并未被探索过) queue.enqueue(w); // 将顶点w加入队列 } } color[u] = Colors.BLACK; // 此时顶点u与其相邻顶点已经被探索，将u标识为黑色(已被访问且被完全探索) if (callback) { // 执行回调函数 callback(u); } }};

代码用例

我们初始化一个图，用于测试广度优先搜索。

let graph = new Graph();const myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];for (let i = 0; i < myVertices.length; i++) { graph.addVertex(myVertices[i]);}graph.addEdge("A", "B");graph.addEdge("A", "C");graph.addEdge("A", "D");graph.addEdge("C", "D");graph.addEdge("C", "G");graph.addEdge("D", "G");graph.addEdge("D", "H");graph.addEdge("B", "E");graph.addEdge("B", "F");graph.addEdge("E", "I");

将这个实例图，用广度优先搜索算法打印出来。

const printVertex = (value) => console.log('Visited vertex: ' + value);breadthFirstSearch(graph, vertices[0], printVertex);/** *// 最终打印结果Visited vertex: AVisited vertex: BVisited vertex: CVisited vertex: DVisited vertex: EVisited vertex: FVisited vertex: GVisited vertex: HVisited vertex: I */

广度优先搜索算法(BFS)还可以做更多

广度优先搜索算法的工作原理了解之后，它还可以做更多事情，比如使用它来搜索图顶点的最短访问路径，或者图中某个顶点的前溯点。

下面是一段利用BFS探索图实例中每个顶点的最短路径和前溯点。

代码实现

/** * 使用BFS寻找图实例每个顶点最短路径和前溯点 * @param {*} graph 要进行遍历的图(Graph 类实例) * @param {*} startVertex 开始顶点 */export const BFS = (graph, startVertex) => { const vertices = graph.getVertices(); // 获取传入参数的图，它的顶点列表 const adjList = graph.getAdjList(); // 获取传入参数的图，它的邻接表 const color = initializeColor(vertices); // 将图的顶点列表中的所有顶点初始化为白色 const queue = new Queue(); // 创建一个队列实例 const distances = {}; // 存储每个顶点的距离 const predecessors = {}; // 存储前溯点 queue.enqueue(startVertex); // 将开始顶点(startVertex)加入队列 for (let i = 0; i < vertices.length; i++) { // 遍历图的顶点列表  distances[vertices[i]] = 0; // 初始化图中每一个顶点的距离为0 predecessors[vertices[i]] = null; // 初始化图中每一个顶点的前溯点为null } while (!queue.isEmpty()) { // 如果队列不为空，则进入循环 const u = queue.dequeue(); // 按队列(先进先出)规则，取出队列里面存储的最前面的顶点，赋值给u const neighbors = adjList.get(u); // 获取顶点u的邻接表 color[u] = Colors.GREY; // 标识顶点u为灰色(该顶点被访问过，但并未被探索过) for (let i = 0; i < neighbors.length; i++) { // 循环遍历顶点u的邻接表 const w = neighbors[i]; // 取出邻接表的每个顶点，赋值给w if (color[w] === Colors.WHITE) { // 如果当前顶点w是白色(顶点还没有被访问) color[w] = Colors.GREY; // 则标识顶点w为灰色(该顶点被访问过，但并未被探索过) distances[w] = distances[u] + 1; // 给u顶点加1来增加v和w之间的距离（u是w的前溯点，distances[u]的值已经有了） predecessors[w] = u; // 发现顶点u的邻点w时，则设置w的前溯点值为u queue.enqueue(w); // 将顶点w加入队列 } } color[u] = Colors.BLACK; // 此时顶点u与其相邻顶点已经被探索，将u标识为黑色(已被访问且被完全探索) } // 最后，返回distances对象和predecessors对象 return { distances, predecessors };};

测试用例

我们初始化一个图，用于测试广度优先搜索。

let graph = new Graph();const myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];for (let i = 0; i < myVertices.length; i++) { graph.addVertex(myVertices[i]);}graph.addEdge("A", "B");graph.addEdge("A", "C");graph.addEdge("A", "D");graph.addEdge("C", "D");graph.addEdge("C", "G");graph.addEdge("D", "G");graph.addEdge("D", "H");graph.addEdge("B", "E");graph.addEdge("B", "F");graph.addEdge("E", "I");

将图实例传入BFS，探索图实例中每个顶点的最短路径和前溯点。

const shortestPathA = BFS(graph, myVertices[0]);console.log(shortestPathA.distances);console.log(shortestPathA.predecessors);/** * distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3]predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]距离(distances):distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3]顶点A到A的距离为0顶点A到B的距离为1顶点A到C的距离为1顶点A到D的距离为1顶点A到E的距离为2顶点A到F的距离为2顶点A到G的距离为2顶点A到I的距离为3前溯点(predecessors):predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]顶点A的前溯点为null顶点B的前溯点为A顶点C的前溯点为A顶点D的前溯点为A顶点E的前溯点为B顶点F的前溯点为为B顶点G的前溯点为C顶点H的前溯点为D顶点I的前溯点为E */

通过前溯点数组，我们还可以构建从顶点 A 到其他顶点的路径。

/** * 通过前溯点数组，我们还可以构建从顶点 A 到其他顶点的路径。 */const fromVertex = myVertices[0]; // 用顶点A作为源顶点// 遍历除过源顶点外的顶点for (let i = 1; i < myVertices.length; i++) { const toVertex = myVertices[i]; // 获取当前抵达的顶点的值 const path = new Stack(); // 创建一个栈来存储路径值 for ( let v = toVertex; v !== fromVertex; v = shortestPathA.predecessors[v] ) { // 追溯toVertex(当前抵达的顶点)到fromVertex(源顶点)的路径，变量v赋值为其前溯点的值 path.push(v); // v入栈 } path.push(fromVertex); // 源顶点入栈 let s = path.pop(); // 创建一个s字符串，并将源顶点赋值给它（它是最后一个加入栈中的，所以是第一个被弹出的项） while (!path.isEmpty()) { // 当栈是非空的 s += ' - ' + path.pop(); // 从栈中移出一个项并将其拼接到字符串 s 的后面 } console.log(s); // 输出路径 // 最后，就得到了从顶点 A 到图中其他顶点的最短路径（衡量标准是边的数量）。 /** * 打印结果 * A - B A - C A - D A - B - E A - B - F A - C - G A - D - H A - B - E - I  */ }