前端 | 前端函数式编程浅析

Posted 2021-05-03 维李设论

前言

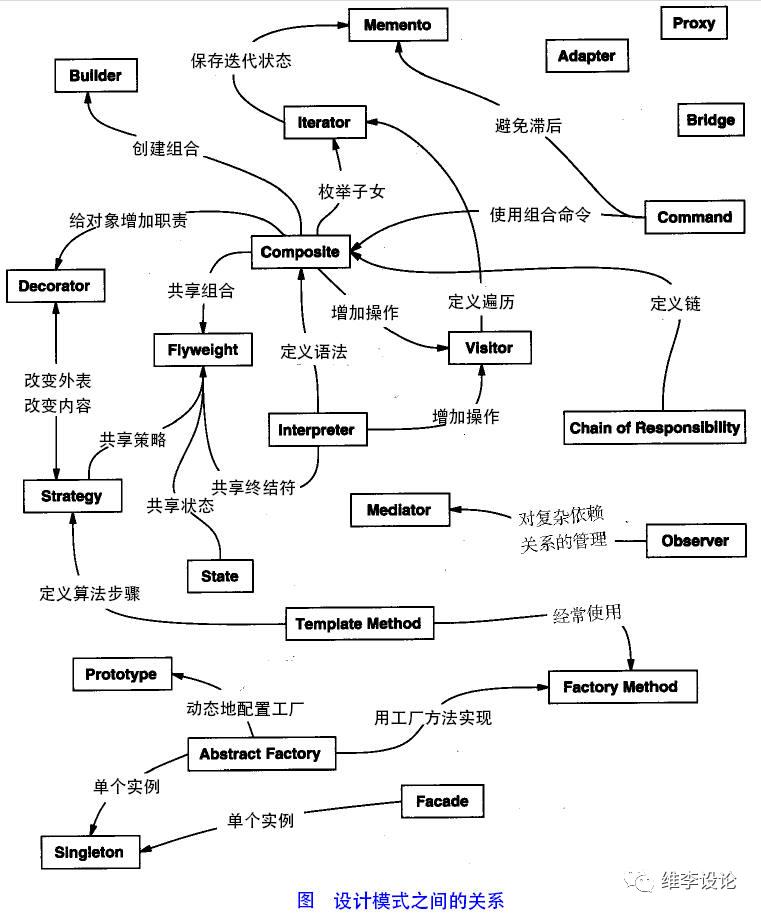
在浅析函数式编程之前，我们需要明确两个前导概念，即：编程范式（Programming Paradigm）与设计模式（Design Pattern）：

对于编程范式（Programming Paradigm），维基百科给出的定义如下：

Programming paradigms are a way to classify programming languages based on their features. Languages can be classified into multiple paradigms.

可以看出，编程范式是一种组织代码的方式，它与各大语言的特点（特别是语言设计及编译器）息息相关；

而设计模式（Design Pattern），维基百科给出的定义如下：

In software engineering, a software design pattern is a general, reusable solution to a commonly occurring problem within a given context in software design.

从定义可以得出：设计模式是一种通用的解决方案，编程范式与语言的特点是强相关的，而设计模式则是任何语言都可以根据其特点进行实现的一种通用模板

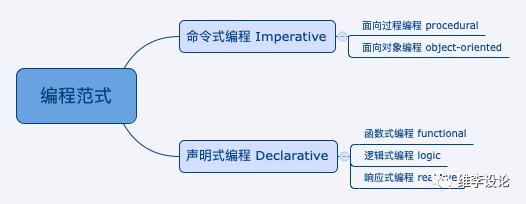
从前导的概念，我们可以了解，函数式编程是一种编程范式而不是一种设计模式，因而其与语言是强相关的，从上图可以看出，对于编程范式不能单独通过某一属性或某一边界将其区分开，尤其是现代高级语言都已基本借鉴了其他语言的特色与方法，所以，目前大多数文章或教材中对编程方式的区分方法都是做点状分析，因为其从全局明确区分确实比较困难，而常见的可以泛泛的将编程范式分为：命令式编程和声明式编程。其中命令式编程包括面向过程编程及面向对象编程（也有说面向对象编程属于元编程），而声明式编程包括函数式编程、逻辑式编程、响应式编程，我们不严谨的可以简单的将常见编程范式进行简化为上图所示分类

概念

前言中介绍了编程范式是与语言强相关的，因而函数式编程也是语言强相关的，最早的函数式编程语言是LISP，Schema语言是Lisp语言的一种方言，而现代语言比如Haskell、Clean、Erlang等也前仆后继的实现了函数式编程的特色。对于前端程序员而言，我们使用的语言是javascript或TypeScript，而后者是前者的超集，因而可以算是类JavaScript的语言使用者，对于js而言，由于其设计者Brendan Eich本身是函数式编程的拥趸，因而其设计上借鉴了Schema的函数第一公民（First Class）的理念（ps：所谓函数第一公民，是指 they can be bound to names (including local identifiers), passed as arguments, and returned from other functions, just as any other data type can.，即函数具有可以通过名称绑定、传递参数，并且可以返回其他函数的特征），这就为js的函数式编程埋下了伏笔。既然js可以实现函数式编程的特点，那么函数式编程都有什么特点，或者说怎么样组织代码就是函数式编程了？

In computer science, functional programming is a programming paradigm where programs are constructed by applying and composing functions.

维基百科中给出的定义是使用函数来组合和应用的编程范式，那么这里边最核心的就是函数，那么什么是函数？我们来看一下函数或者函数式编程在数学中的理论基础

函数

设 F 为二元关系，若任意 x ∈ domF 都存在唯一的 y ∈ ranF 使 xFy 成立，则称 F 为函数。对于函数 F，如果有 xFy，则记作 y = F(x)，并称 y 为 F 在 x 的值。

从《离散数学》中的定义可以看出，函数式是一种特殊的二元关系。简单来说，函数是连接两种实体的一种媒介关系，在编程中常见的就是 输入 -> 输出 的一种关系。从这里我们可以看出，输入什么，输出是有一个预期期望可以获得的，一般来说，我们只想处理输入的部分，对非输入的部分尽量做到不影响或者说隔离，那么当输出不符合我们的预期，即输出会影响其他输入意外的数据时候，我们就说产生了副作用（Side Effect）；而如果输入什么同时能够输出相同的结果，我们就称这样的函数为纯函数（Pure Function），这时纯函数对于它的执行环境不会带来任何的改变，我们就说这种理想情况下函数对于环境是引用透明（Referential Transparency）的。

λ演算

Lambda calculus (also written as λ-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution.

λ演算是一种形式系统（ps：数理逻辑中，将形式语言及其对应的转换规则构成的集合称为一种形式系统），这个系统中规定了特殊的形式，比如α转换和β规约：α转换（ps：α-conversion, sometimes known as α-renaming,[21] allows bound variable names to be changed.），即指允许函数调用实体（变量名、锚定标识）可以是匿名的；β规约（ps：β-reduction is defined in terms of substitution: the β-reduction of (λV.M) N is M[V := N].），即指可以将函数形式可以按某种规则进行简约替换，在es6中使用=>箭头的lamda表达式实现了α转换（this绑定规则及arguments取消）和β规约（=>与function表达替换）。根据这种演算形态，可以构建出不同的函数使用方式，常见的函数式编程中都会有柯里化函数（Curring）、偏函数（Partical Function）、组合函数（Compose）等演算形式，从而可以看出函数式编程具有如下特点：1、管道化链式调用；2、惰性求值、惰性加载；3、操作符操作，隐藏内部细节；4、不可变数据。

幺半群

设 V = < S, ο > 是代数系统，ο 为二元运算，若 ο 是可结合的，则称V是半群；若 e ∈ S 是关于 ο 运算的单位元，则称 V 为幺半群（monoid），也叫独异点，也将独异点 V 记作 V = < S, ο, e >

这里涉及到了一些范畴论（ps：不严谨的，简单来说范畴论就是将概念体系进行区分，形成一个个范畴，也就是找到对应的边界，以及在这个范畴中有自己对应的规则和描述）的概念，这里将之前说到的函数的概念进行了扩展，前面说到函数式一种特殊的二元关系，而群是有着二元运算的一些对象，在这些对象中，有一个特殊的对象e，满足一些法则（ps：不严谨的，简单理解为交换律就是一种规则），则称为单位元，也叫幺元。幺半群定义了函数二元运算的规则，对于元素A运算后仍会得到A。

函子

Let C and D be categories. A functor F from C to D is a mapping that: associates each object X in C to an Object F(X) in D; associates each morphism f: X -> Y in C to a morphism F(f): F(X) -> F(Y) in D such that the following two conditions hold: F(idx) = idF(x) for every object X in C, F(g ο f) = F(g) ο F(f) for all morphisms f: X -> Y and g: Y -> Z in C.

从定义可以看出，函子（Functor）在范畴论进行了扩展，其本质是两个范畴之间的映射关系

单子

A monad on C consists of an endofunctor T:C -> C together with two natural transformations: η: 1c -> T (where 1c denotes the identify functor on C) and μ: T2 -> T (where T2 is the functor T ο T from C to C). These are required to fulfill the following conditions (sometimes called coherence conditions): μ ο Tμ = μ ο μT (as natural transformations T3 -> T); μ ο Tη = μ ο ηT = 1T (as natural transformations T -> T; here 1T denotes the identify transformation from T to T).

从定义我们可以简单给出：单子就是自函子范畴上的幺半群，其中自函子是指映射另一个范畴也为其本身的函子。所有函数式打散之后的核心组织就可以基于单子形态的编程，因而也称为Monadic开发模型。

至此，我们了解了前端函数式编程所涉及到的底层数学依据支撑，那么接下来我们就要看一下函数式编程在前端的一些应用情况

应用

应用部分挑选了几个比较有代表性的库，旨在展现一下函数式编程的风格及特性，不会对所有源码进行分析，毕竟这些库中所运用的编程方法不止一种，所有的方法都是为人来服务的，只有思想才是最重要的，“形而上者谓之道，形而下者谓之器”

jQuery

jQuery作为一个重要的js库，虽然现在已经渐行渐远，但是在前端发展历史上其无疑是有着里程碑意义的一个代表，对于jq我们影响最深的除了其帮助我们简化了dom操作，抹平了部分浏览器接口差异外，其实其最为有影响力的当属它的链式调用，我们来看一下它是如何组织实现这一操作的：

// https://github.com/jquery/jquery/tree/1.12-stable/src/core.js
jQuery.fn = jQuery.prototype = {
    constructor: jQuery,
    selector: "",
    length: 0,
    toArray: function() {},
    get: function(num) {},
    map: function() {},
    slice: function() {},
    first: function() {},
    last: function() {},
    eq: function() {},
    end: function() {}
}

可以看出jq的链式调用通过constructor进行了一个名称的复写，利用js的特性进行了函数循环绑定从而做到了链式调用

Redux

对于redux，其中的compose及applyMiddleware都是函数式编程的一种理念体现

// https://github.com/reduxjs/redux/tree/master/src/compose.ts

export default function compose(...funcs: Funcion[]) {
    if(funcs.length === 0) {
        return <T>(arg: T) => arg
    }

    if(funcs.length === 1) {
        return funcs[0]
    }

    // compose操作
    return funcs.reduce((a,b) => (...args:any) => a(b(...args)))
}

// https://github.com/reduxjs/redux/tree/master/src/applyMiddleware.ts

export default function applyMiddleware(
  ...middlewares: Middleware[]
): StoreEnhancer<any> {
  return (createStore: StoreEnhancerStoreCreator) => <S, A extends AnyAction>(
    reducer: Reducer<S, A>,
    preloadedState?: PreloadedState<S>
  ) => {
    const store = createStore(reducer, preloadedState)

    const middlewareAPI: MiddlewareAPI = {
      getState: store.getState,
      dispatch: (action, ...args) => dispatch(action, ...args)
    }

    // map映射
    const chain = middlewares.map(middleware => middleware(middlewareAPI))
    dispatch = compose<typeof dispatch>(...chain)(store.dispatch)

    return {
      ...store,
      dispatch
    }
  }
}

React Hooks

React 16.8之后推出的react hooks，给函数式组件给予了更大的应用空间，也更符合 React认为的 ui是一种数据的设计哲学，当然react hooks也是趁着fiber架构的东风，从而将函数式理念体现到了最大，简单看一下函数式编程的一些片段，具体关于React hooks的分析，可以出门右转看一下作者之前写的这篇文章

// https://github.com/facebook/react/blob/master/packages/react-reconciler/src/ReactFiberHooks.new.js

function updateReducer<S, I, A>(
    reducer: (S, A) => S,
    initialArg: I,
    init?: I => S
): [S, Dispatch<A>] {
    const hook = updateWorkInProgressHook();
    const queue = hook.queue;
    queue.lastRenderedReducer = reducer;
    const current: Hook = (currentHook: any);
    let baseQueue = current.baseQueue;
    const pendingQueue = queue.pending;
    if (baseQueue !== null) {
        const first = baseQueue.next;
        let newState = current.baseState;

        let newBaseState = null;
        let newBaseQueueFirst = null;
        let newBaseQueueLast = null;
        let update = first;

        // 走循环

        hook.memoizedState = newState;
        hook.baseState = newBaseState;
        hook.baseQueue = newBaseQueueLast;

        queue.lastRenderedState = newState;
    }
    const dispatch: Dispatch<A> = (queue.dispatch: any);
    return [hook.memoizedState, dispatch];
}

Reactive Extensions

Reactive Extensions在各个平台都有，这里重点分析rx.js相关，其属于响应式编程，但是这里会和函数式编程结合，从而实现函数式响应式编程，即Function Reactive Programming，我们来简单看一下其flatMap的实现：

// https://github.com/ReactiveX/rxjs/tree/master/src/internal/operators/flatMap.ts

export function mergeMap<T, R, O extends ObservableInput<any>>(
  project: (value: T, index: number) => O,
  resultSelector?: ((outerValue: T, innerValue: ObservedValueOf<O>, outerIndex: number, innerIndex: number) => R) | number,
  concurrent: number = Infinity
): OperatorFunction<T, ObservedValueOf<O> | R> {
  if (isFunction(resultSelector)) {
    // DEPRECATED PATH
    return mergeMap((a, i) => map((b: any, ii: number) => resultSelector(a, b, i, ii))(innerFrom(project(a, i))), concurrent);
  } else if (typeof resultSelector === 'number') {
    concurrent = resultSelector;
  }

  return operate((source, subscriber) => mergeInternals(source, subscriber, project, concurrent));
}

Lodash

lodash作为一款工业级的工具库，其对原本js中的各种操作api都进行了扩展，我们来看一下其进行分割元素的一些实现：

// https://github.com/lodash/lodash/take.js

function take(array, n=1) {
  if (!(array != null && array.length)) {
    return []
  }
  return slice(array, 0, n < 0 ? 0 : n)
}

Ramda

作为真正的lamda演算的一个js库，其算是基本实现了所有lamda演算的需求

// https://github.com/ramda/ramda/tree/master/source/curryN.js

export default function _curryN(length, received, fn) {
  return function() {
    var combined = [];
    var argsIdx = 0;
    var left = length;
    var combinedIdx = 0;
    while (combinedIdx < received.length || argsIdx < arguments.length) {
      var result;
      if (combinedIdx < received.length &&
          (!_isPlaceholder(received[combinedIdx]) ||
           argsIdx >= arguments.length)) {
        result = received[combinedIdx];
      } else {
        result = arguments[argsIdx];
        argsIdx += 1;
      }
      combined[combinedIdx] = result;
      if (!_isPlaceholder(result)) {
        left -= 1;
      }
      combinedIdx += 1;
    }
    return left <= 0
      ? fn.apply(this, combined)
      : _arity(left, _curryN(length, combined, fn));
  };
}

总结

函数式编程作为一种编程范式，其意义不仅仅在于业务的具体实现，更重要的在于整个业态的发展趋势，流式渲染，前后端同构，结合serverless、faas等相关，同时提供给flink等大数据相关的一些新的接入方案，私以为这才是函数式编程如今在前端如此备受关注的更加前瞻的视角；同时，我们也不应该过渡的依赖函数式编程，认为所有的代码组织都得以函数式编程为主，这样过犹不及，并非是一种好的编程理念，正如“软件工程里没有银弹（No Silver Bullet）”一样，所有方法和模式都是为人服务的，思想才是最重要的，方法只是手段，共勉！

参考

• 前端函数式演进

• JavaScript函数式编程指南

• 离散数学（第2版）

• 范畴论

• 范畴论学习笔记

• Category Theory Course

• Category Theory

• 范畴论简史

• Stanford CS107 Programming Paradigms

• Programming paradigm

• Software design pattern

• JavaScript at 20

• 函数式编程入门教程