C++ 利用硬件加速矩阵乘法

Posted 2021-05-03 C和C加加

来源：blog.csdn.net/whereisherofrom

1.矩阵乘法定义

2.矩阵类封装

我们用 C++封装了一个n × m 的矩阵类，用二维数组来存储数据，定义如下：

#define MAXN 1000#define LL __int64
class Matrix {private: int n, m; LL** pkData;public: Matrix() : n(0), m(0) { pkData = NULL; } void Alloc() { pkData = new LL *[MAXN]; // 1) for (int i = 0; i < MAXN; ++i) { pkData[i] = new LL[MAXN]; } } void Dealloc() { if (pkData) { for (int i = 0; i < MAXN; ++i) { // 2) delete [] pkData[i]; } delete[] pkData; pkData = NULL; } }};

3.矩阵乘法实现

（1）ijk 式

最简单的矩阵乘法实现如下：

class Matrix { ...public: void Multiply_ijk(const Matrix& other, Matrix& ret) { // assert(m == other.n); ret.Reset(n, other.m); int i, j, k; for (i = 0; i < n; i++) { for (j = 0; j < other.m; j++) { for (k = 0; k < m; k++) { ret.pkData[i][j] += pkData[i][k] * other.pkData[k][j]; } } } }};

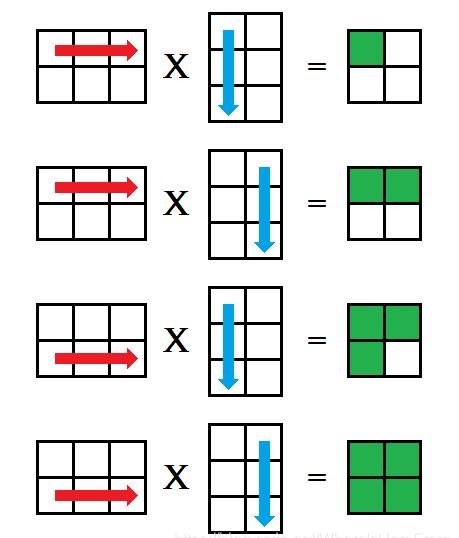
这种方法被称为 ijk 式，对矩阵乘法 A × B = C，枚举 A 的每一行，再枚举 B 的每一列，分别对应相乘后放入矩阵 C的对应位置中，如下图所示；

（2）ikj 式

对上述算法进行一些改进，交换两个内层循环的位置，得到如下算法：

class Matrix { ...public: void Multiply_ikj(const Matrix& other, Matrix& ret) { // assert(m == other.n); ret.Reset(n, other.m); int i, j, k; for (i = 0; i < n; i++) { for (k = 0; k < m; k++) { LL v = pkData[i][k]; for (j = 0; j < other.m; j++) { ret.pkData[i][j] += v * other.pkData[k][j]; } } } }};

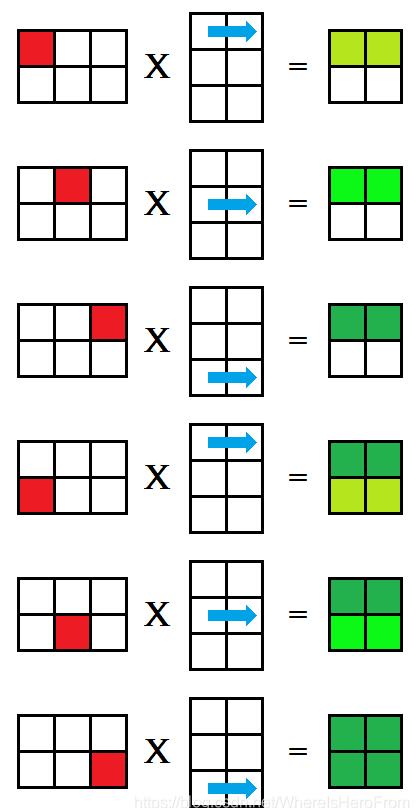
这种方法被称为ikj 式，对矩阵乘法 A × B = C ，行优先枚举 A的每一个格子，再枚举 B的每一行，分别对应相乘后放入矩阵 C的对应位置中，每次相乘得到的 C 都是部分积，如下图所示，用绿色的深浅来表示这个值是否已经完整求得；

（3）kij 式

对上述算法再进行一些改进，交换两个外层循环的位置，得到如下算法：

class Matrix { ...public: void Multiply_kij(const Matrix& other, Matrix& ret) { // assert(m == other.n); ret.Reset(n, other.m); int i, j, k; for (k = 0; k < m; k++) { for (i = 0; i < n; i++) { LL v = pkData[i][k]; for (j = 0; j < other.m; j++) { ret.pkData[i][j] += v * other.pkData[k][j]; } } } }};

这种方法被称为kij 式，对矩阵乘法 A × B = C ，列优先枚举 A的每一个格子，再枚举 B的每一行，分别对应相乘后放入矩阵 C 的对应位置中，每次相乘得到的 C 都是部分积，如下图所示，用绿色的深浅来表示这个值是否已经完整求得；

4.时间测试

5.原理分析

• 原因是因为 CPU 访问内存的速度比 CPU 计算速度慢得多，为了解决速度不匹配的问题，在 CPU 与 内存 之间加了高速缓存cache。高速缓存 cache 的存在大大提高了 CPU 访问数据的速度。但是当内存访问不连续的时候，就会导致 cache 命中率降低，所以为了加速，就要尽可能使内存访问连续，即不要跳来跳去。

• 矩阵

6.最后结论

运行速度：

ikj≈kij>ijk

简单分享快乐学习，如有错误请多包涵！

PS：如果没有你的关注，那我所做的将毫无意义！欢迎分享，点赞，在看。