到底什么是谱聚类算法?
Posted 小白学视觉
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了到底什么是谱聚类算法?相关的知识,希望对你有一定的参考价值。
重磅干货,第一时间送达
谱聚类算法是目前最流行的聚类算法之一,其性能及适用场景优于传统的聚类算法如k-均值算法,本文对谱聚类算法进行了详细总结,内容主要参考论文《A Tutorial on Spectral Clustering》,下载链接:https://github.com/zhangleiszu/machineLearning,若对谱聚类算法有不理解的地方,欢迎交流。
1. 谱聚类模型的优化思想
2. 图的表示方法
3. 邻接矩阵的表示方法
4. 拉普拉斯矩阵定义及其属性
5. 无向图切图的含义
6. 谱聚类算法原理
7. 谱聚类算法流程
8. 拉普拉斯矩阵的选择
9. 簇类个数的选择
10. 谱聚类算法与k均值算法比较
11. 谱聚类算法的参数择优
12. 小结
上文提到若簇内的相似度高且簇间的相似度低,则聚类性能较好,因此优化聚类模型的标准是提高簇类相似度高且降低簇间的相似度。
谱聚类模型的优化思想也是基于此标准,下面定性给出谱聚类模型的目标函数:
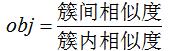
谱聚类模型优化的方法是最小化该目标函数。
谱聚类是一种基于图论的聚类算法,在介绍谱聚类算法原理之前,首先介绍下图的相关概念。
图G(graph)是由点的集合V(vertex)和边的集合E(edge)组成,即G=(V,E),其中V为数据集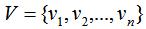 ,E为样本点
,E为样本点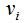 与样本点
与样本点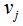 的权重,用
的权重,用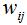 表示,
表示,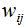 等于0表示样本点
等于0表示样本点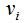 与样本点
与样本点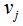 没有连接。
没有连接。
因此对于容量为n的数据集,其图的有向邻接矩阵W表示为: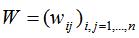 ,无向图的权重
,无向图的权重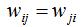
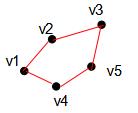
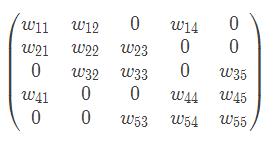
上图的无向权重W表示为:
定义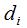 为样本点
为样本点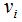 的度:
的度:
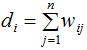
样本点度的含义为所有与该样本点连接的权重之和。
数据集所有样本点的度定义为度矩阵D:
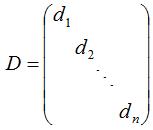
矩阵D是对角矩阵且非对角元素均为0。
下面定义指示向量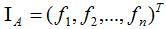 ,下标A表示数据集V的一个子集,若样本点
,下标A表示数据集V的一个子集,若样本点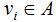 ,则
,则
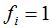 ,反之
,反之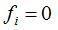 。
。
如下图,数据集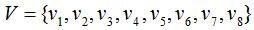 包含两个子集A1和A2:
包含两个子集A1和A2:
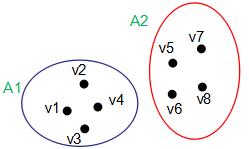
因此指示向量:
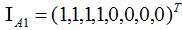
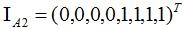
易知不同子集的指示向量相互正交。
我们有两种定义子集A大小的方法:
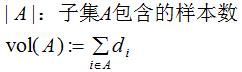
上节介绍邻接矩阵的权重即是样本间的相似度,衡量相似度的方法有 ε邻近法,K近邻法和全连接法,下面一一介绍这三种方法。
3.1 ε-邻近法
若样本间的距离小于 ε,则用权重 ε连接两个样本;样本间的距离大于ε,则连接两个样本的权重等于0。因此,图的无向权重表达式如下:
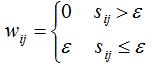
其中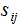 是样本i与样本j的距离。
是样本i与样本j的距离。
ε近邻描述样本间的权重只有ε和0,缺失了很多信息 。
3.2 k近邻法
k近邻法只考虑离该样本点最近的k个样本的权重,不在k近邻范围的样本,权重为0,然而这种定义方法会导致有向邻接矩阵,因为该矩阵并非对称矩阵,比如样本点j是样本点i的k近邻,样本点i并不一定是样本点j的k近邻。
为了使邻接矩阵是对称矩阵,我们对k近邻法有两种改进方法:第一种方法是若样本点j是样本点i的k近邻或样本点i是样本点j的k近邻,则该样本间的权重不为0,数学表达式如下:
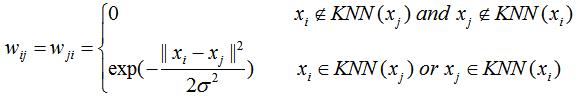
第二种方法是若样本点互为k近邻,则该样本间的权重不为0,数学表达式如下:
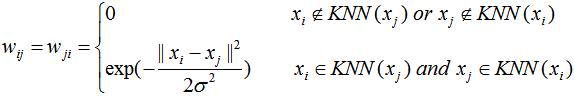
3.3 全连接法
全连接法直接用相似度衡量所有的样本间权重,因此样本间的权重都大于0,常用高斯相似函数评价样本间的权重。数学表达式如下:
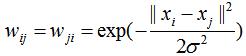
ε-邻近法与k近邻法在密度分布不均的聚类任务中有较大的误差,实际项目中常用全连接法构建邻接矩阵,邻接矩阵的权重常用高斯相似函数。全连接法的缺点是构建的邻接矩阵并非稀疏矩阵,导致计算量的增加。
拉普拉斯矩阵L是谱聚类算法的基础,本节介绍下面两种拉普拉斯矩阵及其属性,分别是非标准化的拉普拉斯矩阵和标准化的拉普拉斯矩阵。
4.1 非标准化的拉普拉斯矩阵
非拉普拉斯矩阵定义为度矩阵D与邻接矩阵W的差,表达式如下:
L = D - W
度矩阵D和邻接矩阵W的定义请参考二三节。
非标准化的拉普拉斯矩阵有如下属性:
(1)对于任意的n维向量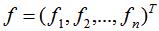 ,有:
,有:
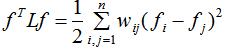
证明:
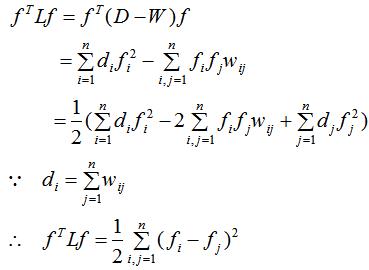
(2)由于D和W是对称矩阵,拉普拉斯矩阵L也是对称矩阵,由属性(1)得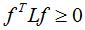 ,即拉普拉斯矩阵L是半正定矩阵。
,即拉普拉斯矩阵L是半正定矩阵。
(3)拉普拉斯矩阵L的最小特征值为0,相应的特征向量是全为1的向量。
证明:
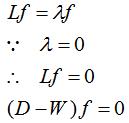
由上式可得:f是全为1的特征向量,即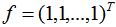 。
。
(4)L为半正定的对称矩阵,因此L有n个非负的实数特征值,即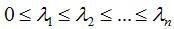 。
。
(5)假设图G是无向权重图,拉普拉斯矩阵的特征值为0时,对应的特征向量个数等于连通子集的个数,且该特征向量等于指示向量。假设下图G可划分为3个连通子集Ai(i=1,2,3):
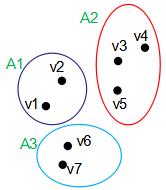
即图G的拉普拉斯矩阵L特征值为0的特征向量个数为3,且该特征向量等于指示向量,结果为:
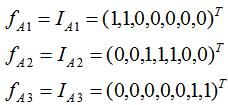
4.2 标准化的拉普拉斯矩阵
我们有两种标准化拉普拉斯矩阵的定义方法,分别为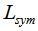 和
和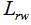 ,定义为:
,定义为:
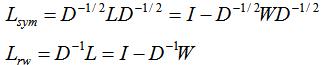
下面总结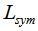 和
和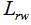 的几个重要属性:
的几个重要属性:
(1)对于任意n维向量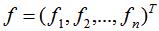 ,有:
,有:
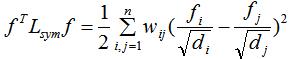
证明:
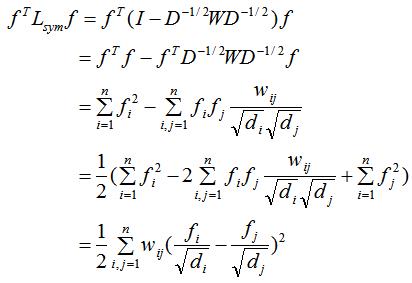
(2)若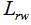 的特征值和特征向量分别为λ和v,那么
的特征值和特征向量分别为λ和v,那么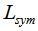 的特征值为λ时对应的特征向量w满足:
的特征值为λ时对应的特征向量w满足:
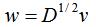
证明:
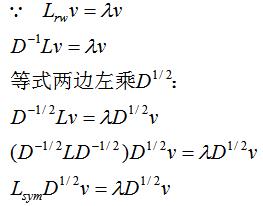
因此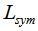 特征值为λ时的特征向量为
特征值为λ时的特征向量为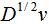 。
。
(3)若拉普拉斯矩阵L满足如下等式:
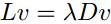
上式左乘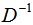 ,可得
,可得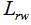 的特征值和特征向量分别为λ和v。
的特征值和特征向量分别为λ和v。
(4)若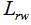 的特征值和特征向量分别为0和全为1的向量L,那么可由属性(2)可得
的特征值和特征向量分别为0和全为1的向量L,那么可由属性(2)可得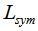 的特征值为0时的特征向量为
的特征值为0时的特征向量为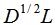 。
。
(5)由属性(1)(2)可得,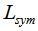 和
和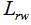 有n个非负的实数特征值
有n个非负的实数特征值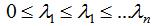 。
。
(6)假设图G是无向权重图,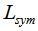 和
和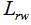 特征值为0时的特征向量个数k等于图的连通子集的个数Ai(i=1,2,...k),
特征值为0时的特征向量个数k等于图的连通子集的个数Ai(i=1,2,...k),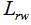 的特征向量是指示向量
的特征向量是指示向量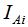 ,
,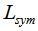 的特征向量是
的特征向量是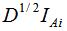 。
。
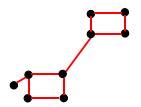
数据集的聚类可看成是无向图的切分,假设图G切分后包含两个连通的子集A,B,则AB之间的切图权重为:
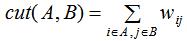
其中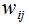 表示图G的邻接矩阵。
表示图G的邻接矩阵。
若对图G切分成k个连通子集Ai(i=1,2,...,k),最简单的方法是最小化下式:
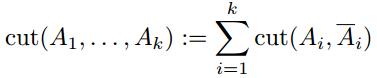
其中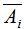 表示
表示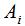 的补集。
的补集。
这种切分法只考虑了最小化簇间的相似度并没有考虑簇内的相似度,因此这种切分标准并不准确,如对上图G进行切分,得到如下的切分结果:
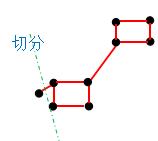
这种切分后产生的两个簇类(子集)明显是错误的,因此需要对切分方法进行优化,下一节将介绍谱聚类算法的两种切图方法。
上一节的切图方法只考虑了簇间的相似度,导致每个簇类包含的样本数差别极大,如上一节的切分结果。因此需要用每个子集的大小对上一节的切分方法进行标准化,第二节介绍有两种定义子集大小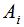 的方法,根据这这两种定义引出最常用的切图方法:RatioCut切图和Ncutt切图,本节假设簇类个数为k,即切图后的子集个数为k。
的方法,根据这这两种定义引出最常用的切图方法:RatioCut切图和Ncutt切图,本节假设簇类个数为k,即切图后的子集个数为k。
6.1 RatioCut切图
若定义子集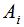 大小为子集包含的样本个数
大小为子集包含的样本个数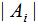 ,则RatioCut切图方法为:
,则RatioCut切图方法为:
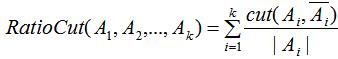
最小化上式得到最优的切分结果,如何最小化?这就要用到之前介绍的拉普拉斯矩阵和指示向量。
由指示向量定义可知指示向量个数与簇类个数相等且指示向量维度与样本数相等,因此我们定义k个指示向量
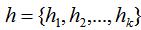 ,n维指示向
,n维指示向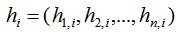 ,表达式如下:
,表达式如下:
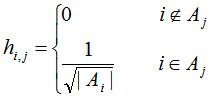
易知指示向量是单位正交向量。
看到单位正交向量,我们是不是想到了矩阵的特征值分解,下面我们计算拉普拉斯矩阵L的特征向量是指示向量时的特征值:
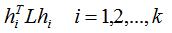
由第四节拉普拉斯矩阵的第一个属性可知:
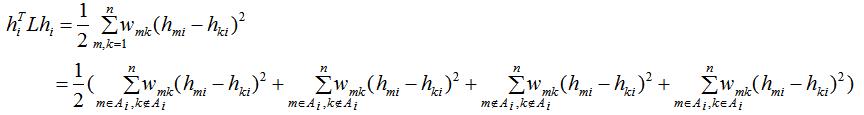
由指示向量的定义,上式等价于:
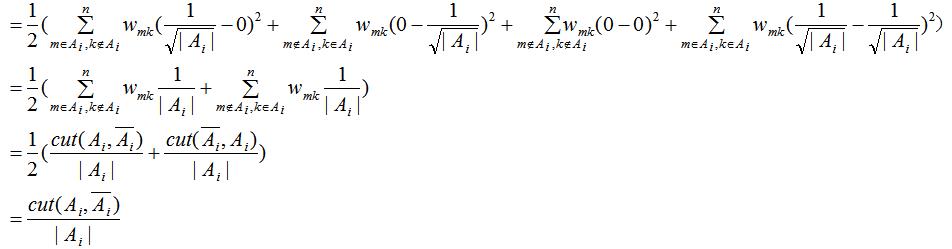
根据上式等式可得:
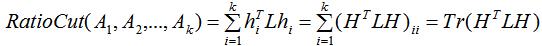
其中Tr表示取矩阵的迹。
因此最小化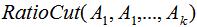 等价于:
等价于:

只需要求矩阵L的前k个最小的特征值以满足切图的最小化,取相应的k个n维特征向量组成的矩阵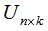 ,对该矩阵进行k均值聚类算法,得到聚类结果
,对该矩阵进行k均值聚类算法,得到聚类结果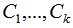 。
。
6.2 Ncutt切图
若定义子集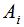 大小为
大小为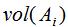 ,则RatioCut切图方法为:
,则RatioCut切图方法为:
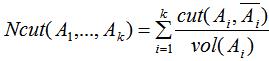
我们定义n维指示向量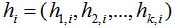 ,表达式如下:
,表达式如下:
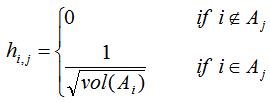
我们同样计算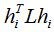 的值:
的值:
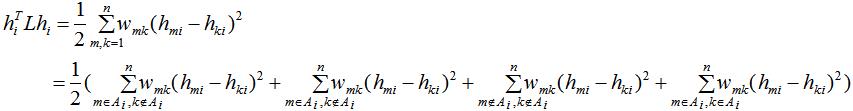
由指示向量的性质得:
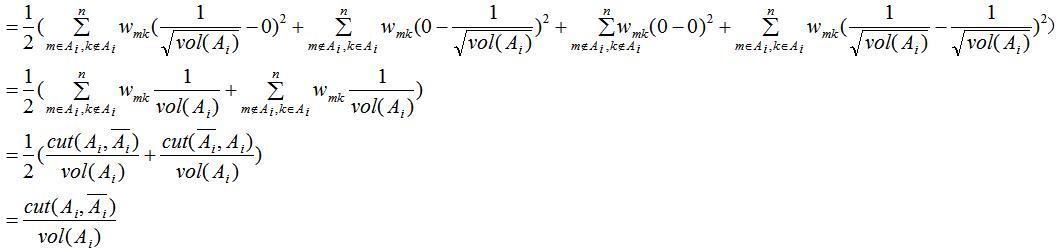
由上式推导可得:
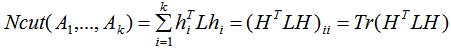
由于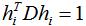 ,有
,有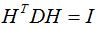 ,其中I为单位向量。
,其中I为单位向量。
因此,最小化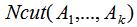 等价于:
等价于:
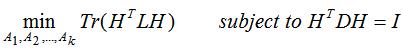
为了方便计算,需要将指示向量组成的矩阵转换为单位正交矩阵:
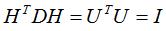
其中U为单位正交矩阵,得:
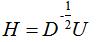
因此,最小化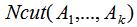 等价于:
等价于:
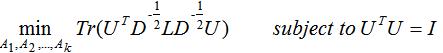
因此只需要求矩阵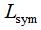 (
(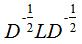 )的前k个最小的特征值满足切图的最小化,取相应的k个n维特征向量组成的矩阵
)的前k个最小的特征值满足切图的最小化,取相应的k个n维特征向量组成的矩阵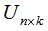 ,并对该矩阵的每行进行标准化,最后对该标准化矩阵进行k均值聚类算法得到聚类结果
,并对该矩阵的每行进行标准化,最后对该标准化矩阵进行k均值聚类算法得到聚类结果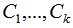 。
。
或者求矩阵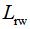 的前k个最小的特征值对应的特征向量,除了不需要进行行标准化外,算法步骤与
的前k个最小的特征值对应的特征向量,除了不需要进行行标准化外,算法步骤与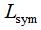 一致。
一致。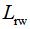 的特征向量v可以通过属性3求解:
的特征向量v可以通过属性3求解:
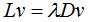
由于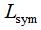 和
和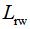 是标准化的拉普拉斯矩阵,因此 Ncutt切图也称为标准化的谱聚类算法,RatioCut切图称为非标准化的谱聚类算法。
是标准化的拉普拉斯矩阵,因此 Ncutt切图也称为标准化的谱聚类算法,RatioCut切图称为非标准化的谱聚类算法。
谱聚类算法包括非标准化的谱聚类算法和标准化的谱聚类算法,本节介绍这两种谱聚类的算法步骤。输入:相似矩阵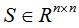 ,簇类个数等于k
,簇类个数等于k
非标准化的谱聚类算法流程:
1)计算邻接矩阵W和度矩阵D;
2)计算非标准化的拉普拉斯矩阵L;
3)计算矩阵L的k个最小特征值对应的n维特征向量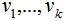 ;
;
4)k个n维特征向量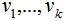 组成n×k维的矩阵M;
组成n×k维的矩阵M;
5)每一行表示一个样本,对该n个样本进行k均值聚类算法,得到聚类结果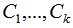 。
。
标准化的谱聚类(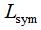 )算法流程:
)算法流程:
1)计算邻接矩阵W和度矩阵D;
2)计算标准化的拉普拉斯矩阵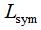 ;
;
3)计算矩阵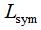 的k个最小特征值对应的n维特征向量
的k个最小特征值对应的n维特征向量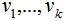 ;
;
4)k个n维特征向量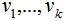 组成n×k维的矩阵M;
组成n×k维的矩阵M;
5)行标准化矩阵M:
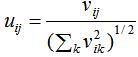
6)每一行表示一个样本,对该n个样本进行k均值聚类算法,得到聚类结果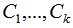 。
。
标准化的谱聚类(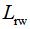 )算法流程:
)算法流程:
1)计算邻接矩阵W和度矩阵D;
2)计算标准化的拉普拉斯矩阵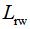 ;
;
3)计算矩阵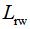 的k个最小特征值对应的n维特征向量
的k个最小特征值对应的n维特征向量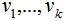 ,通过下式求解特征向量:
,通过下式求解特征向量:
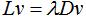
4)k个n维特征向量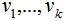 组成n×k维的矩阵M;
组成n×k维的矩阵M;
5)每一行表示一个样本,对该n个样本进行k均值聚类算法,得到聚类结果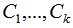 。
。
本文介绍了三种拉普拉斯矩阵的算法,选择哪一种算法是谱聚类的一个基本问题。如果图是规则的且大多数样本点的度近似相等,选择任何一种拉普拉斯矩阵都是可行的。如果图中大多数样本点的度相差较大,建议使用标准化的拉普拉斯矩阵。标准化的拉普拉斯矩阵建议使用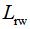 ,由标准化的拉普拉斯矩阵属性可知:若
,由标准化的拉普拉斯矩阵属性可知:若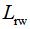 的特征向量是指示向量
的特征向量是指示向量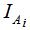 ,则
,则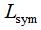 的特征向量是指示向量与
的特征向量是指示向量与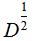 的乘积,这可能会带来不可预知的误差,因此标准化的拉普拉斯矩阵使用
的乘积,这可能会带来不可预知的误差,因此标准化的拉普拉斯矩阵使用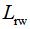 。
。
为什么标准化的拉普拉斯矩阵比非标准化的拉普拉斯矩阵好?
原因:非标准化的拉普拉斯矩阵对应RatioCut切图,RatioCut切图描述簇内的相似度为簇内包含的样本个数|A|,标准化的拉普拉斯矩阵对应Ncutt切图,Ncutt切图描述簇内的相似度为vol(A)。由于vol(A)比|A|更能体现簇内的相似度,因此选择标准化的拉普拉斯矩阵。
谱聚类算法的第一个问题是簇类个数的选择,常用的方式是使用启发式的特征值差值搜索(eigengap heuristic),含义:若前k个特征值很小,且第k+1个特征值与前一个特征值相差比较大,则簇类个数选择k。为什么选择前k个最小的特征值作为簇类个数?我们假设图G可切分为k个完全没有交集的连通子集,那么有k个特征值等于0,第k+1个特征值大于0。因此可以设想特征值越小聚类的性能亦越好,选择特征值很小的个数作为簇类个数。如下图不同簇类的样本分布:
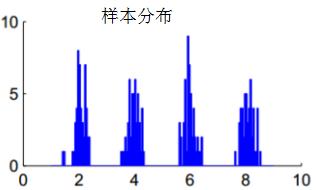
我们对服从上图分布的样本集选择10近邻法构建相似矩阵,画出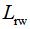 的前10个最小的特征值图:
的前10个最小的特征值图:
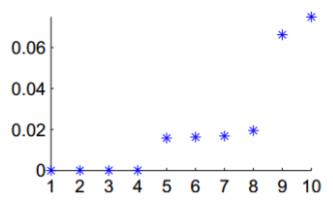
由上图可知,前4个特征值等于0,即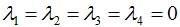 ,第5个特征值大于0且与前一个特征值相差较大,因此选择簇类个数为4,符合样本集的分布理论。
,第5个特征值大于0且与前一个特征值相差较大,因此选择簇类个数为4,符合样本集的分布理论。
若不同簇类的样本分布有重叠,如下图:
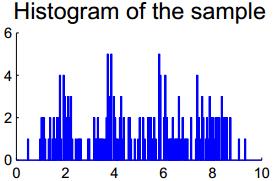
我们画出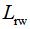 的前10个最小的特征值图:
的前10个最小的特征值图:
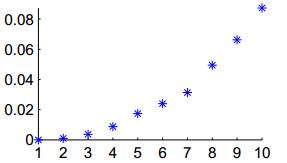
由上图可知,特征值相差不明显,可能选择k=3或k=4。若不同簇类的样本分布存在严重的重叠,这种选择k值的算法也会给出模糊的结果。
在各向异性的数据集和非凸数据集的表现很差,谱聚类算法可以很好的处理这类数据集。各向异性的数据集聚类对比:
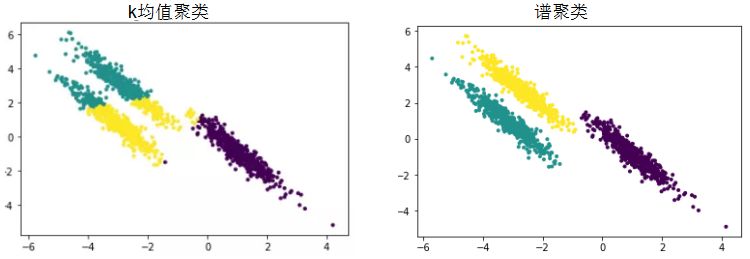
非凸数据集的聚类对比:
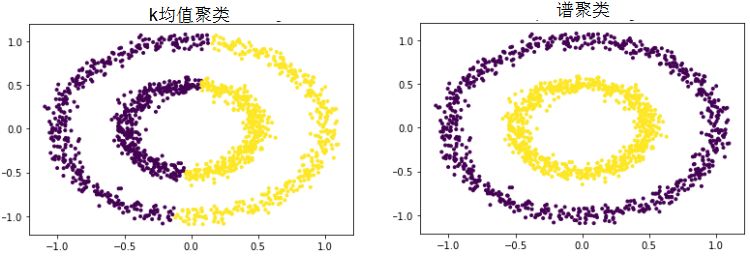
# 非凸数据集
from sklearn import datasets
from sklearn import cluster
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
plt.figure(figsize=[6,6])
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5, noise=.05)
plt.scatter(noisy_circles[0][:,0],noisy_circles[0][:,1],marker='.')
plt.title("non-convex datasets")
plt.show()
# k=2训练数据,k-means聚类算法
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(noisy_circles[0])
plt.scatter(noisy_circles[0][:, 0], noisy_circles[0][:, 1], marker='.',c=y_pred)
plt.title("k-means clustering")
plt.show()
# spectralClustering聚类算法
y_pred = cluster.SpectralClustering(n_clusters=2,affinity="nearest_neighbors").fit_predict(noisy_circles[0])
plt.scatter(noisy_circles[0][:, 0], noisy_circles[0][:, 1], marker='.',c=y_pred)
plt.title("spectralClustering")
plt.show()
为了使聚类结果可视化,我们生成各向异性的二维数据集:
random_state = 170
n_samples =1500
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)
plt.figure()
plt.scatter(X_aniso[:,0],X_aniso[:,1],marker='.')
plt.show()
根据上一节的可视化图设置k=3,使用默认的谱聚类算法参数的聚类效果:
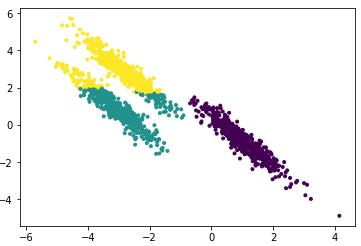
我们利用Caliniski-Harabaz指数评价聚类结果:
# 参数择优
from sklearn import metrics
for index, gamma in enumerate((0.01,0.1,1,10,15)):
y_pred = cluster.SpectralClustering(n_clusters=3, gamma=gamma).fit_predict(X_aniso)
print("Calinski-Harabasz Score with gamma=", gamma, "score:", metrics.calinski_harabaz_score(X, y_pred))
#>
Calinski-Harabasz Score with gamma= 0.01 score: 5506.749740179376
Calinski-Harabasz Score with gamma= 0.1 score: 875.228683610666
Calinski-Harabasz Score with gamma= 1 score: 3023.915226286713
Calinski-Harabasz Score with gamma= 10 score: 10633.868943793219
Calinski-Harabasz Score with gamma= 15 score: 10633.868943793219
从上面的结果分析,我们粗略的知道gamma在10附近有较好的聚类性能:
# 在10附近找寻最优参数
for gamma in np.linspace(9,11,5):
y_pred = cluster.SpectralClustering(n_clusters=3, gamma=gamma).fit_predict(X_aniso)
print("Calinski-Harabasz Score with gamma=", gamma,"score:", metrics.calinski_harabaz_score(X, y_pred))
#>
Calinski-Harabasz Score with gamma= 9.0 score: 10454.66879752764
Calinski-Harabasz Score with gamma= 9.5 score: 10454.66879752764
Calinski-Harabasz Score with gamma= 10.0 score: 10633.868943793219
Calinski-Harabasz Score with gamma= 10.5 score: 10633.868943793219
Calinski-Harabasz Score with gamma= 11.0 score: 10633.868943793219
因此,我们设置rbf核的参数gamma为10
y_pred = cluster.SpectralClustering(n_clusters=3,gamma=10).fit_predict(X_aniso)
plt.scatter(X_aniso[:,0],X_aniso[:,1],c =y_pred,marker='.')
plt.show()
聚类效果如下图:
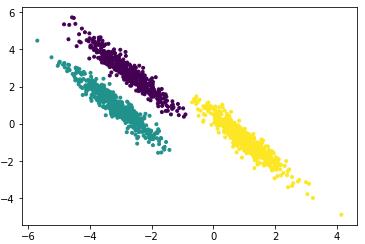
交流群
以上是关于到底什么是谱聚类算法?的主要内容,如果未能解决你的问题,请参考以下文章