二叉树(上)
Posted 编程加油站
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树(上)相关的知识,希望对你有一定的参考价值。
一、什么是树?
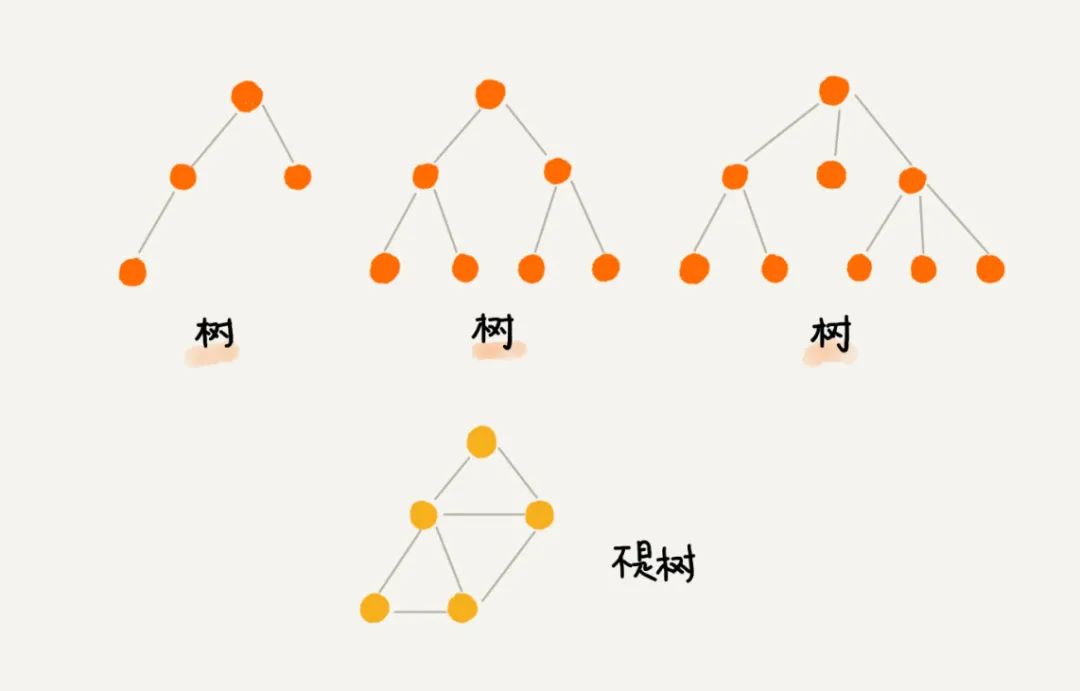
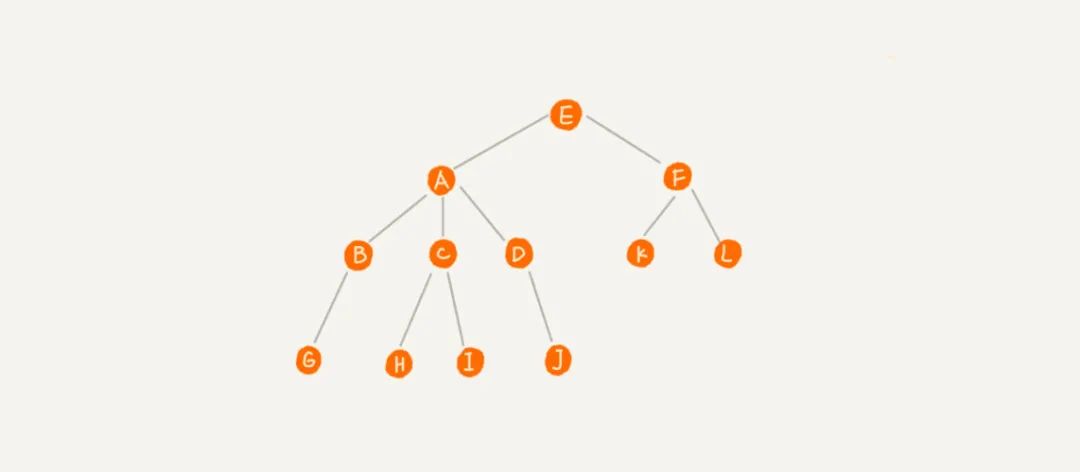

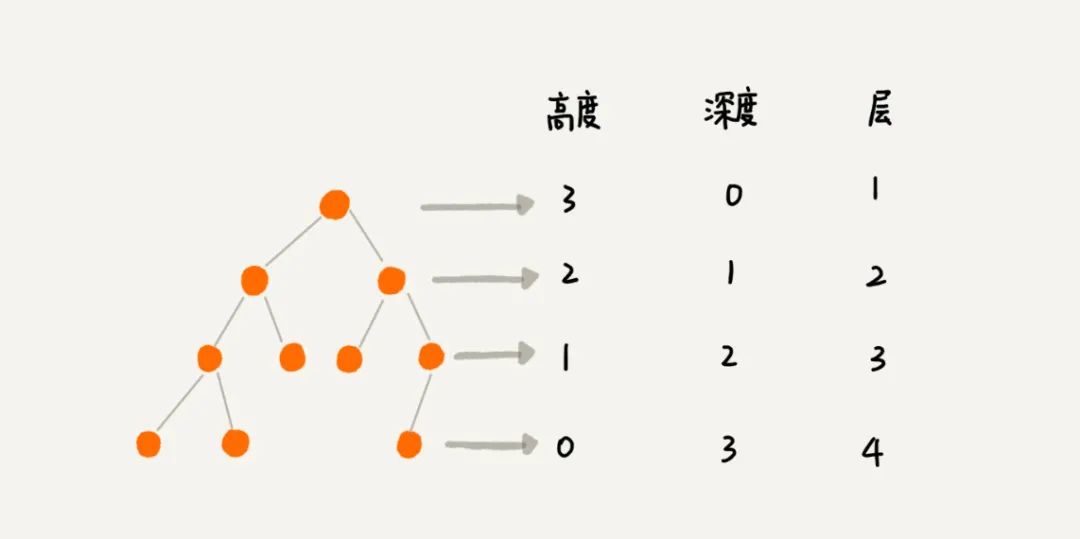
二、二叉树
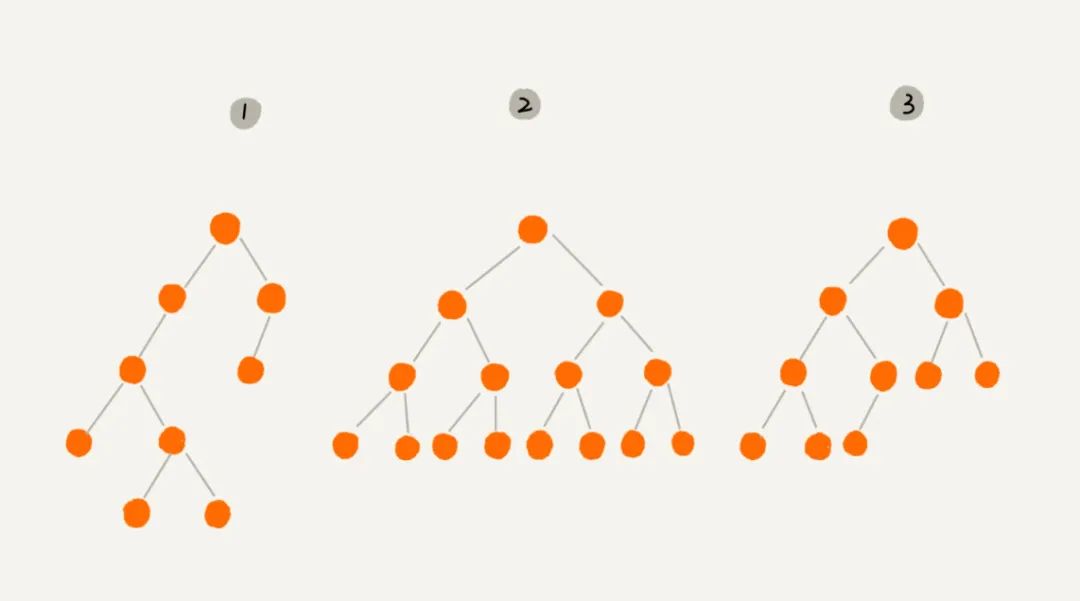
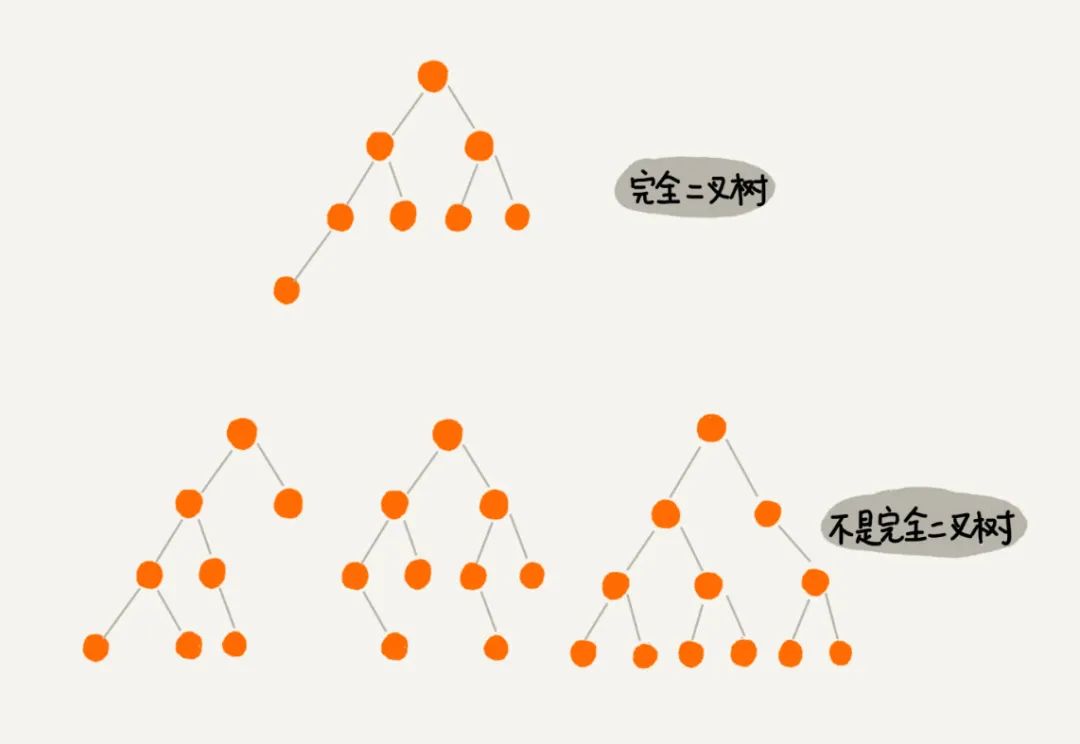
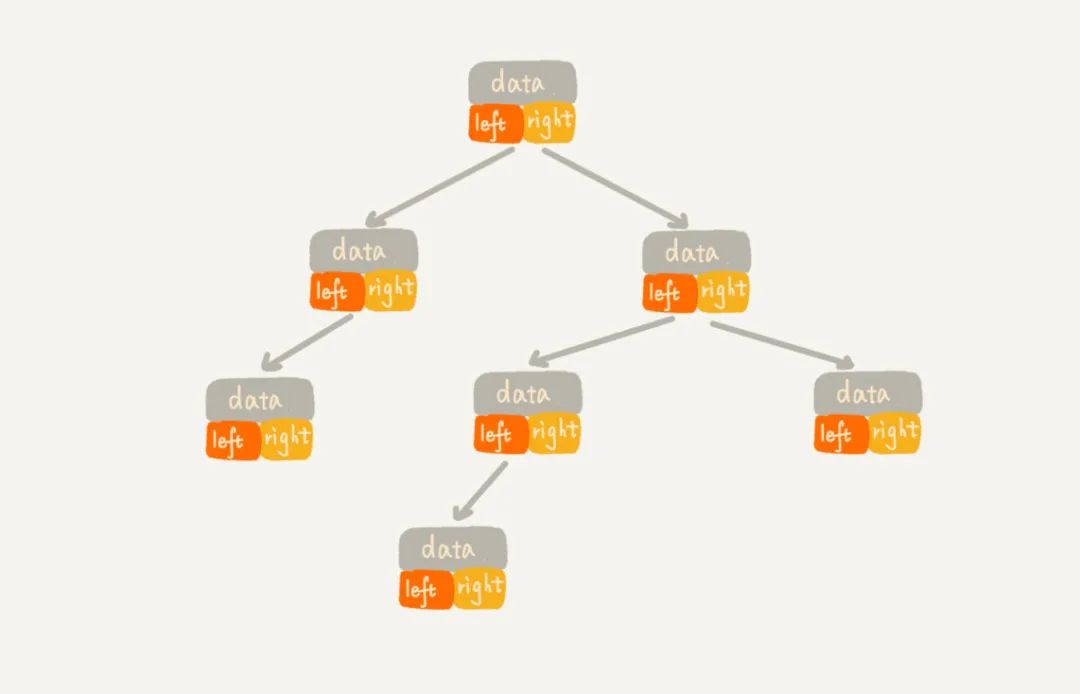
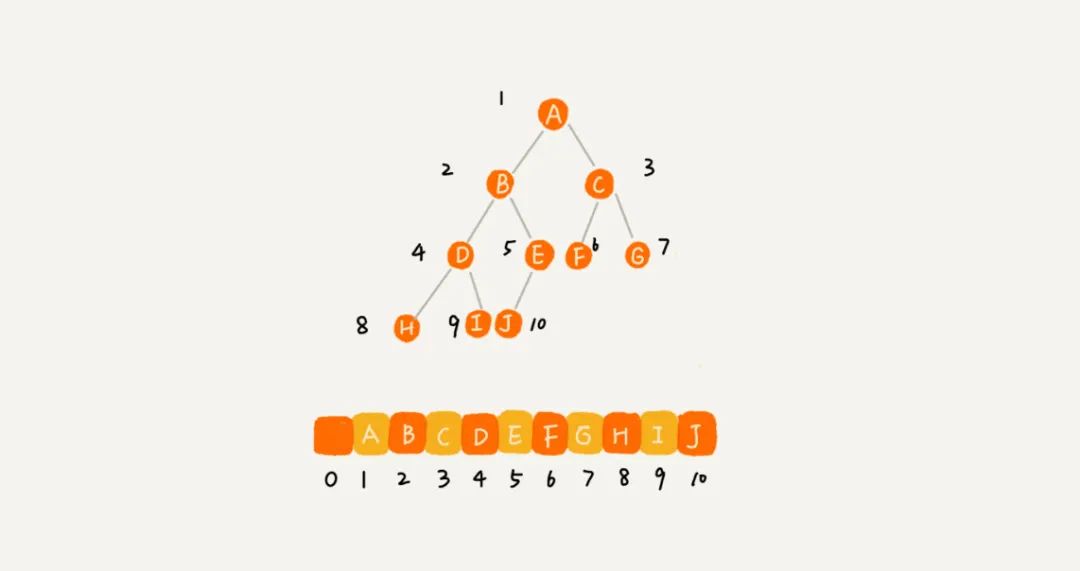
三、二叉树的遍历
前序遍历的递推公式:
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式:
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式:
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print rconst tree = {
value: 1,
left: {
value: 2,
left: {
value: 4
},
right: {
value: 5
}
},
right: {
value: 3,
left: {
value: 6
},
right: {
value: 7
}
}
}
let arrDLR = []
// 前序遍历(根左右)
function DLR(obj) {
arrDLR.push(obj.value)
obj.left && DLR(obj.left)
obj.right && DLR(obj.right)
}
let arrLDR = []
// 中序遍历(左根右)
function LDR(obj) {
obj.left && LDR(obj.left)
arrLDR.push(obj.value)
obj.right && LDR(obj.right)
}
let arrLRD = []
// 后序遍历(左右根)
function LRD(obj) {
obj.left && LRD(obj.left)
obj.right && LRD(obj.right)
arrLRD.push(obj.value)
}
DLR(tree)
console.log(arrDLR) //[ 1, 2, 4, 5, 3, 6, 7 ]
LDR(tree)
console.log(arrLDR) // [ 4, 2, 5, 1, 6, 3, 7 ]
LRD(tree)
console.log(arrLRD) // [ 4, 5, 2, 6, 7, 3, 1 ]以上是关于二叉树(上)的主要内容,如果未能解决你的问题,请参考以下文章