二叉树（下）

Posted 2021-04-23 编程加油站

一、二叉查找树

二叉查找树又叫二叉搜索树，它不仅支持快速查找一个数据，还支持快速插入、删除一个数据。二叉查找树要求，在树中的任意一个节点，它左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值。其结构如下所示：

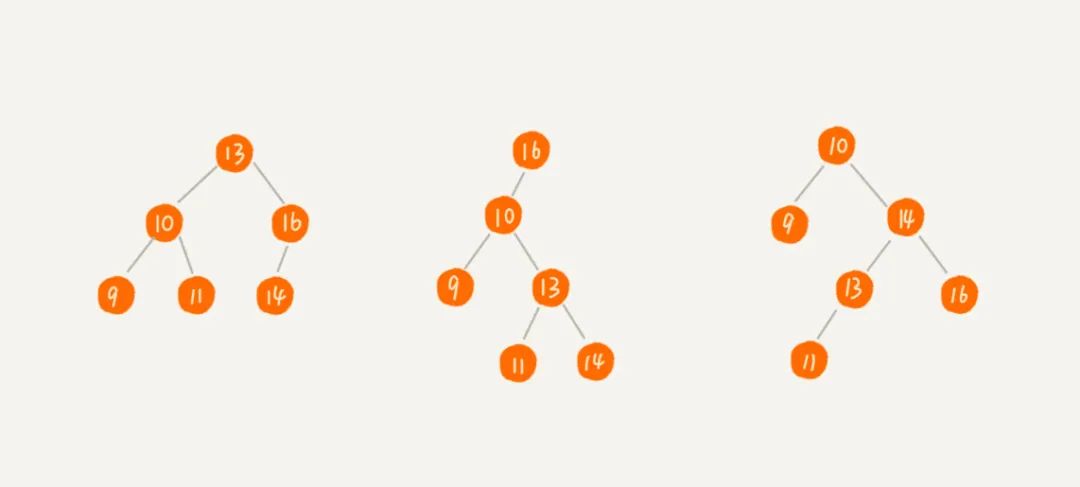
1、二叉查找树的查找操作

查找操作的概括如下：先取根节点，如果它等于我们要查找的数据，那就返回，如果要查找的数据比根节点的值小，那就在左子树中递归查找，如果要查找的数据比根节点的值大，就去右子树中查找。

代码实现如下：

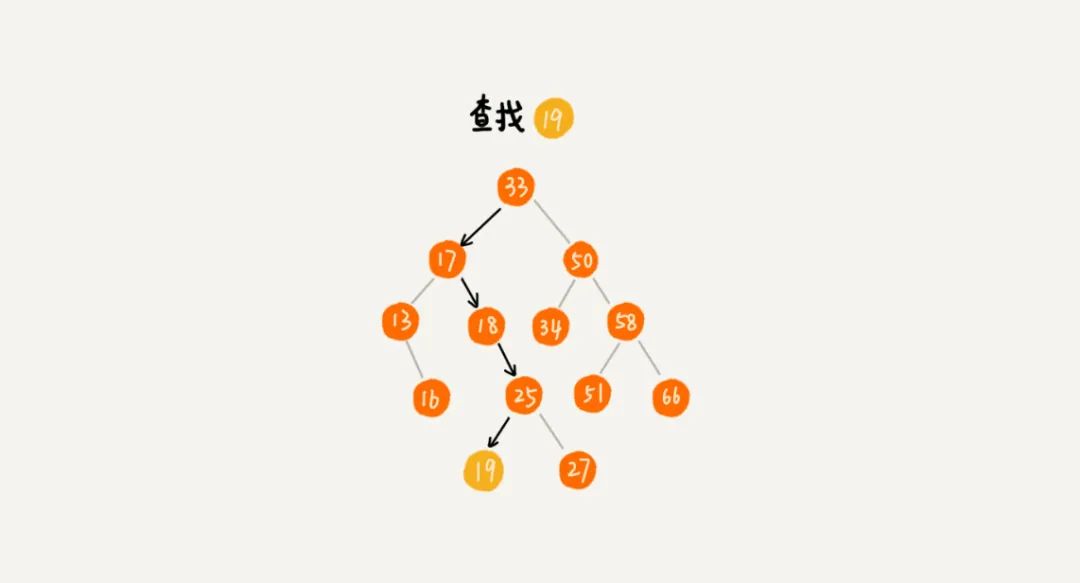
public class BinarySearchTree {
  private Node tree;

  public Node find(int data) {
    Node p = tree;
    while (p != null) {
      if (data < p.data) p = p.left;
      else if (data > p.data) p = p.right;
      else return p;
    }
    return null;
  }

  public static class Node {
    private int data;
    private Node left;
    private Node right;

    public Node(int data) {
      this.data = data;
    }
  }
}

2、二叉树的插入操作

二叉查找树的插入过程与查找类似，新插入的数据一般都是在叶子节点上，我们只需要从根节点开始，依次比较要插入的数据和节点的大小关系。

如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置。如果不为空，就递归遍历右子树，查找插入位置。同样的，如果要插入的数据比节点的数值小，且节点的左子树为空，就将新数据插入到左子节点位置；如果不为空，就再递归遍历左子树，查找插入位置。

插入的代码如下：

public void insert(int data) {
  if (tree == null) {
    tree = new Node(data);
    return;
  }

  Node p = tree;
  while (p != null) {
    if (data > p.data) {
      if (p.right == null) {
        p.right = new Node(data);
        return;
      }
      p = p.right;
    } else { // data < p.data
      if (p.left == null) {
        p.left = new Node(data);
        return;
      }
      p = p.left;
    }
  }
}

3、二叉查找树的删除操作

针对要删除节点的子节点个数不同，分为以下三种情况：

（1）要删除的节点没有子节点：只需要直接将父节点中，指向要删除节点的指针置为null。比如删除图中节点55。

（2）要删除的节点只有一个子节点：只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点即可。比如删除图中节点13。

（3）要删除的节点有两个子节点：首先需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点（因为最小节点肯定没有左子节点，如果有，那就不是最小节点）。比如删除图中节点18。

代码实现如下：

public void delete(int data) {
  Node p = tree; // p指向要删除的节点，初始化指向根节点
  Node pp = null; // pp记录的是p的父节点
  while (p != null && p.data != data) {
    pp = p;
    if (data > p.data) p = p.right;
    else p = p.left;
  }
  if (p == null) return; // 没有找到

  // 要删除的节点有两个子节点
  if (p.left != null && p.right != null) { // 查找右子树中最小节点
    Node minP = p.right;
    Node minPP = p; // minPP表示minP的父节点
    while (minP.left != null) {
      minPP = minP;
      minP = minP.left;
    }
    p.data = minP.data; // 将minP的数据替换到p中
    p = minP; // 下面就变成了删除minP了
    pp = minPP;
  }

  // 删除节点是叶子节点或者仅有一个子节点
  Node child; // p的子节点
  if (p.left != null) child = p.left;
  else if (p.right != null) child = p.right;
  else child = null;

  if (pp == null) tree = child; // 删除的是根节点
  else if (pp.left == p) pp.left = child;
  else pp.right = child;
}

4、二叉树的其他操作

除了插入、删除、查找这个三个操作，二叉查找树中还支持快速的查找最大节点和最小节点、前驱节点和后继节点，完整代码如下：

小tips：中序遍历二叉查找树，可以输出有序的数据序列，时间复杂度为O(n)，因此二叉树也叫做二叉排序树。

class Node {
  constructor(value) {
    this.value = value
    this.left = null
    this.right = null
  }
}

/**
 * 搜索二叉树
 * 允许重复值添加
 */
class SearchTree {
  constructor() {
    this.root = null
  }

  insert(num) {
    let node = new Node(num)
    if (this.root === null) {
      this.root = node
      return
    }
    let prent = this.getPrev(num)
    if (num < prent.value) {
      prent.left = node
    } else {
      prent.right = node
    }

  }

  remove(num) {
    let point = this.root
    let prent = null
    let tree = this

    let res = null
    while (true) {
      if (point.left) {
        if (num < point.left.value || num < point.value) {
          prent = point
          point = point.left
          continue
        }
      }
      if (point.right) {
        if (num >= point.right.value || num >= point.value) {
          if (num === point.value) {
            delMethod(point, prent)
            if (prent === null) {
              point = this.root
            } else {
              prent = prent
              point = prent.right
            }
            res = true
            continue
          }
          prent = point
          point = point.right
          continue
        }
      }
      if (point.value === num) {
        res = true
        delMethod(point, prent)
      }
      break
    }
    return res

    function delMethod(delNode, parent) {
      let p = delNode // p指向要删除的节点
      let pp = parent // pp记录的是p的父节点

      // 要删除的节点有两个子节点
      if (p.left != null && p.right != null) { // 查找右子树中最小节点
        let minP = p.right
        let minPP = p // minPP表示minP的父节点
        while (minP.left != null) {
          minPP = minP
          minP = minP.left
        }
        p.value = minP.value // 将minP的数据替换到p中
        p = minP // 下面就变成了删除minP了
        pp = minPP
      }

      // 删除节点是叶子节点或者仅有一个子节点
      let child // p的子节点
      if (p.left != null) {
        child = p.left
      } else if (p.right != null) {
        child = p.right
      } else {
        child = null
      }

      if (pp == null) {
        tree.root = child
      } else if (pp.left == p) {
        pp.left = child
      } else {
        pp.right = child
      }
    }

  }

  //中序遍历
  print() {
    let point = this.root
    if (point) {
      printAll(point.left)
      console.log(point.value)
      printAll(point.right)
    }

    function printAll(point) {
      if (point == null) {
        return
      }
      printAll(point.left)
      console.log(point.value)
      printAll(point.right)
    }
  }

  find(num) {
    if (this.root === null) {
      return
    }
    return this.getPrev(num, true)
  }

  //添加和查找的公用部分
  getPrev(num, find = false) {
    let point = this.root
    let res = []
    while (true) {
      if (point.left) {
        if (num < point.left.value || num < point.value) {
          point = point.left
          continue
        }
      }

      if (point.right) {
        if (num >= point.right.value || num >= point.value) {
          //搜索时如果有多个值则缓存
          if (find && num === point.value) {
            res.push(point.value)
          }
          point = point.right
          continue
        }
      }
      //如果是搜索
      if (find) {
        if (point.value === num) {
          res.push(point.value)
        }

        if (res.length === 0) {
          return null
        }

        if (res.length === 1) {
          return res[0]
        }

        return res
      }
      //如果是添加 返回的是应该添加的那各节点的父节点
      return point
    }
  }
}


//测试
function doTest() {
  let searchTree = new SearchTree()
  console.log('新增 4 1 2 5 四个元素')
  searchTree.insert(4)
  searchTree.insert(1)
  searchTree.insert(2)
  searchTree.insert(5)
  console.log('新增 4 1 2 5 四个元素后，中序遍历结果如下：')
  searchTree.print() //1 2 4 5

  console.log('删除元素1')
  searchTree.remove(1)
  console.log('删除元素1后结果如下：')
  searchTree.print() // 2 4 5

  console.log('删除元素4')
  searchTree.remove(4)
  console.log('删除元素4后结果如下：')
  searchTree.print() // 2 5

  console.log('插入元素 3 7 1 5 5 5')
  searchTree.insert(3)
  searchTree.insert(7)
  searchTree.insert(1)
  searchTree.insert(5)
  searchTree.insert(5)
  searchTree.insert(5)
  console.log('插入元素 3 7 1 5 5 5后结果如下：')
  searchTree.print()// 1 2 3 5 5 5 5 7

  console.log('打印查找5')
  console.log(searchTree.find(5))// [5,5,5,5]

  console.log('移除元素5')
  searchTree.remove(5)
  console.log('移除元素5结果如下：')
  searchTree.print()// 1 2 3 7

  console.log('打印查找2')
  console.log(searchTree.find(2))

  console.log('打印查找30')
  console.log(searchTree.find(30))
}

doTest()

二、二叉查找树的时间复杂度分析

通过前面的了解，不论是插入、删除还是查找，二叉查找树的时间复杂度都跟树的高度成正比，可以暂时表示为O(height)，假设一棵完全二叉树包含n个节点，如何求他的高度呢？

包含n个节点的完全二叉树，第一层包含1个节点，第二层包含2个节点，第三层包含4个节点，以此类推，下一层的节点是上一层节点的2倍，则第k层有2^（k-1）个节点，对于完全二叉树来说，最后一层不一定是满的，最后一层的节点在1 — 2^（k-1）之间，如果节点个数是n，那么n满足的关系如下：

n >= 1+2+4+8+...+2^(k-2)+1
n <= 1+2+4+8+...+2^(k-2)+2^(k-1)

依据等比数列求和公式，可以计算出k 的范围是[log2(n+1), log2(n) +1]。树的层数小于等于log2(n) +1，树的高度等于最大层数-1，所以完全二叉树的高度小于等于log2(n)。