遍历二叉树的递归与非递归代码实现

Posted 2021-04-23 嵌入式那点事儿

遍历二叉树可以用递归的方法去实现，也可以用非递归的方法去实现。递归代码的好处是简洁，直观，最主要的还是递归的代码少，很快就可以写完。但我们知道，递归的调用会用到一个专门的栈，这个栈的深度是有限的，如果递归函数调用的次数很多，超过栈限制的深度，那么程序就会崩溃。这个时候就需要把递归的代码改为非递归了。因此，了解掌握遍历二叉树的非递归实现还是很有必要的。

下面会给出先序遍历，中序遍历，后序遍历的递归与非递归代码，以及层次遍历的代码。

首先，先给出二叉树的节点定义：

1 struct BinTNode {
2     int data;
3     BinTNode *lchild, *rchild;
4 };

先序遍历

先序遍历，就是先访问根节点，再访问左子树，最后再访问右子树。而要访问左子树，同样是先访问左子树的根节点，再访问左子树的左子树，最后再访问左子树的右子树。访问右子树也是同样的方法。所以，我们自然而然想到用递归的算法。

为了方便表述，我们遍历二叉树所做的事情是把该节点的值输出。

对于一个递归函数，我们不应该跳到递归里面去，而是去理解递归函数的定义，也就是它的作用是什么？递归结束后会返回什么样的结果？

　　我们把先序遍历的递归函数定义为：传入一个根节点，如果这个节点不为空，就输出根节点的值，然后把左子树的所有节点的值输出，再把右子树的所有节点的值输出，这就是先序遍历递归函数的作用。由于函数的返回值是void，所有递归结束后不会有返回结果。所以再按照先序遍历的定义，我们可以把递归函数写成下面这样：

1 void preOrderTraversal(BinTNode *T) {
2     if (T) {                            // 节点不为空才可以输出值 
3         cout << T -> data;              // 先输出根节点的值 
4         preOrderTraversal(T -> lchild); // 再把左子树的根，也就是T -> lchild传到我们的递归函数中，输出左子树所有节点的值 
5         preOrderTraversal(T -> rchild); // 最后把右子树的根，也就是T -> rchild传到我们的递归函数中，输出右子树所有节点的值 
6     }
7 }

了解了递归的代码后，接下来就是先序遍历的非递归实现。

我们知道，当调用递归函数来遍历二叉树，每一个节点都会被访问3次。

而先序遍历就对应着当该节点被第1次访问时就，输出该节点的值。由于递归的本质是运用栈，因此我们也可以模拟一个栈来实现非递归。当遇到一个不为空的节点时，我们把这个节点压入栈，这就对应于第1次访问这个节点，所以在压入栈后，输出该节点的值。然后一直做T = T -> lchild这个动作，把节点对应的左子树节点压到栈，同时输出节点的值。直到左子树为空，这时就弹出栈顶元素，这个时候该节点被第2次访问。把弹出节点的右子树节点再压入栈中。这个过程不断重复，直到节点和栈都为空。这就实现了先序遍历，先是根节点，再是左子树，最后是右子树。

　　先序遍历的非递归代码如下：

 1 void preOrderTraversal(BinTNode *T) {
 2     SNode *S = initStack();     // 申请一个栈
 3     while (T || !isEmpty(S)) {  // 循环的条件是根节点和栈不同时为空 
 4         if (T) {                // 如果根节点存在不为空 
 5             push(S, T);         // 把根节点压入栈 
 6             cout << T -> data;  // 由于是第一次访问该节点，所以输出节点的值 
 7             T  = T -> lchild;   // 把左子树的根节点赋值给T，进入下一次循环 
 8         }
 9         else {                  // 如果根节点为空 
10             T = pop(S);         // 弹出栈顶元素，第二次访问该节点  
11             T = T -> rchild;    // 把右子树的根节点赋值给T，进入下一次循环
12         }
13     }
14 }

还有另外一种先序遍历的非递归代码，和上面的代码几乎一样：

 1 void preOrderTraversal(BinTNode *T) {
 2     SNode *S = initStack();
 3     while (T || !isEmpty(S)) {
 4         while (T) {
 5             push(S, T);
 6             cout << T -> data;
 7             T = T -> lchild;
 8         }
 9         if (!isEmpty(S)) {
10             T = pop(S);
11             T = T -> rchild;
12         }
13     }
14 }

中序遍历

中序遍历，就是先访问左子树，再访问根节点，最后再访问右子树。而要访问左子树，同样是先访问左子树的左子树，再访问左子树的根节点，最后再访问左子树的右子树。访问右子树也是同样的方法。所以，同样可以用递归去实现。

我们把中序遍历的递归函数定义为：传入一个根节点，如果这个节点不为空，先把左子树的所有节点的值输出，再输出根节点的值，最后把右子树的所有节点的值输出。其实，按照中序遍历的定义，把先序遍历的部分递归代码进行交换，就变成中序遍历了：

1 void inOrderTraversal(BinTNode *T) {
2     if (T) {                            // 节点不为空才可以输出值
3         inOrderTraversal(T -> lchild);  // 先把左子树的根，也就是T -> lchild传到我们的递归函数中，输出左子树所有节点的值
4         cout << T -> data;              // 再输出根节点的值
5         inOrderTraversal(T -> rchild);  // 最后把右子树的根，也就是T -> rchild传到我们的递归函数中，输出右子树所有节点的值
6     }
7 }

接下来是中序遍历的非递归实现。按中序遍历的定义，当节点被第2次访问时，我们就输出节点的值。所以中序遍历和先序遍历的非递归实现几乎一样，只不过是在节点被第2次访问时才输出该节点的值，所以我们只需要把输出语句改放到该节点被第2次访问之后就可以了，也就是改放到节点从栈顶被弹出之后。

 1 void inOrderTraversal(BinTNode *T) {
 2     SNode *S = initStack();
 3     while (T || !isEmpty(S)) {
 4         if (T) {
 5             push(S, T);         // 把根节点压入栈，第一次访问该节点 
 6             T  = T -> lchild;
 7         }
 8         else {
 9             T = pop(S);         // 弹出栈顶元素，第二次访问该节点 
10             cout << T -> data;  // 由于是第二次访问该节点，所以输出节点的值 
11             T = T -> rchild;
12         }
13     }
14 }

还有另外一种中序遍历的非递归代码，和上面的代码几乎一样：

 1 void inOrderTraversal(BinTNode *T) {
 2     SNode *S = initStack();
 3     while (T || !isEmpty(S)) {
 4         while (T) {
 5             push(S, T);
 6             T = T -> lchild;
 7         }
 8         if (!isEmpty(S)) {
 9             T = pop(S);
10             cout << T -> data;
11             T = T -> rchild;
12         }
13     }
14 }

后序遍历

后序遍历，就是先访问左子树，再访问右子树，最后再访问根节点。而要访问左子树，同样是先访问左子树的左子树，再访问左子树的右子树，最后再访问左子树的根节点。访问右子树也是同样的方法。所以，同样可以用递归去实现。

我们把后序遍历的递归函数定义为：传入一个根节点，如果这个节点不为空，先把左子树的所有节点的值输出，再把右子树的所有节点的值输出，最后再输出根节点的值。和上面一样，后序遍历的递归函数只需要把部分递归代码进行交换：

1 void postOrderTraversal(BinTNode *T) {
2     if (T) {                              // 节点不为空才可以输出值 
3         postOrderTraversal(T -> lchild);  // 先把左子树的根，也就是T -> lchild传到我们的递归函数中，输出左子树所有节点的值
4         postOrderTraversal(T -> rchild);  // 再把右子树的根，也就是T -> rchild传到我们的递归函数中，输出右子树所有节点的值
5         cout << T -> data;                // 最后输出根节点的值
6     }
7 }

至于后序遍历的非递归实现，就没有那么容易了。如果我们尝试在前面的先序遍历和中序遍历的非递归代码中，调换cout << T -> data; 这条语句的位置，我们会发现无论我们把它放在哪里，都无法实现后续遍历。这是由于在先序遍历和中序遍历的非递归代码中，每个节点最多能被访问2次，也就是在压入和弹出时被访问。而后序遍历要求是在节点被第3次访问时才输出节点的值。所以很明显，之前的非递归函数并不能够实现后序遍历。所以我们只能够用其他的方法来实现非递归的后序遍历。

下面给出两种不同的后序遍历的非递归代码实现：

1. 在节点中加入一个标志域。

1 struct BinTNode {
2     int data;
3     BinTNode *lchild, *rchild;
4     bool isFirst;    // 第一次访问节点时赋值为true；第二次访问时，也就是从栈顶弹出时赋值为false，再压入栈中；当节点再弹出时已是第三次访问该节点了 
5 };

标志域的作用就是，当节点是第一次被弹出时，如果节点的标志域为true，那么我们再次把它压入栈里面，同时把标志域改为false，这样该节点就可以再弹出一次。当再次弹出该节点时，又因为此时节点的标志域为false，不会再被压入，从而该节点就可以实现被访问3次了。

这样子我们就可以对一个节点访问3次，在第3次访问时输出该节点的值，从而就可以实现后序遍历了：

 1 void postOrderTraversal(BinTNode *T) {
 2     SNode *S = initStack();
 3     while (T || !isEmpty(S)) {
 4         if (T) {
 5             push(S, T);                  // 把根节点压入栈，第一次访问该节点
 6             T -> isFirst = true;         // 标志域赋值为true 
 7             T = T -> lchild;
 8         }
 9         else {
10             T = pop(S);
11             if (T -> isFirst) {         // 如果节点的标志域为true 
12                 push(S, T);             // 我们继续把它压入栈中，同时该节点被第二次访问 
13                 T -> isFirst = false;   // 同时再为该节点的标志域赋值为false，下一次再弹出该节点时就不再压入栈中 
14                 T = T -> rchild;
15             }
16             else {                      // 如果节点的标志域为false 
17                 cout << T -> data;      // 此时是第三次访问该节点，可以输出该节点的值了 
18                 T = NULL;               // 该节点的左右孩子都访问完了，我们把NULL赋值给T，在下一次的循环，去接收栈顶元素 
19             }
20         }
21     }
22 }

2. 借助辅助指针last，last指向最近访问过的节点，也就是指向从栈顶弹出后，没有再被压入栈的那个节点。

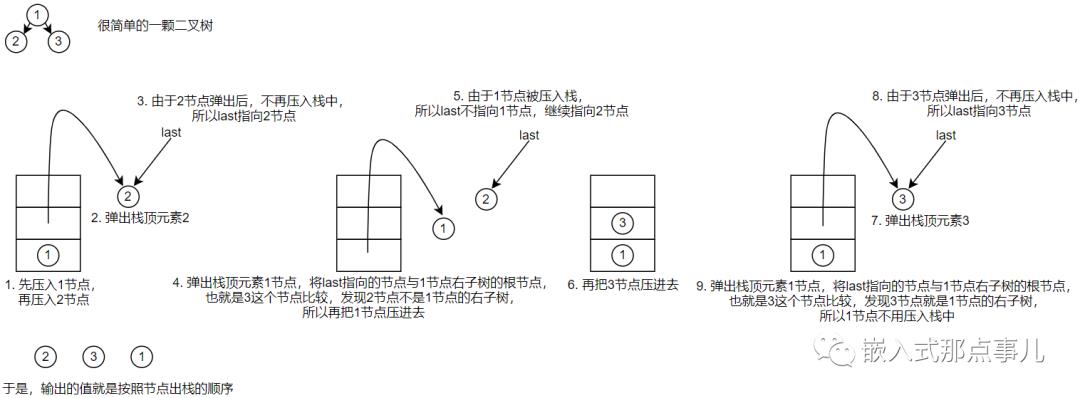
用栈来存储节点时，按照先序遍历和中序遍历的非递归代码，节点只能被访问两次。而后序遍历的顺序是先访问左子树，再访问右子树，最后才访问根节点。所以我们应该分清除当一个根节点从栈顶弹出时，上一次从栈顶弹出的节点到底是它的左子树的根节点，还从它右子树的根节点。所以，可以用辅助指针last，来指向最近访问过的节点，看它是不是该节点右子树的根节点。如果是，就说明该节点的左右子树都已经访问完了，可以输出该节点的值了。

举个简单的例子：

 1 void postOrderTraversal(BinTNode *T) {
 2     SNode *S = initStack();
 3     BinTNode *last = NULL;                                // last指向刚访问完的节点    
 4     while (T || !isEmpty(S)) {
 5         if (T) {
 6             push(S, T);
 7             T = T -> left;
 8         }
 9         else {
10             T = pop(S);
11             if (T -> rchild && T -> rchild != last) {    // 如果该根节点的右孩子不为空，并且该根节点的右孩子不是刚访问的那个节点（这意味着该根节点的右子树还没有访问，是从左子树返回到该根节点的）
12                 push(S, T);                              // 再把该根节点压入，这样子当该节点再次被弹出时，已是被第三次访问了 
13                 T = T -> rchild;                         // 向下一次循环传入该根节点右子树的根节点 
14             }
15             else {                                       // 根节点的右孩子为空或者该根节点的右孩子就是刚访问的那个节点（这意味着该根节点的右子树已经被访问了，是从右子树返回到该根节点的）
16                 cout << T -> data;                       // 第三次访问该节点，所以输出节点的值
17                 last = T;                                // 因为该根节点被访问了，所以last指向该节点 
18                 T = NULL;                                // 由于该节点的左右孩子都访问完了，我们把NULL赋值给T，在下一次的循环，去接收栈顶元素 
19             }
20         }
21     }
22 }

层次遍历

最后一个是层次遍历，它不是用栈来实现的，而是用队列来实现的。类似于图的广度优先搜索（BFS）。

因此，如果要用递归来实现层次遍历，这会是很困难的事情。这里就不讨论了。

下面给出层次遍历的代码：

 1 void levelOrderTraversal(BinTNode *T) {
 2     if (T == NULL) return;
 3     
 4     QNode *Q = initQueue();
 5     push(Q, T);
 6     while (!isEmpty(Q)) {
 7         T = pop(S);
 8         cout << T -> data;
 9         
10         if (T -> lchild) push(Q, T -> lchild);
11         if (T -> rchild) push(Q, T -> rchild);
12     }
13 }

Stay hungry，Stay Foolish。

求知若饥，虚心若愚