是什么让普通的链表也能达到二分查找的效率?没错,就是跳表
Posted 程序猿秘籍
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了是什么让普通的链表也能达到二分查找的效率?没错,就是跳表相关的知识,希望对你有一定的参考价值。
继承,是幸福的延续;重载,是幸福的重生。
数组与链表
数组
优点
随机访问速度较快(基于下标访问)。
实现简单,使用简单。
缺点
内存连续可以是优点,也可以是缺点,如果在内存紧张的情况下,数组将会被大大限制。
插入和删除的时候会导致元素的移动(数据拷贝),较慢。
数组大小固定,大大的限制了元素的个数,对于很多动态的数据不友好。
链表
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间。
优点
链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。
删除插入不用移动其他元素。
不受元素大小限制,可以随意扩展。
缺点
失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
随机访问效率相对数组来说较低。
时间复杂度分析
随机访问
数组:O(1)不支持随机访问插入,删除 数组:有序数组 ->O(n),无序数组 ->(1) 链表:O(1) 链表又可以分为单链表和双向链表,不过这都不是这篇文章需要讨论的问题,这里讲一下数组和链表,只是做一下铺垫,因为下面讲到的跳表就会用到链表的相关知识,所以对链表还不怎么熟悉的同学,可以先学习一下,然后在开始今天的正文:跳表。
什么是跳表?
上文讲到了链表的概念,链表的查询时间复杂度为:O(n),即使是有序的链表,也得从链表的第一个元素开始遍历查找,时间复杂度偏高,那如果让你来优化,你有什么解决方案吗?这个时候跳表就出现了。
跳表,全称:跳跃链表,在计算机科学中,跳跃列表是一种数据结构。它使得包含n个元素的有序序列的查找和插入操作的平均时间复杂度都是:logn, 我们来画一个普通的链表结构
这是一个普通的单链表结构,如果我们想查找出 58 这个节点,我们就得查询 1 -> 4 -> 7 -> 15 -> 20 -> 35 -> 50 -> 58 ,一共查找了8次,才将我们需要的结果查找出来,时间复杂度:O(n),效率可想而知,那我们一起试着来优化一下。
mysql在数据量大的时候查询效率也会急剧下降,他们是怎么来优化效率问题呢?那就是索引,这里我们也可以使用一个类似 “索引” 的东西来对这个普通的单链表进行优化。
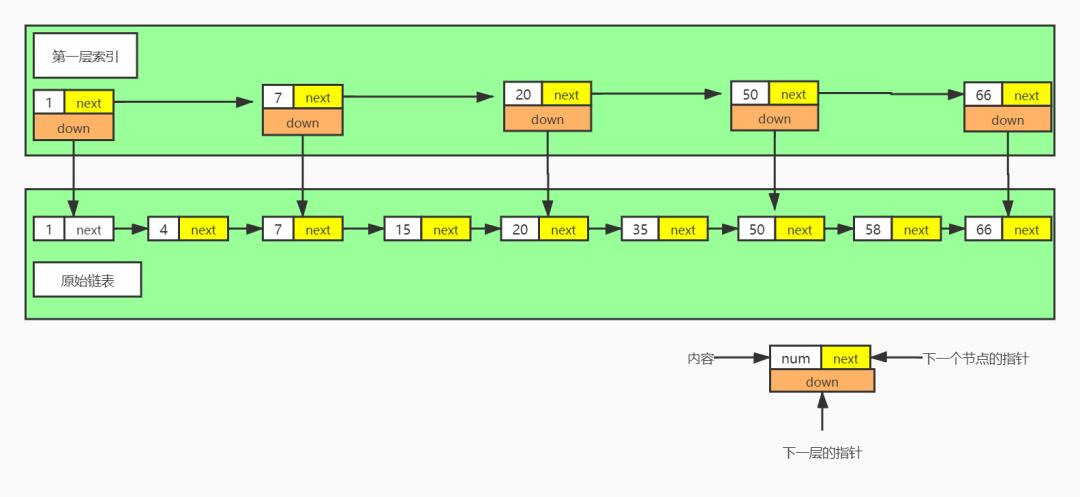
我们将原始链表中每隔两个结点之后的节点复制一份出来,用于制作索引,方便数据的查找。
我们还是继续查找58,我们只需要经过:1 -> 7 -> 20 --> 50 -> 58,发现了没有,这里居然只搜索了5次就找到了我们想要的结点,效率是不是提升了一丢丢?我现在来解释一下这张图,由于我们建立了一层索引,所以查询的时候优先往第一层索引层搜索,搜索索引层时,发现 50 以及之前的节点都小于 58 ,遍历到 50 的时候,他的下一个节点 66 大于需要查询的节点 ,所以这个时候就会找到50这个节点中的down(原始链表节点为 50 的指针)节点,然后再往下遍历一个就就找到了 58 。
加了“索引” 也才少查询了三次,优化的并不是很明显啊,这个优化是否有存在的必要呢?我们这里只建立了一层“索引”,我们多建立几层”索引“之后呢?会是什么样呢?
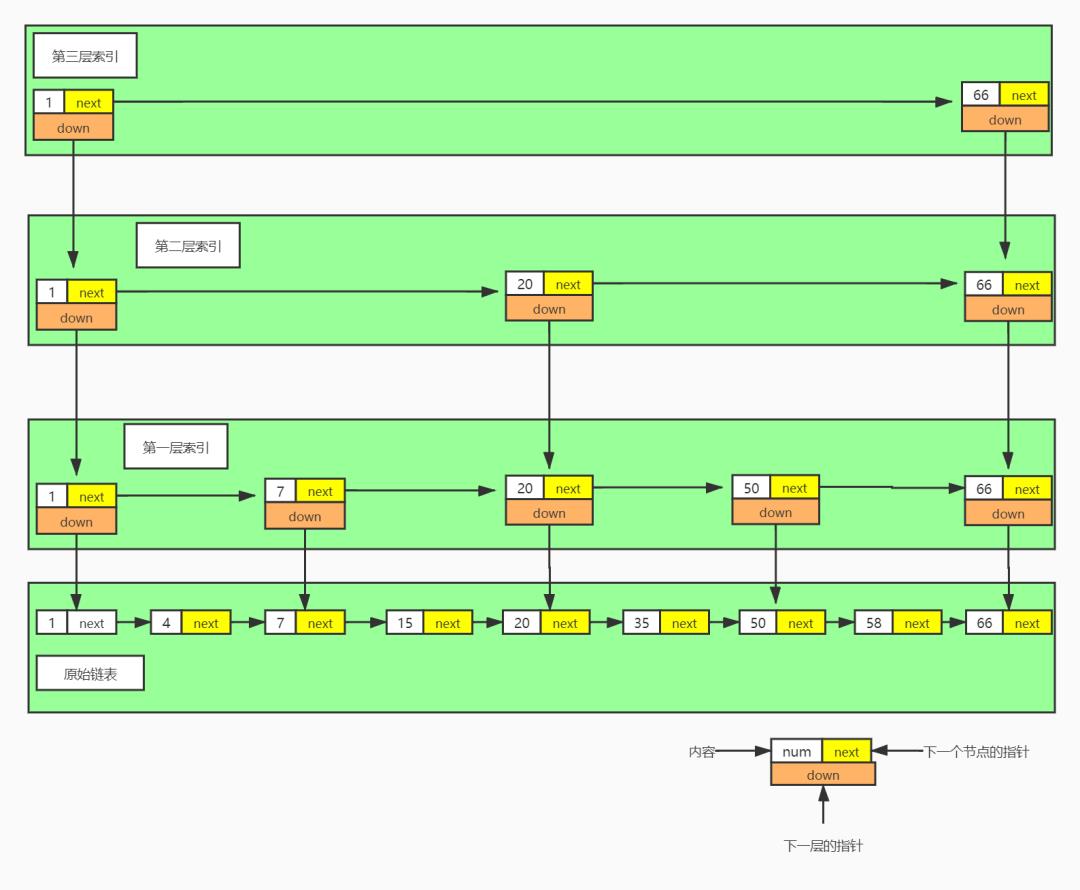
这个时候我们发现只需要4次就能找到我们需要查找的节点 58 ,4 次相对于8次来说已经快了一半了,我这里的数据不是太多,当数据足够多的时候,效果将会更为明显。
这种一层一层的索引组成的数据结构,我们称他为:跳表,现在相信你对什么是跳表应该有了比较深的理解了吧,这个时候你可能又有一个疑问了?我们为了建立索引层,肯定会消耗大量的空间,这是属于空间换时间的一种方式,但是在数据量大的时候,会不会存在空间不够的情况呢?
那我们现在一起来分析一下跳表的时间/空间复杂度吧
跳表分析
假设原始链表结点个数为:n,我们知道,我们每隔两个节点抽离一个结点作为索引层的一个结点,那么第一层索引层的结点个数应该是原始链表结点个数的1/2,也就是n/2,第二层索引的结点个数是第一层索引结点个数的1/2,是 1/4 原始链表结点个数,也就是 n/4,第三层索引的结点个数是第二层结点个数的1/2,是第一层索引结点个数的4/1,是原始链表结点个数的1/8,依次类推,在k层索引的节点个数是k-1层索引的1/2,那么k层索引的节点个数:
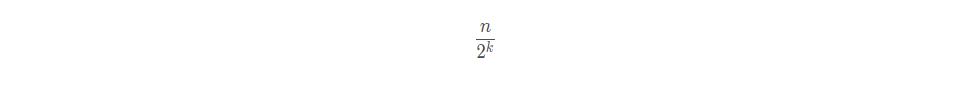
一个链表,假设我们都是每隔两个结点分配一个索引结点,最高层索引只有两个结点,索引层高度为:h,那么将会得到这么一个公式:
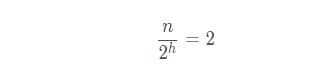
我们求解一下 h:
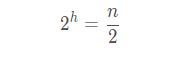
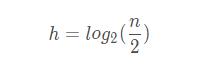
我们将这个公式拆分一下:
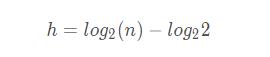
所以 h 的值为:
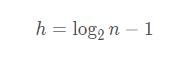
由于 h 是索引层的高度,我们算上原始链表,那么整个跳表的高度就是:
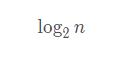
现在我们一起来算算跳表查询的时间复杂度,跳表有许多层索引,每层索引都会进行相对应次数的遍历,假设每次索引遍历的最大次数为:x,那么一个查询需要遍历的次数为:

所以用 O 表示法表示,跳表的时间复杂度为:
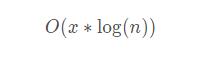
为什么对数中的底数 2 没有了呢?其实在时间复杂度分析中,分析的只是一种趋势,并不是固定的值,相对数级别的,底数可以忽略,具体相关的介绍,这里就不展开介绍了,感兴趣的可以百度一下,并不复杂,我们现在需要搞明白的是这个 x 到底是多少呢?
在前面所画的跳表结构图中,我们以每隔两个结点提取一个索引结点,所以,当我们需要查询跳表中某一个结点时,需要在索引层从上而下开始遍历,每层最多不会超过3个,为什么是 3 个而不是 4 个、5 个、6 个呢?我们画一个简单的图来说明一下。
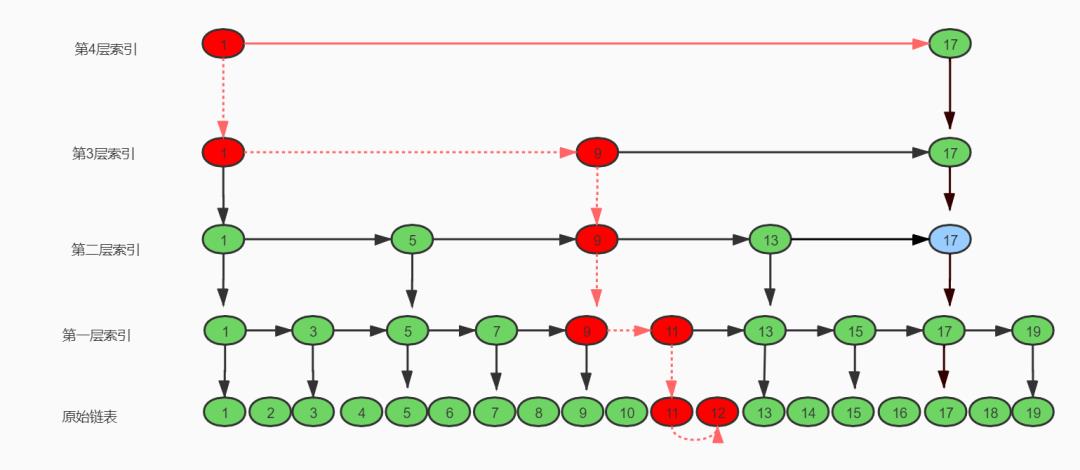
我们需要查找 12 这个结点,当走到 9 这个结点时发现 12 > 9 而 < 13 所以下降一层索引,到达第一层索引,而在 9 - 13 之间只有三个结点,就算是下降到原始链表也是一样的,两个范围结点之前最多只有三个结点,所以 每层需要遍历的最多结点数就是这么得出来的,因为 x 是常数 3 ,可以直接省略,所以跳表最终的时间复杂度为:
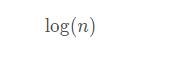
虽然查询的效率提高了非常多,但是这也存在一个非常重要的问题,那就是跳表会占用额外的内存空间,因为,它需要很多层的索引,这样这个数据结构还值不值得推荐使用呢?既然redis官方都在使用了,你还在怕什么呢?我们再来分析一下跳表的空间复杂度,看看是不是对内存有着极大的消耗呢?
假设原始链表长度为 n ,那么第一层索引长度为 n/2,第二层索引长度为:n/4,第三层索引长度:n/8,最后一层(最高层)索引长度:2,很明显这是一个等比数列:
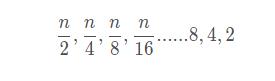
等比数列求和公式:
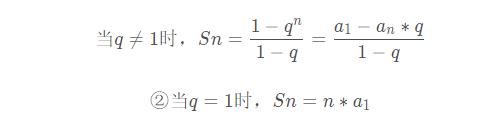
套入公式:
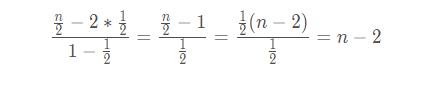
索引层占用总大小为:n - 2,加上原始链表 n = 2n -2 ,所以跳表的空间复杂度为:O(n),常数可以省略,这是每个两个结点提取一个索引结点的空间复杂度,那多隔几个结点提取一个索引结点呢?比如每隔 3 个提取一个,每隔 5 个提取一个,计算方式和上面一样,结果空间复杂度也是:O(n),但是空间确实减少了很多。
查询我们讲完了,那跳表的插入和删除效果怎么样呢?会不会也表现得很优秀?我们一起来看看。
由于我们的链表是有序的,所以在插入的时候我们得先找到插入的位置,跳表的查询时间复杂度为O(logn ),找到了需要插入的位置之后就是插入操作,单链表的插入时间复杂度是O(1),这里就不证明了,所以整个插入的过程等于查找插入的位置+插入=O(logn)。
其实删除操作的时间复杂也是O(logn),为什么呢?其实和插入也是一样的,但是会多一个查找前驱结点的操作,因为删除,会导致前后驱结点的指针变动,后驱结点在当前删除的结点中存在,但是前前驱节点没有,查询也是O(logn),所以删除 O(logn)+O(logn),所以删除的时间复杂度最终还是:O(logn),但是删除有一点需要注意,如果需要删除的结点在索引层也存在,那么同时需要删除索引层的结点,关于前驱结点的问题,可以使用双向链表解决。
索引更新
跳表的查询、删除、添加在性能方面都比较优秀,那它能一直保持这么优秀吗?既然跳表也是用来存放数据的,那么肯定会伴随着频繁的新增和删除,假设在某一个相邻区间的索引结点之间被插入了较多的数据,那么就会导致数据分布不均匀,在某一个区间的查询时间效率降低,最坏情况可能会被退化成单链表,所有的数据都在这一个区间内,所以我们在数据插入的时候对索引层做实时更新维护,保证跳表的数据结构不会过度退化,那我们怎么维护索引层的变化呢?
其实也不难,跳表通过随机函数来保持数据的平衡性,也就是让数据保持相对均匀,当我们往跳表中添加数据的时候,通过随机函数生成一个随机数,这个随机数就是索引的层数,然后在这一层把需要添加的结点添加到这一层索引层节点中,假设我们需要插入的数据为 7 ,随机函数生成的随机数为:2,那么插入的时候就会如下图所示:
这里就对随机函数的要求很高了,它可以很好地保证跳表的平衡性,不会让跳表的性能退化,这点和红黑树的左旋/右旋是一个道理。
代码实现
上面的都是理论基础,我们看完了理论,那一定要真刀真枪地干一下,不然不就白看了吗,那我们一起来看看跳表的代码如何实现
``
package com.lx.cloud.test;
import java.util.Random;
/**
* @ClassName SkipList
* @Description 跳表
*/
public class SkipList {
private static final int MAX_LEVEL = 16;
private int levelCount = 1;
/**
* 带头链表
*/
private Node head = new Node(MAX_LEVEL);
private Random r = new Random();
public Node find(int value) {
Node p = head;
// 从最大层开始查找,找到前一节点,通过--i,移动到下层再开始查找
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
// 找到前一节点
p = p.forwards[i];
}
}
if (p.forwards[0] != null && p.forwards[0].data == value) {
return p.forwards[0];
} else {
return null;
}
}
/**
* 优化了作者zheng的插入方法
*
* @param value 值
*/
public void insert(int value) {
int level = head.forwards[0] == null ? 1 : randomLevel();
// 每次只增加一层,如果条件满足
if (level > levelCount) {
level = ++levelCount;
}
Node newNode = new Node(level);
newNode.data = value;
Node update[] = new Node[level];
for (int i = 0; i < level; ++i) {
update[i] = head;
}
Node p = head;
// 从最大层开始查找,找到前一节点,通过--i,移动到下层再开始查找
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
// 找到前一节点
p = p.forwards[i];
}
// levelCount 会 > level,所以加上判断
if (level > i) {
update[i] = p;
}
}
for (int i = 0; i < level; ++i) {
newNode.forwards[i] = update[i].forwards[i];
update[i].forwards[i] = newNode;
}
}
/**
* 优化了作者zheng的插入方法2
*
* @param value 值
*/
public void insert2(int value) {
int level = head.forwards[0] == null ? 1 : randomLevel();
// 每次只增加一层,如果条件满足
if (level > levelCount) {
level = ++levelCount;
}
Node newNode = new Node(level);
newNode.data = value;
Node p = head;
// 从最大层开始查找,找到前一节点,通过--i,移动到下层再开始查找
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
// 找到前一节点
p = p.forwards[i];
}
// levelCount 会 > level,所以加上判断
if (level > i) {
if (p.forwards[i] == null) {
p.forwards[i] = newNode;
} else {
Node next = p.forwards[i];
p.forwards[i] = newNode;
newNode.forwards[i] = next;
}
}
}
}
/**
* 作者zheng的插入方法,未优化前,优化后参见上面insert()
*
* @param value
* @param level 0 表示随机层数,不为0,表示指定层数,指定层数
* 可以让每次打印结果不变动,这里是为了便于学习理解
*/
public void insert(int value, int level) {
// 随机一个层数
if (level == 0) {
level = randomLevel();
}
// 创建新节点
Node newNode = new Node(level);
newNode.data = value;
// 表示从最大层到低层,都要有节点数据
newNode.maxLevel = level;
// 记录要更新的层数,表示新节点要更新到哪几层
Node update[] = new Node[level];
for (int i = 0; i < level; ++i) {
update[i] = head;
}
/**
*
* 1,说明:层是从下到上的,这里最下层编号是0,最上层编号是15
* 2,这里没有从已有数据最大层(编号最大)开始找,(而是随机层的最大层)导致有些问题。
* 如果数据量为1亿,随机level=1 ,那么插入时间复杂度为O(n)
*/
Node p = head;
for (int i = level - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
p = p.forwards[i];
}
// 这里update[i]表示当前层节点的前一节点,因为要找到前一节点,才好插入数据
update[i] = p;
}
// 将每一层节点和后面节点关联
for (int i = 0; i < level; ++i) {
// 记录当前层节点后面节点指针
newNode.forwards[i] = update[i].forwards[i];
// 前一个节点的指针,指向当前节点
update[i].forwards[i] = newNode;
}
// 更新层高
if (levelCount < level){
levelCount = level;
}
}
public void delete(int value) {
Node[] update = new Node[levelCount];
Node p = head;
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
p = p.forwards[i];
}
update[i] = p;
}
if (p.forwards[0] != null && p.forwards[0].data == value) {
for (int i = levelCount - 1; i >= 0; --i) {
if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
update[i].forwards[i] = update[i].forwards[i].forwards[i];
}
}
}
}
/**
* 随机 level 次,如果是奇数层数 +1,防止伪随机
*
* @return
*/
private int randomLevel() {
int level = 1;
for (int i = 1; i < MAX_LEVEL; ++i) {
if (r.nextInt() % 2 == 1) {
level++;
}
}
return level;
}
/**
* 打印每个节点数据和最大层数
*/
public void printAll() {
Node p = head;
while (p.forwards[0] != null) {
System.out.print(p.forwards[0] + " ");
p = p.forwards[0];
}
System.out.println();
}
/**
* 打印所有数据
*/
public void printAll_beautiful() {
Node p = head;
Node[] c = p.forwards;
Node[] d = c;
int maxLevel = c.length;
for (int i = maxLevel - 1; i >= 0; i--) {
do {
System.out.print((d[i] != null ? d[i].data : null) + ":" + i + "-------");
} while (d[i] != null && (d = d[i].forwards)[i] != null);
System.out.println();
d = c;
}
}
/**
* 跳表的节点,每个节点记录了当前节点数据和所在层数数据
*/
public class Node {
private int data = -1;
/**
* 表示当前节点位置的下一个节点所有层的数据,从上层切换到下层,就是数组下标-1,
* forwards[3]表示当前节点在第三层的下一个节点。
*/
private Node forwards[];
/**
* 这个值其实可以不用,看优化insert()
*/
private int maxLevel = 0;
public Node(int level) {
forwards = new Node[level];
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
builder.append("{ data: ");
builder.append(data);
builder.append("; levels: ");
builder.append(maxLevel);
builder.append(" }");
return builder.toString();
}
}
public static void main(String[] args) {
SkipList list = new SkipList();
list.insert(1, 3);
list.insert(2, 3);
list.insert(3, 2);
list.insert(4, 4);
list.insert(5, 10);
list.insert(6, 4);
list.insert(8, 5);
list.insert(7, 4);
list.printAll_beautiful();
list.printAll();
SkipList list2 = new SkipList();
list2.insert2(1);
list2.insert2(2);
list2.insert2(6);
list2.insert2(7);
list2.insert2(8);
list2.insert2(3);
list2.insert2(4);
list2.insert2(5);
System.out.println();
list2.printAll_beautiful();
}
}打印结果
`null:15------- null:14------- null:13------- null:12------- null:11------- null:10------- 5:9------- 5:8------- 5:7------- 5:6------- 5:5------- 5:4-------8:4------- 4:3-------5:3-------6:3-------7:3-------8:3------- 1:2-------2:2-------4:2-------5:2-------6:2-------7:2-------8:2------- 1:1-------2:1-------3:1-------4:1-------5:1-------6:1-------7:1-------8:1------- 1:0-------2:0-------3:0-------4:0-------5:0-------6:0-------7:0-------8:0------- { data: 1; levels: 3 } { data: 2; levels: 3 } { data: 3; levels: 2 } { data: 4; levels: 4 } { data: 5; levels: 10 } { data: 6; levels: 4 } { data: 7; levels: 4 } { data: 8; levels: 5 }
null:15------- null:14------- null:13------- null:12------- null:11------- null:10------- null:9------- null:8------- null:7------- null:6------- null:5------- 5:4------- 3:3-------5:3------- 3:2-------4:2-------5:2-------7:2-------8:2------- 2:1-------3:1-------4:1-------5:1-------6:1-------7:1-------8:1------- 1:0-------2:0-------3:0-------4:0-------5:0-------6:0-------7:0-------8:0-------
`
代码来源github,并非本人编写:
https://github.com/wangzheng0822/algo/blob/master/java/17_skiplist/SkipList2.java
总结
什么是跳表?
跳表,全称:跳跃链表,在计算机科学中,跳跃列表是一种数据结构。它使得包含n个元素的有序序列的查找和插入操作的平均时间复杂度都是:logn
跳表的时间/空间复杂度
时间复杂度:O(logn),空间复杂度:O(n),空间复杂度会随着索引间隔距离的增大而减少,但是空间复杂度的趋势还是O(n)不变,由于索引层存储的信息相对于原始链表来说会少很多,所以即使是O(n)的空间复杂度,也是可以接受的。
跳表的应用
1.redis的有序集合。
2.google开源的key/value存储引擎。
3.HBase MemStore 内部存储结构
跳表的动态更新
由于跳表是由多层索引组成的,所以再频繁插入的时候会导致某一端相邻索引结点之前的数据过多,最坏情nixuefeileam况下,会导致所有的数据都集中在某一段相邻索引结点之间,这将会导致跳表退化成普通链表,时间复杂度也会退化到O(n),所以这个时候就需要动态的去更新跳表中的索引结点,目前通过随机函数实现。
为什么redis采用跳表实现有序集合?
1.跳表是链表+多级索引组成的数据结构,通过空间换时间的设计思路,实现了基于链表的“二分查找”,查找、删除、插入时间复杂度皆为:O(logn)。
2.跳表实现方式相对于B树、红黑树、AVL树等简单许多,这几种树的平衡维护相当麻烦,而跳表的动态索引更新相对来说就简单很多了。
3.跳表的区间查找要比红黑树等优秀。
朋友,你学废了吗?
以上是关于是什么让普通的链表也能达到二分查找的效率?没错,就是跳表的主要内容,如果未能解决你的问题,请参考以下文章