二分查找团灭力扣旋转排序数组系列

Posted 2021-04-23 程序员小熊

Leetcode 中有一系列 旋转排序数组 相关的问题，例如33. 搜索旋转排序数组、81. 搜索旋转排序数组 II、153. 寻找旋转排序数组中的最小值、154. 寻找旋转排序数组中的最小值 II 和面试题10.03 搜索旋转数组等，本文介绍通过二分查找团灭这一系列问题，供大家参考，希望能对大家有所帮助。

1

●

二分查找

●

【概念】

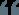
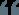
二分查找也称折半查找，是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。如下图示：

注：以下代码模板都是 C 语言的。

【代码模板（递归）】

int binarySearch(int* nums, int low, int high, int target) {
    if (low > right) {
        return -1;
    }

    /* 防止两个接近 2147483647 的整型数相加，导致溢出 */
    int mid = low + (high - low) / 2;
    /* target 小于中间元素，则在数组的前半区间查找 */  
    if (nums[mid] > target) { 
        return binarySearch(nums, low, mid - 1, target);
    /* target 大于中间元素，则在数组的后半区间查找 */    
    } else if (nums[mid] < target) { 
        return binarySearch(nums, mid + 1, high, target);
    /* target 等于中间元素，查找到目标值，查找结束 */
    } else if (nums[mid] == target) {
        return mid;
    } 
}

【代码模板（循环 左闭右闭 ）】

int binarySearch(int* nums, int numsSize, int target) {
    if (nums == NULL || numsSize <= 0) {
        return -1;
    }
 
    /* 在 [low...high] 的范围里查找target */
    int low = 0, high = numsSize - 1;
    /* 当 low == high 时，区间 [low...high] 依然是有效的 */
    while (low <= high) { 
        /* 防止整型溢出 */                       
        int mid = low + ((high - low) >> 1); 
        /* 找到 target，查找结束 */   
        if (nums[mid] == target) { 
            return mid;
        /* 中间元素大于 target，去 mid 左侧 [low, mid - 1] 查找 */         
        } else if (nums[mid] > target) { 
            high = mid - 1;
        /* 中间元素小于 target，去 mid 右侧 [mid + 1, high] 查找 */  
        } else if (nums[mid] < target) { 
            low = mid + 1; 
        }
    }
    return -1;
}

【代码模板（循环左闭右开）】

int binarySearch(int* nums, int numsSize, int target) {
    if (nums == NULL || numsSize <= 0) {
        return -1;
    }
 
    /* 在 [low...high) 的范围里查找 target */
    int low = 0, high = numsSize;
    /* 当 low == high 时，区间 [low...high) 依然是无效的 */
    while (low < high) { 
        /* 防止整型溢出 */                       
        int mid = low + ((high - low) >> 1); 
        /* 找到 target，查找结束 */   
        if (nums[mid] == target) { 
            return mid;
        /* 中间元素大于 target，去 mid 左侧 [low, mid) 查找 */         
        } else if (nums[mid] > target) { 
            high = mid;
        /* 中间元素小于 target，去 mid 右侧 [mid + 1, high) 查找 */  
        } else if (nums[mid] < target) { 
            low = mid + 1; 
        }
    }
    return -1;
}

写循环版本的二分查找代码的核心在于：清晰定义左右边界 low 和 high 具体表达的含义，在循环查找中就需要不断维护这个含义。循环中不断维护 low 和 high 的含义，也就是说在循环中保证了一个循环不变量。

【循环不变量】

2

●

33. 搜索旋转排序数组

●

【题目】

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的索引，否则返回 -1 。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

提示：

1 <= nums.length <= 5000

-10^4 <= nums[i] <= 10^4

nums 中的每个值都 独一无二

nums 肯定会在某个点上旋转

-10^4 <= target <= 10^4

【解题思路】

升序数组在某个下标 k（0 <= k < nums.length）上旋转之后，数组可以分成两部分，其中一部分一定是有序的，另一部分可能是有序的，也可能是无序的。因此可以在有序的部分可以采用二分查找。无序部分再一分为二，采用同样的策略查找。由于题目中已明确了数组中的值互不相同，因此不需要考虑有相同值的情况。

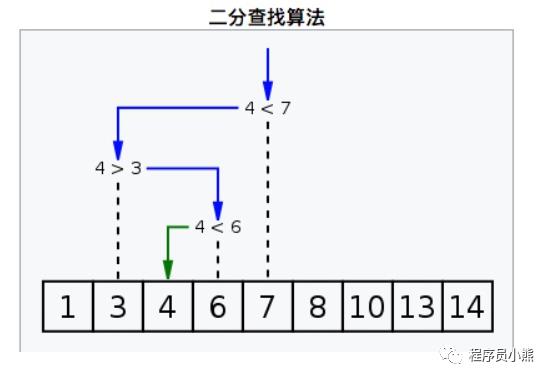
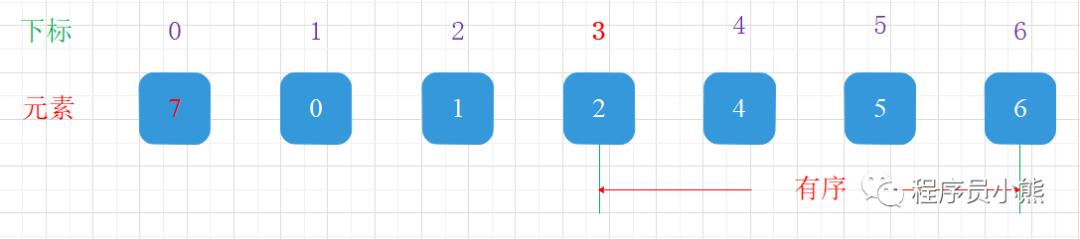
以数组 nums = [0,1,2,4,5,6,7] 为栗子，其中下标 3 为点，如下图示：




在下标 3 旋转之后，数组为 [4,5,6,7,0,1,2]，其中数组的前半部分 [0, 3] 有序




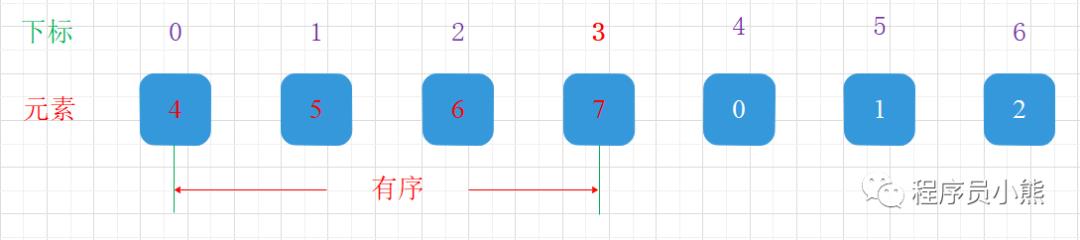
在下标 5 旋转之后，数组为 [7,0,1,2,4,5,6]，其中数组的后半部分 [3, 6] 有序




【Show me the Code】

// c 语言
int search(int* nums, int numsSize, int target){
    int l = 0, r = numsSize - 1;
    while (l <= r) {
        int m = l + ((r - l) >> 1);
        /* 查找到 target，直接返回下标 */
        if (nums[m] == target) {
            return m;
        }

        /* 数组前半部分有序 */
        if (nums[l] <= nums[m]) {
            /* target 在排序数组旋转之后的前半部分（有序）中 */
            if (nums[l] <= target && target < nums[m]) {
                r = m - 1;
            /* target 在排序数组旋转之后的后半部分中 */
            } else {
                l = m + 1;
            }
        /* 数组后半部分有序 */    
        } else {
            /* target 在排序数组旋转之后的后半部分（有序）中 */
            if (nums[m] < target && target <= nums[r]) {
                l = m + 1;
            /* target 在排序数组旋转之后的前半部分中 */    
            } else {
                r = m -1;
            }
        }
    }
    return -1;
}

3

●

81. 搜索旋转排序数组   II

●

【题目】

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。

编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true，否则返回 false。

示例 1:

输入: nums = [2,5,6,0,0,1,2], target = 0
输出: true

【解题思路】

本题跟 33 题类似，唯一的不同就是数组 nums 可能包含重复元素。例如像nums = [2,2,2,3,1] 这种（nums[l] == nums[m]），此时只需要将左边界 l 右移并不断判断其对于的数组元素的值是否等于 nums[m]，去掉重复的干扰项，就跟 33 题完全一样，采用 33 题的解法即可。

【Show me the Code】

// c++
bool search(vector<int>& nums, int target) {
    int l = 0, r = nums.size() - 1;
    while (l <= r) {
        int m = l + ((r - l) >> 1);
        /* 查找到 target，直接返回 */
        if (nums[m] == target) {
            return true;
        } 

        /* 存在重复元素，左边界右移去掉重复元素 */
        if (nums[l] == nums[m]) {
            l++;
            continue;
        }
        
        /* 数组前半部分有序 */
        if (nums[l] <= nums[m]) {
            /* target 在排序数组旋转之后的前半部分（有序）中 */
            if (nums[l] <= target && target < nums[m]) {
                r = m - 1;
            /* target 在排序数组旋转之后的后半部分中 */    
            } else {
                l = m + 1;
            }
        /* 数组后半部分有序 */    
        } else {
            /* target 在排序数组旋转之后的后半部分（有序）中 */
            if (nums[m] < target && target <= nums[r]) {
                l = m + 1;
            /* target 在排序数组旋转之后的前半部分中 */     
            } else {
                r = m - 1;
            }
        }
    }
    return false;
}

4

●

面试题 10.03. 搜索旋转数组

●

【题目】

搜索旋转数组。给定一个排序后的数组，包含n个整数，但这个数组已被旋转过很多次了，次数不详。请编写代码找出数组中的某个元素，假设数组元素原先是按升序排列的。若有多个相同元素，返回索引值最小的一个。

示例1:

 输入: arr = [15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14], target = 5

 输出: 8（元素5在该数组中的索引）

【解题思路】

由于无论升序数组旋转过多少遍，旋转后的数组有一边（左边或右边）必定还是按照升序排列的。因此可以通过比较 arr[l] 与 arr[m]，判断旋转后的数组升序部分是在哪一边，再确定应该搜索左边还是右边。需要注意这种用例 arr= [3,3,0,1,3], target = 1。

【Show me the Code】

// c 语言
int search(int* arr, int arrSize, int target){
    /* 搜索区间 [0, arrSize - 1] */
    int left = 0, right = arrSize - 1; 
    /* 维持在区间 [left, right] 中搜索 */
    while (left <= right) { 
        /* 防止整型溢出 */             
        int mid = left + (right - left) / 2; 
        /* arr在区间 [left, mid] 升序 */    
        if (arr[left] < arr[mid]) { 
            /* target 在区间 [left, mid] 中，缩小右边界 */                
            if (arr[left] <= target && target <= arr[mid]) { 
                right = mid;
            /* target 在区间（mid, right] 中 */    
            } else { 
                left = mid + 1;
            }
        /* 在区间 [left, mid] 不升序 */
        } else if (arr[left] > arr[mid]) {
            /* target 在区间（mid, right] 中 */
            if ((arr[mid] < target) && ((target <= arr[right]) && (arr[left] > arr[right]) || target < arr[right])) { 
                left = mid + 1;
            /* target 在区间 [left, mid] 中 */    
            } else { 
                right = mid;
            }
        /* 存在重复的元素 */    
        } else if (arr[left] == arr[mid]) { 
            if (arr[left] != target) {
                left++;
            } else {
                return left; 
            }
        }
    }
    return -1;
}

往期精彩回顾

动态规划经典题之最长上升子序列最终版

Dine，公众号：程序员小熊

分享、在看与点赞都在这儿

点下给小编加点料