基于轮廓系数的高维数据K-Means聚类算法处理
Posted 智能科技之芯
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于轮廓系数的高维数据K-Means聚类算法处理相关的知识,希望对你有一定的参考价值。
基于轮廓系数的高维数据K-Means聚类算法处理


机器学习中有相当一部分的算法属于无监督学习算法,无监督学习往往是没有足够的先验知识,在训练的时候只需要根据特征矩阵X,往往不需要标签。聚类算法就是无监督学习算法的代表之一。
但是,现实中的很多实验,采集的数据经常是具有很多特征的高维数据,我们如何对高维数据进行聚类研究,首先,我们就可以通过PCA对高维数据进行降维,使其降低至2维数据,之后通过聚类K-Means算法对其进行聚类处理,这样我们就可以将高维数据进行二维可视化。具体实例如下。



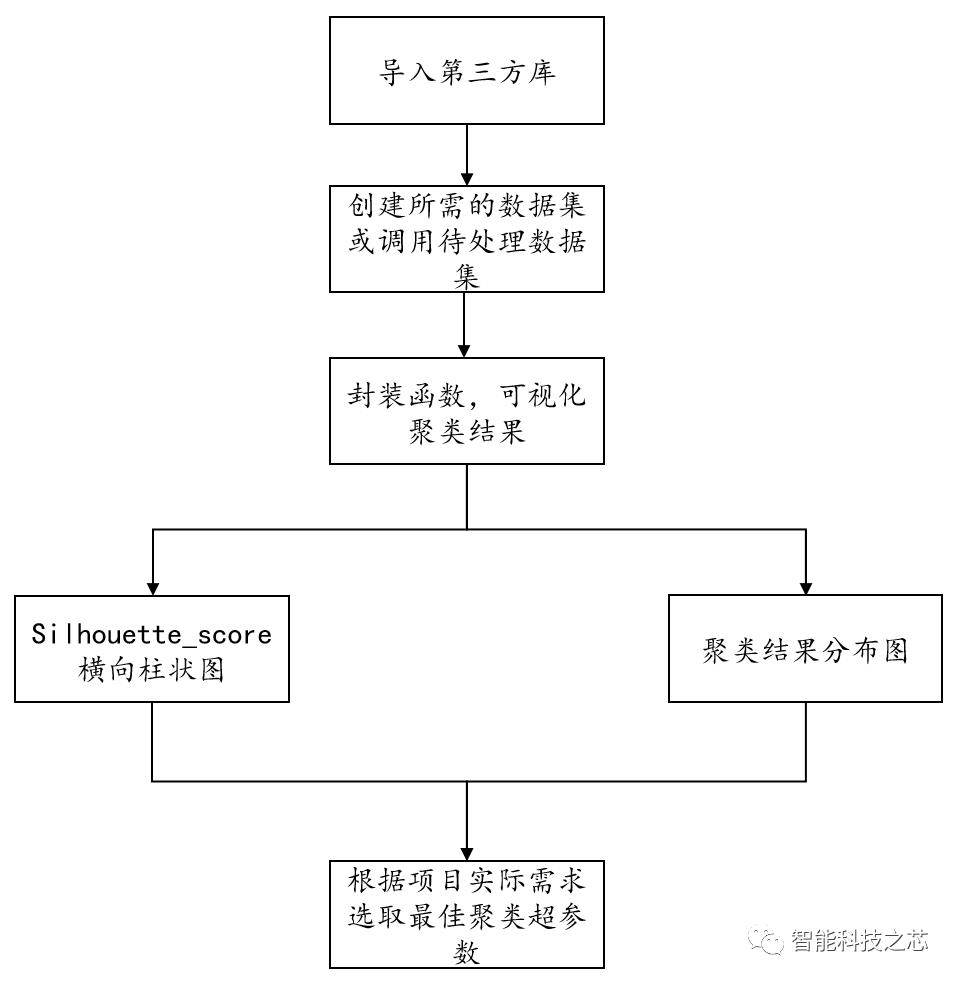
一、导入我们所需的sklearn库
from sklearn.cluster import KMeans
from sklearn.metrics import
silhouette_samples,silhouette_score
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np


二、创建自己所需要的数据集,这里的数据集样本为500,特征数目为7,聚类数目为4,随机数种子采用100;
from sklearn.datasets import make_blobs
from sklearn.decomposition import PCA
a,y =
make_blobs(n_samples=500,n_features=7,centers=4,random_state=100)
#对处理过的数据进行PCA降维处理;
x = PCA(n_components=2).fit_transform(a)


三、封装我们所需的聚类函数,并且设置我们的可视化图形
for s in list(np.arange(2,7)):
#分成的簇的数目;
n_clusters = s
#一个画布,两个图;
fig,(ax1,ax2) = plt.subplots(1,2)
fig.set_size_inches(18,7)
#第一个图是横向条形图;
#横坐标是轮廓系数的取值;纵坐标是样本取值;
ax1.set_xlim([-0.1,1])
#纵坐标是使得每个簇可以排列在一起,不同的簇之间有一定的间隙;
ax1.set_ylim([0,x.shape[0]+
(n_clusters+1)*10])
clusterer =
KMeans(n_clusters=n_clusters,random_state=10).fit(x)
cluster_labels = clusterer.labels_
#返回一个数据集中,所有样本的轮廓系数的均值
silhouette_avg =
silhouette_score(x,cluster_labels)
print("For n_clusters =",n_clusters,
"The average silhouette_score
is :",silhouette_avg)
#返回的是数据集中,每个样本自己的轮廓系数;
sample_silhouette_values
=silhouette_samples(x,cluster_labels)
四、聚类结果可视化-横向柱状图
y_lower = 10
for i in range(n_clusters):
#从每个样本的轮廓系数结果中抽取第i个簇的轮廓系数;并进行排序;
ith_cluster_silhouette_values =
sample_silhouette_values[cluster_labels ==i]
ith_cluster_silhouette_values.sort()
#查看这一个簇中有多少个样本;
size_cluster_i =
ith_cluster_silhouette_values.shape[0]
#确定纵坐标中簇的连续间隔;
y_upper = y_lower + size_cluster_i
#使用小数来调用颜色的函数;
color =
cm.nipy_spectral(float(i)/n_clusters) ax1.fill_betweenx(np.arange(y_lower,y_upper),ith_cluster_silhouette_values,facecolor=color,alpha=0.7)
#显示文本text(横坐标,纵坐标,内容)
ax1.text(-0.05,y_lower+0.5*size_cluster_i,str(i))
#循环往纵坐标上面走;
y_lower = y_upper + 10
#把整个数据集上的轮廓系数的均值以虚线的形式放入图中;
ax1.axvline(x=silhouette_avg,color='red',
linestyle='--')
ax1.set_yticks([])


五、聚类分布图可视化
colors =
cm.nipy_spectral(cluster_labels.astype(float)/n_clusters)
ax2.scatter(x[:,0],x[:,1],marker='o',s=8,c=colors)
#画出聚类的中间点;
centers = clusterer.cluster_centers_
ax2.scatter(centers[:,0],centers[:,1],marker='x',c='red',alpha=1,s=200)



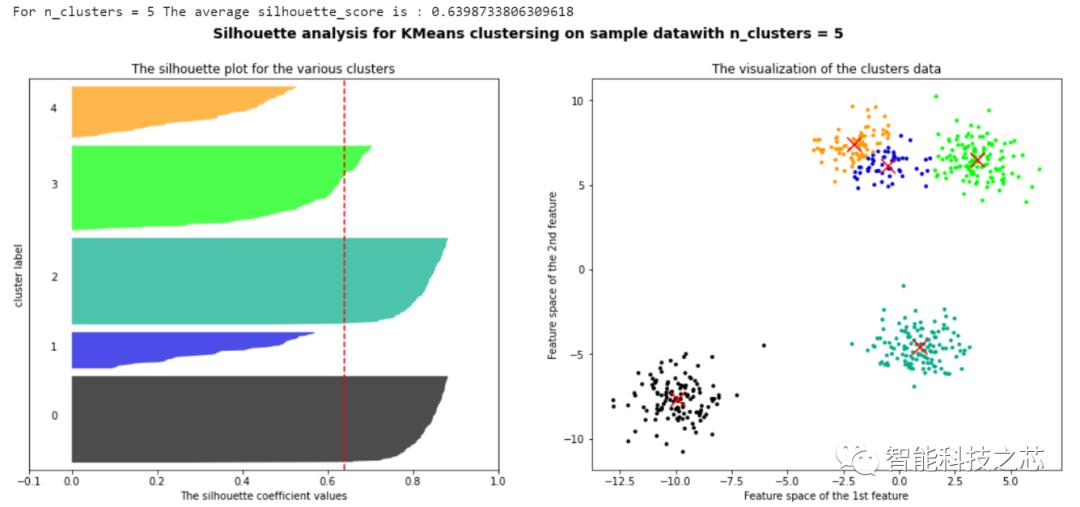
通过聚类结果可视化可以看出,当这组数据聚类数为3时,其返回的一个数据集中,所有样本的轮廓系数的均值最高,但是,聚类分析是没有办法给出那种聚类结果最好的,我们只能根据实际的项目分析,选取最合适的聚类数目进行研究。这种通过PCA对高维数据进行降维的方法,可以有效地帮助我们处理高维特征的数据集,并且通过轮廓系数来确定所需要的超参数。


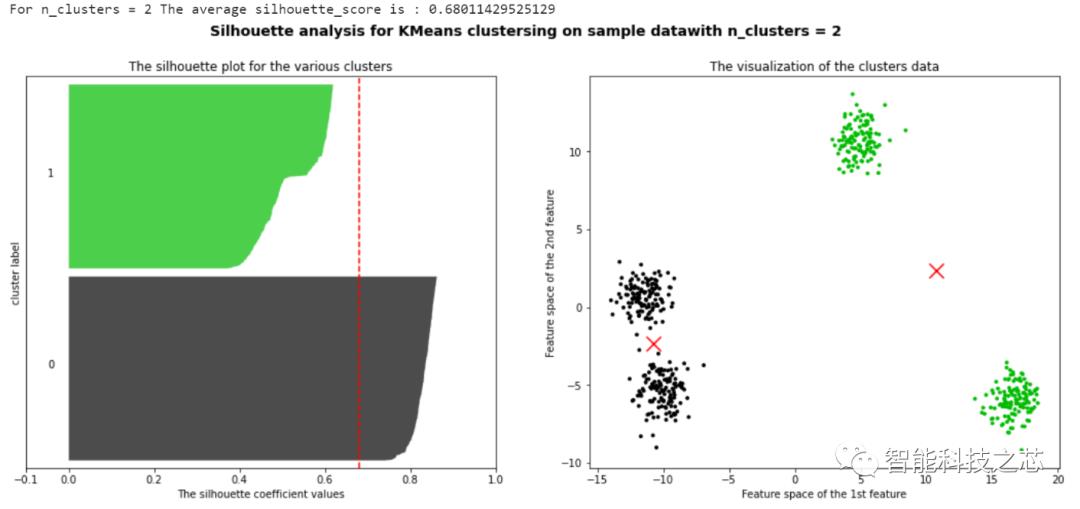
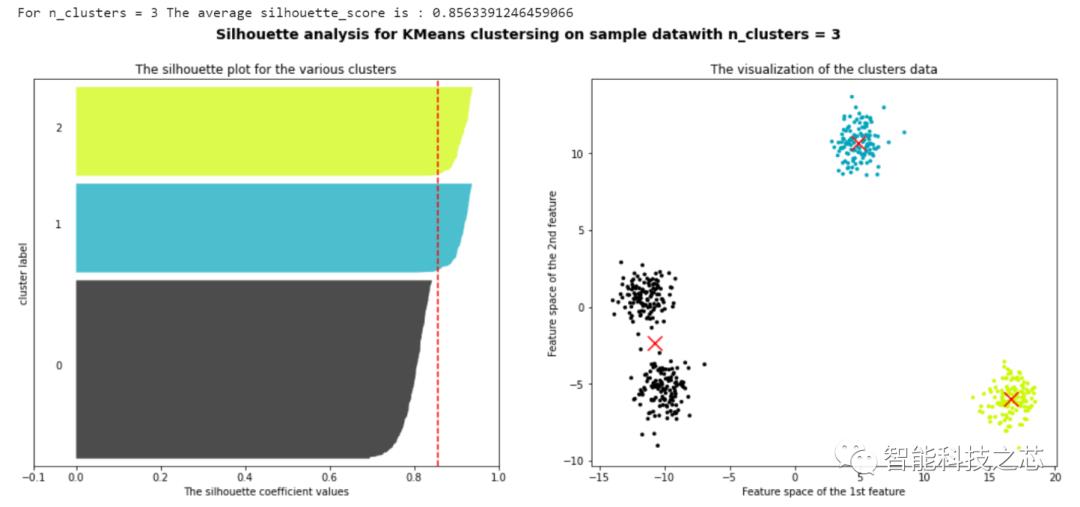
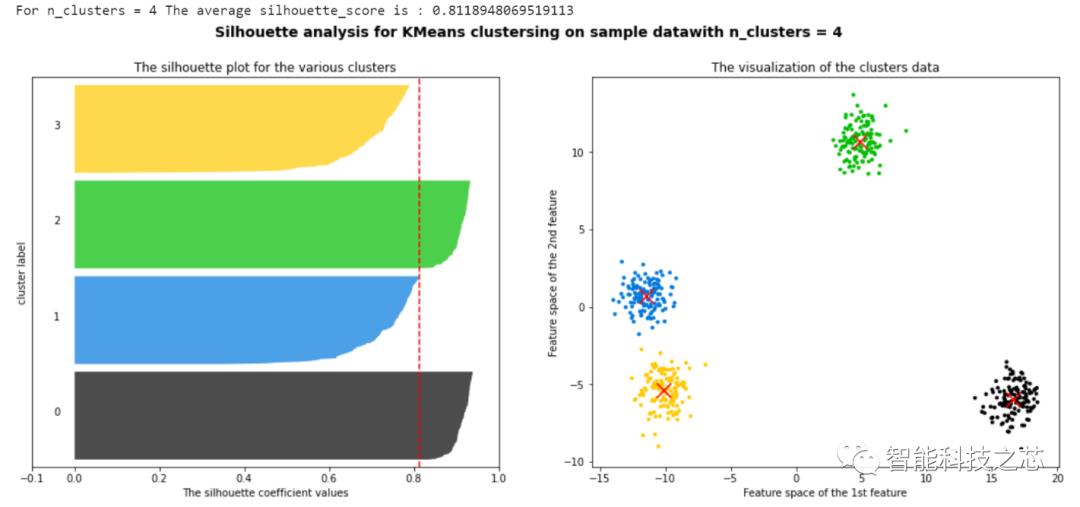
以上是关于基于轮廓系数的高维数据K-Means聚类算法处理的主要内容,如果未能解决你的问题,请参考以下文章