朴素贝叶斯算法以及ROC和PR曲线

Posted 2021-04-24 R语言数据分析与建模

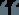
朴素贝叶斯（Naviebayes)的原理很简单：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为该代分项属于哪个类别？

第一阶段：准备工作阶段。这个阶段的任务为朴素贝叶斯分类做必要的准备。主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对部分待分选项进行分类，形成训练样本集合。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程产生重要影响。

第二阶段：分类器训练阶段。这个阶段的任务是生成分类器，主要工作是计算每个类别在训练样本中出现的概率以及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。分类的质量很大程度上由特征属性，特征属性划分以及训练样本质量决定。这一阶段是机械性阶段，可以有程序自动完成

第三阶段：应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分项，输出是待分项和类别的映射关系，由程序进行完成。

set.seed(1234)

ind<-sample(2,nrow(Data),replace=TRUE,prob = c(0.7,0.3))

Data[,"流失"]=as.factor(Data[,"流失"])

traindata<-Data[ind==1,]

library(e1071)

naiveBayes.model<-naiveBayes(流失~.,data=traindata)

train_predict=predict(naiveBayes.model,newdata = traindata)

test_predict=predict(naiveBayes.model,newdata = testdata)

train_predictdata=cbind(traindata,predictedclass=train_predict)

train_confusion=table(actual=traindata$流失,predictedclass=train_predict)

train_confusion

test_predictdata=cbind(testdata,predictedclass=test_predict)

test_confusion=table(actual=testdata$流失,predictedclass=test_predict)

test_confusion

train_confusion

      predictedclass

actual   0   1

6     0 314 184

     1  40 160

 test_confusion

      predictedclass

actual   0   1

     0 134  94

     1  24  50

我们也讲了几个算法了，接下来看看模型的预测模型的效果是如何来衡量的呢？

一般的指标有这几种：1.绝对误差和相对误差2.平均绝对误差3.均方差误差与均方根误差4.识别准确度5.识别精准率6.反馈率7.混淆矩阵8.ROC曲线和PR曲线

受试者工作特性（receiver Operating Characteristic,ROC）是一种非常有效的模型评价方法，可作选定临界值给出的定量提示。将灵敏度（sensitivity）设在纵轴，1-特异性（1-specificity)设在横轴，就可以得到ROC曲线。该曲线下的积分面积（Area)大小与每种方法的优劣密切相关，反映分类器在正确分类的统计概率，其值越接近1，说明该算法效果越好。

PR曲线指的是Precision Recall曲线。如果是分类器的话，可以调分类阀值，可以得到不同的PR值，从而可以得到一条曲线（纵坐标代表识别精准率，横坐标代表反馈率）。通常随着阀值从大到小的变化，识别精准率减小，反馈率增加。比较两个分类器好坏时，PR曲线越往坐标（1，1）的位置靠近越好。

library(ROCR)

library(gplots)

train_predict=predict(lda.model,newdata = traindata)

test_predict=predict(lda.model,newdata = testdata)

par(mfrow=c(1,2))

predi<-prediction(train_predict$posterior[,2],traindata$流失)

perfor<-performance(predi,"tpr","fpr")

plot(perfor,col="red",type="l",main="ROC曲线")

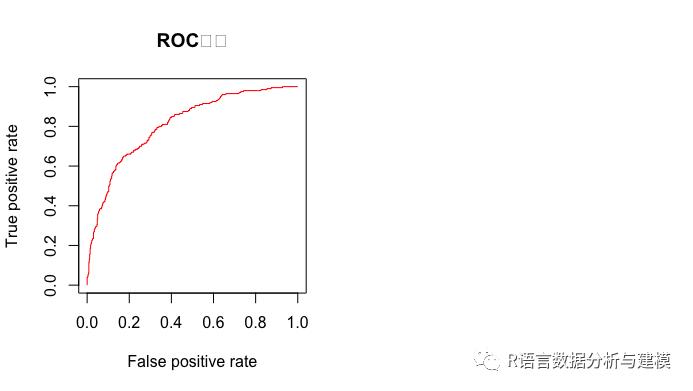
predi2<-prediction(test_predict$posterior[,2],testdata$流失)

perfor2<-performance(predi2,"tpr","fpr")

par(new=T)

plot(perfor2,col="blue",type="l",pch=2)

abline(0,1)

legend("bottomright",legend =c("训练集","测试集"),bty="n",lty=c(1,2),col=c("red","blue"))

prefor<-performance(predi,"prec","rec")

plot(perfor,col="red",type="l",main="PR曲线",xlim=c(0,1),ylim=c(0,1),lty=1)

perfor2<-performance(predi2,"prec","rec")

par(new=T)

plot(perfor2,col="blue",type="l",pch=2,xlim=c(0,1),ylim=c(0,1),lty=2)

abline(1,-1)

legend("bottomleft",legend=c("训练集","测试集"),bty="n",lty = c(1,2),col=c("red","blue"))

基本概念再来复习以下

1、roc曲线：接收者操作特征(receiveroperating characteristic),roc曲线上每个点反映着对同一信号刺激的感受性。

横轴：负正类率(false postive rate FPR)特异度，划分实例中所有负例占所有负例的比例；(1-Specificity)

纵轴：真正类率(true postive rate TPR)灵敏度，Sensitivity(正类覆盖率)

2针对一个二分类问题，将实例分成正类(postive)或者负类(negative)。但是实际中分类时，会出现四种情况.

(1)若一个实例是正类并且被预测为正类，即为真正类(True Postive TP)

(2)若一个实例是正类，但是被预测成为负类，即为假负类(False Negative FN)

(3)若一个实例是负类，但是被预测成为正类，即为假正类(False Postive FP)

(4)若一个实例是负类，但是被预测成为负类，即为真负类(True Negative TN)

TP:正确的肯定数目

FN:漏报，没有找到正确匹配的数目

FP:误报，没有的匹配不正确

TN:正确拒绝的非匹配数目

列联表如下，1代表正类，0代表负类：

由上表可得出横，纵轴的计算公式：

(1)真正类率(True Postive Rate)TPR: TP/(TP+FN),代表分类器预测的正类中实际正实例占所有正实例的比例。Sensitivity

(2)负正类率(False Postive Rate)FPR: FP/(FP+TN)，代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity

(3)真负类率(True Negative Rate)TNR: TN/(FP+TN),代表分类器预测的负类中实际负实例占所有负实例的比例，TNR=1-FPR。