清华AIOps算法：KPI聚类

Posted 2021-04-24 智能运维前沿

作者｜李之涵 张明

编辑｜Vicky

简介

在大型互联网企业中，对海量KPI（关键性能指标）进行监控和异常检测是确保服务质量和可靠性的重要手段。本文介绍清华大学NetMan实验室发表于IWQoS 2018的研究成果：ROCKA——一种快速、鲁棒的KPI聚类算法，用于辅助大规模KPI异常检测任务，实现高效、准确的大规模异常检测。

问题场景

基于互联网的服务型企业（如线上购物、社交网络、搜索引擎等）通过监控各种系统及应用的数以万计的KPI（如CPU利用率、每秒请求量等）来确保服务可靠性。KPI上的异常通常反映了其相关应用上可能出现故障，如服务器故障、网络负载过高、外部攻击等。因而，异常检测技术被广泛用于及时检测异常事件以达到快速止损的目的。

然而，大多数前沿的异常检测算法（如Opprentice，EDAGS，DONUT）都需要为每条KPI单独建立异常检测模型，在面对海量KPI时，会产生极大的模型选择、参数调优、模型训练及异常标注开销。幸运的是，由于许多KPI之间存在隐含的关联性，它们是较为相似的。如果我们能够找到这些相似的KPI（例如在一个负载均衡的服务器集群中每个服务器上的每秒请求量KPI是相似的），将它们划分为若干聚类簇，则可以在每个聚类簇中应用相同的异常检测模型，从而大大降低各项开销。

KPI本质上是一种时序数据，对KPI的聚类主要面临两种挑战：其一，KPI曲线上的噪声、异常、相位偏差和振幅（量纲）差异通常会改变KPI曲线的形状，从而影响对KPI的相似性判别，难以用传统方法实现快速准确的聚类。其二，一条KPI曲线通常包含上万个数据点，时间跨度从几天到数周，从而完整的刻画其曲线模式（例如周期性、季节性等）。因此，KPI曲线通常具有较高的维度，进一步增加了对聚类的挑战。

面对这些问题，本文所介绍的ROCKA算法着眼于KPI聚类这一问题，提出一种高效、鲁棒的基于曲线形状的KPI聚类算法，在实际KPI数据集上取得了很好的效果。同时，作者利用ROCKA辅助KPI异常检测任务，以较少的准确性损失为代价极大的降低了异常检测算法的模型训练时间。

算法框架

KPI是一种特殊的时序数据，与普通时序数据相比，存在更多的形状变化（shape variations）。常见的形状变化主要包括以下几种，如图1所示：

• 噪声和异常：曲线上与正常值不符的波动

• 振幅差异：KPI曲线可能具有不同量级的振幅，例如同一服务的两个相关但不同模块的QPS曲线。

• 相位偏差：两条KPI曲线之间的整体相位偏移。例如，同一系统调用链上的一组KPI可能具有相似的形状，但存在一定的时延，从而产生相位偏差。

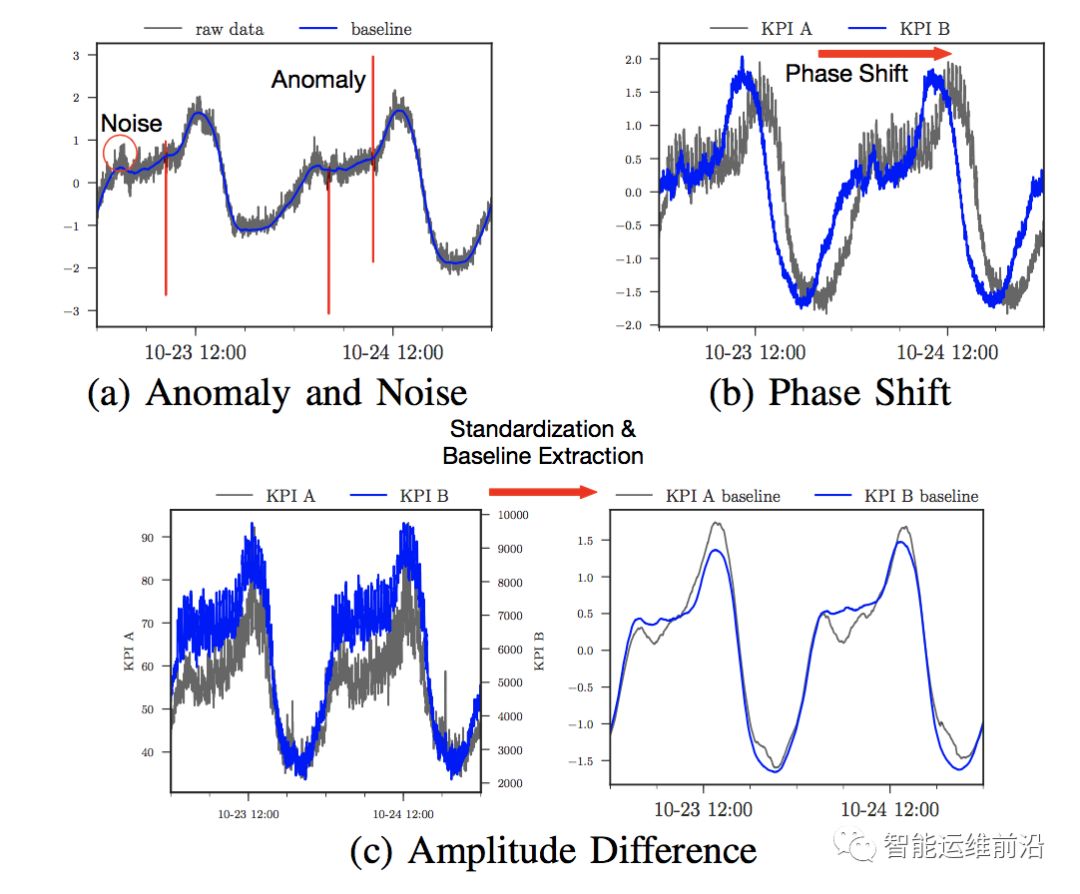
图1  KPI曲线上的常见形状变化

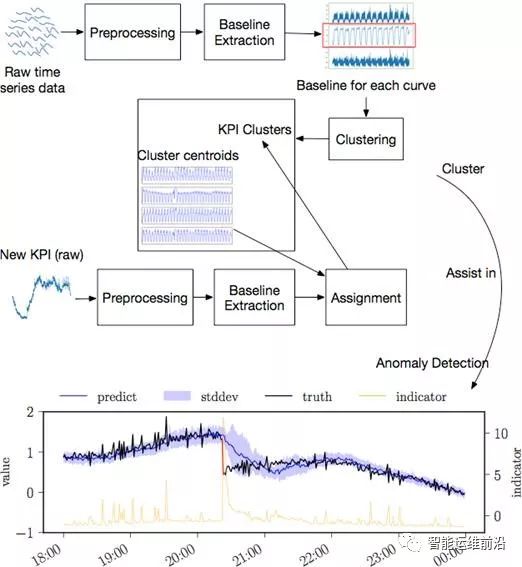
这些变化会干扰KPI曲线相似性的计算。此外，处理高维的KPI曲线也要求聚类算法需要具有较低的计算复杂度。为解决这些问题，作者提出了针对KPI曲线的聚类算法ROCKA，算法框架如图2所示。整套算法包含如下几个关键步骤：

• 预处理：对原始KPI数据进行标准化，消除振幅差异。

• 基线提取：去除曲线上的噪声和可能的异常点，提取基线来表示曲线的形状。

• 相似性度量：采用基于形状的SBD距离作为相似性度量，消除曲线间的相位偏差影响。

• 聚类与分派：对样本集中的KPI进行高效、鲁棒的聚类，为每个类别计算聚类中心表征该类别曲线形状。对于大量未分类曲线，利用聚类中心为其快速分派类别。

   

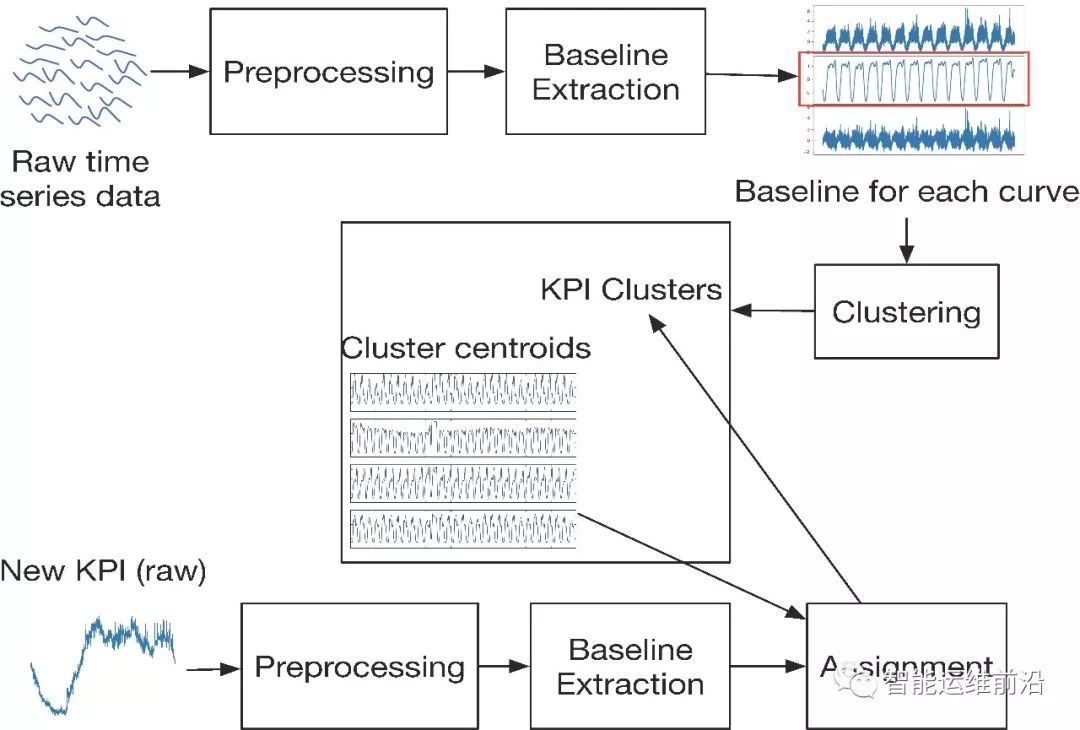
图2  ROCKA算法框架

算法细节

下面分别对这些关键步骤进行简要叙述。

1. 预处理

对于KPI中存在的少量缺失值，采用线性插值进行填充。之后对每条原始KPI数据进行标准化（standardization）得到均值为0方差为1的曲线，消除振幅差异的影响，从而能够比较不同系统及应用的KPI之间的相似性。

2. 基线提取

作者通过提取基线来表征KPI曲线的潜在模式，降低噪声和异常对相似性判别的影响。具体的，首先要平滑一些极端异常值。通常，曲线上的异常点比例不超过5%。因此，通过去除偏离均值最远的5%的数据点，并使用其相邻的正常观测值对这些点做线性填充，即可去除多数极端异常值。特别的，对于异常较少的曲线，即使某些正常值被去除，它们仍会被其他正常值插值填充，从而不会影响到KPI曲线的潜在模式。

此外，一条实际KPI曲线可被视为一条平滑的基线（表征了曲线的正常模式）和许多随机噪声组成。一个简单有效的去除噪声的方法是在KPI曲线上使用一个小的滑动窗口做滑动平均，将曲线分为基线与余项两部分。对于KPI T，应用大小为W的滑动窗口，步长为1，其基线B和余项R可由下式计算，效果如图3所示。

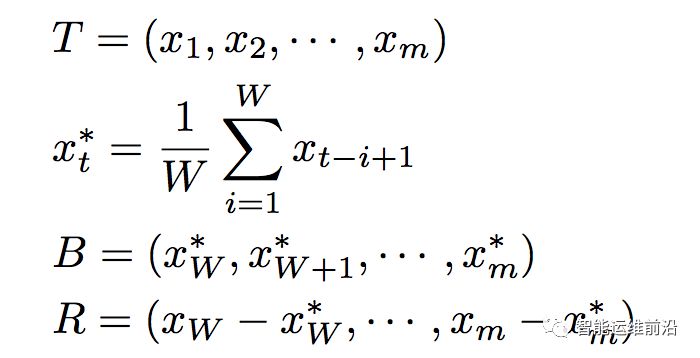
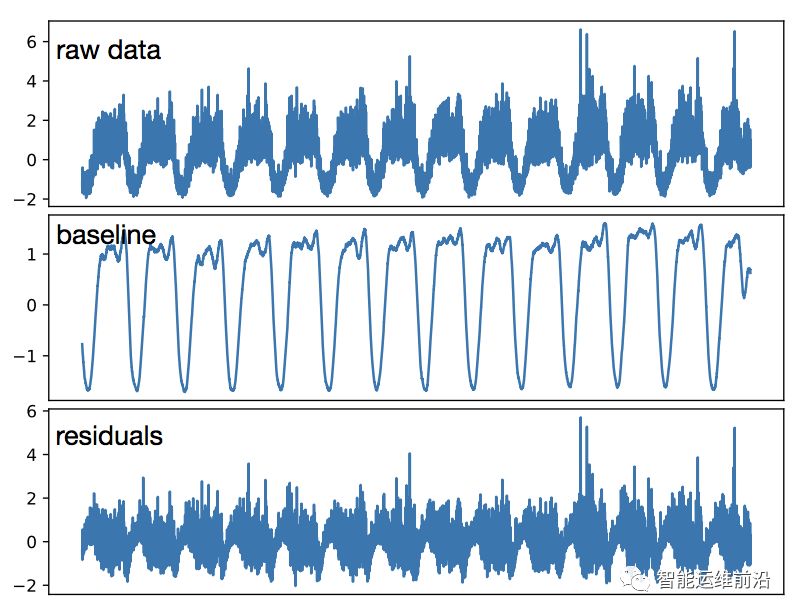
图3  真实KPI的基线提取

由此步骤得到的基线去除了KPI曲线上的大量噪声和异常值，并保留了KPI的模式特征。标准化的基线被用于后续的聚类算法中。

3. 相似性度量

为了判别KPI曲线间的形状相似性，作者对基线使用一种基于互相关（cross-correlation）距离度量SBD来比较它们的相似性。互相关计算两条时序数据之间的滑动内积，常用于信号处理领域，对于相位偏差具有天然的鲁棒性。对于两条时序曲线x、y及相位偏差s，标准化互相关NCC及距离度量SBD可计算如下：

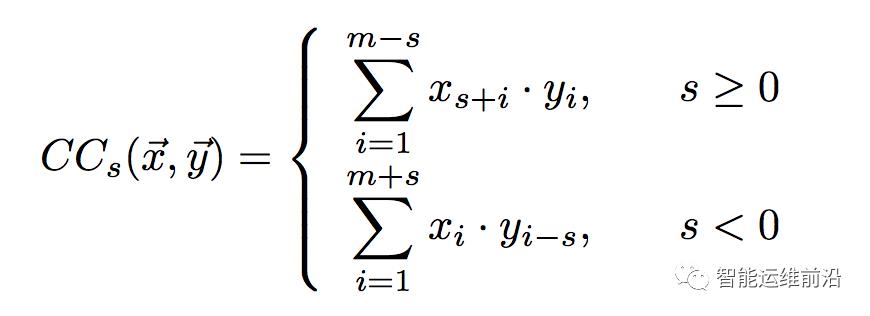
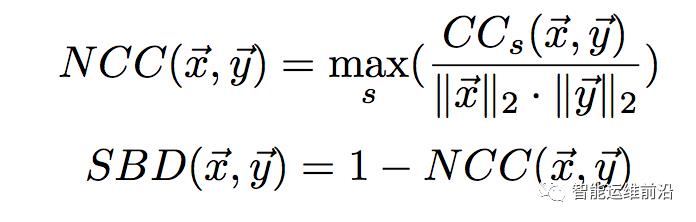
直观上讲，在最优偏移s时，x和y中的相似模式被对齐（proper aligned）从而使内积最大（例如，在最优偏移时x中的峰与曲线y上相似的峰对齐，从而使其乘积最大）。将这种基于互相关的相似性度量应用于KPI的基线上，从而克服曲线间的相位偏差，刻画其形状相似性。NCC的值域为[-1, 1]，因而距离度量SBD的值域为[0,2]，为0时表示两曲线具有完全相同的形状。SBD值越小表示两曲线的形状相似性越高。特别的，利用卷积理论和快速傅立叶变换，可将计算两条长度为m的KPI的时间复杂度降至O(mlogm)，从而快速计算曲线间的相似性。

4. 聚类与分派

利用相似性度量SBD，作者采用基于密度的聚类算法DBSCAN对随机采样的部分KPI进行聚类。DBSCAN的核心思想是根据所用的相似性度量在样本的稠密区域中找到若干核心样本（cores），之后通过样本相似性的传递性来扩展各核心样本所在的区域（即若a与b相似，b与c相似，则a、b、c均属于同一聚类簇），形成聚类簇。这一思路正与SBD距离契合，能够按照KPI曲线的潜在模式相似性进行聚类，并可以形成任意形状和大小的聚类簇。

为确定DBSCAN算法中的关键参数密度半径，作者使用一种启发式的算法来确定密度半径的值。具体的，对于待聚类的KPI样本集，计算每个样本的k近邻距离（样本到与其第k近的样本间的距离），按降序排列形成k-距离曲线。曲线上的平坦部分为候选半径值，而陡峭部分则对应密度的剧烈变化，不适合作为密度半径。此外，对于相似性距离SBD而已，越小的SBD值表明曲线越相似，而较大的SBD值则表明曲线间不相似，如图4所示。因此，结合互相关的理论，作者采用经验值0.05作为上界，将不超过此值的最大候选半径作为最终的密度半径值，在其使用的各数据集上均取得了很好的效果。实际使用中，可以通过调节上界来获得不同粒度的聚类簇。即，较大的上界能够获得少量的粗粒度聚类簇，而较小的上界会得到较多的细粒度聚类簇，但也会导致更多样本被划分为离群点（outliers，表明该样本与各聚类簇均不相似）。

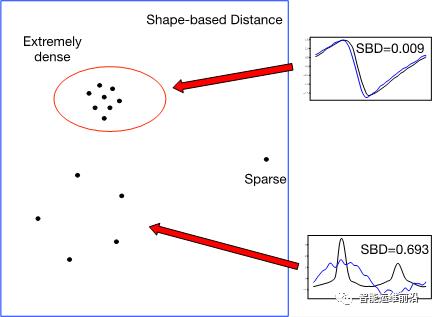
图4  SBD距离下的密度区域示意

对于样本集中得到的聚类簇，由下式计算各聚类簇的聚类中心，表征该类别的形状特征：

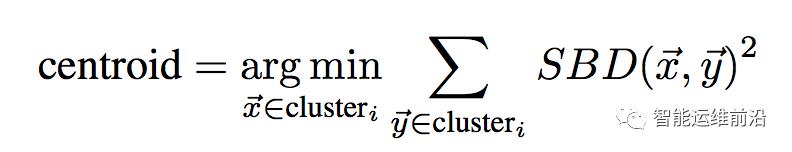
对于大量的未分类曲线，只需计算其与各聚类中心的相似性距离，将其分派到距离最近的类别。特别的，互相关理论中通常认为NCC小于0.8（对应SBD距离大于0.2）意味着两曲线没有强相关性，因而，若一条KPI与各聚类中心的SBD距离均大于0.2，则该KPI被划分为离群点，表明其与任何聚类簇在形状上均不相似。由此，通过快速的分派策略，能够快速对海量KPI根据形状进行分类。一组标准化后的KPI组成的聚类簇如图5所示，其中红色曲线为聚类中心，表征了该类别的形状特征。

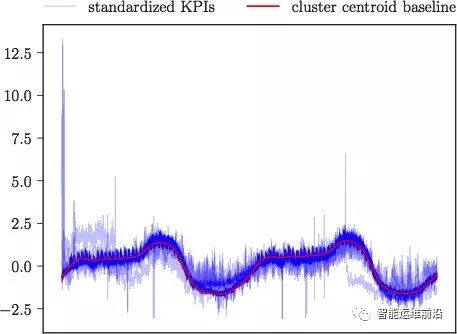
图5  KPI聚类簇及聚类中心

实验验证

作者在3个公开时序数据集及2个真实KPI数据集上对算法的性能和效率进行了测试，并与前沿的大规模时序曲线聚类算法YADING相比较。

在三个公开数据集上，算法ROCKA均取得了超越YADING的效果（如图6所示），且达到与YADING相仿的计算效率。

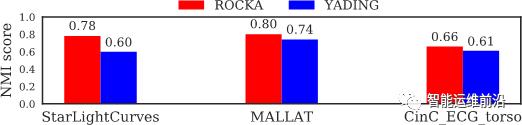
图6  公开时序数据集效果

对于真实KPI数据，作者采用了两个数据集进行评测。数据集1是来自不同集群机器的TPS／QPS数据，数据集2是来源于大量机器的机器级别指标（例如响应时间、CPU利用率等）。如表1所示，ROCKA在两数据集上均取得了很好的准确率（F-score）及计算效率，且仅有少数曲线被划分为离群点。而YADING仅采用简单的L1距离作为度量，且未做对异常点和相位偏差的处理。虽然也达到了较高准确率，但有近半的曲线被其划分为离群点。即，YADING仅将十分相似的曲线划分为若干小聚类簇，而对异常、噪声、相位偏差等形状变化鲁棒性较差，从而将大量曲线误分为离群点。这对于大规模的KPI异常检测并不能起到有效帮助。

表1  真实KPI数据集上的性能对比

此外，作者还比较了算法中三项主要技术（基线提取、SBD度量、基于密度的聚类）对算法效率、性能和鲁棒性的影响，三项技术的结合有效提升了算法对于KPI曲线各种形状变化的鲁棒性，提高了算法的性能和效率（具体结果见原文）。

ROCKA辅助异常检测

最后展示的是ROCKA实际用于辅助异常检测任务的效果。作者将ROCKA与刚发表在WWW 2018上的前沿异常检测算法DONUT相结合，说明如何使用ROCKA辅助大规模异常检测。

DONUT训练一个深度生成模型来重构KPI数据，在KPI上利用滑动窗口得到小段时间序列x，并识别x所应遵循的正常模式。根据x与正常模式的差别计算出异常分数，表征其异常程度。在实际使用中，通过选择一个阈值，将异常分数超过阈值的点视为异常进行告警。

在面临大量KPI时，DONUT为每条KPI单独训练模型进行异常检测，将面临较大的模型训练等开销。然而，ROCKA的设计根据KPI曲线的潜在模式对其进行聚类，正契合类似DONUT这种识别曲线正常模式进行异常检测的方法。作者设计三组实验进行对比，证明ROCKA辅助异常检测的有效性和可行性。

• E1: 仅使用原始DONUT为每条KPI训练模型进行异常检测，按原作者的方法为每条KPI调优寻找能取得最佳F-score的阈值。

• E2: ROCKA+DONUT。利用ROCKA对KPI曲线进行聚类并求出聚类中心。仅在聚类中心曲线上训练DONUT模型，并选出最佳阈值。将聚类中心的模型及阈值应用于同聚类簇的其他KPI曲线上。

• E3: ROCKA+DONUT+重选阈值。仍使用聚类中心曲线训练模型应用于同类其他KPI上。但在有足够标注的情况下，我们可以为每条KPI重新调优阈值来取得最佳F-score。

实验表明，相比于E1，E2的方法节省了90%的模型训练时间，且在阈值选取时几乎不需要异常标注，而异常检测的平均F-score下降不超过15%，仍能达到0.76的平均F-score。而在与E1有相同标注量的情况下采用E3的方法，平均F-score下降不超过5%。同时，在面对更大规模的KPI时，同一聚类簇中将包含更多相似曲线，从而能够节省更多的模型训练时间。

此外，作者还用两个实例说明了这种方法的有效性和合理性。处于同一聚类簇中的KPI曲线形状相似，意味着它们拥有相似的正常模式，因而能够共享同一异常检测模型。即使一些情况下由于不同曲线上异常程度不同（同一聚类簇中，有些曲线的异常是明显的尖峰，有些只是较小的异常），导致聚类中心的阈值不能很好应用于部分曲线，仍可通过重选阈值达到很好的异常检测效果。同时，异常检测模型在某些特定KPI上可能出现一定程度的过拟合，对曲线上小的波动过于敏感。利用聚类中心训练的模型将学到更少的关于特定KPI的细节，从而提升了模型的鲁棒性。

结论

本文提出了一种快速鲁棒的KPI聚类算法ROCKA，在大量KPI聚类任务中表现出很好的效果。同时，利用ROCKA辅助异常检测算法DONUT进行KPI异常检测，降低了90%的模型训练开销，且保证性能损失不超过15%。这一方法首次提出使用聚类降低大规模KPI异常检测的训练开销，使大规模KPI异常检测成为可能。

长按二维码

   

关注我们