神经网络算法：线性神经网络续

Posted 2021-04-24 猛飞的野猪

LMS算法学习率探讨

在《神经网络算法（2）》一文中，我们了解了线性神经网络的基本原理，采用LMS算法来训练网络。在线性神经网络训练中，学习率的选择非常重要，直接影响网络的性能和收敛性。下面将简要探讨确保LMS算法收敛的学习率及常见的学习率下降方式。

(1)确保网络稳定收敛的学习率

从上一篇文章可知，学习率越小，算法的运行时间越长，算法也就记忆了更多过去的数据。因此学习率的倒数反映了LMS算法的记忆容量大小。

学习率往往需要根据经验选择，且与输入向量的统计特性有关。有时我们小心翼翼的选择学习率的值，仍然有可能选择了一个过大的值，使算法难以收敛。

(2)学习率逐渐下降方式

在感知器学习算法中曾提到，学习率随着学习的进行逐渐下降比始终不变更加合理。在学习初期，用比较大的学习率保证收敛速度，随着迭代次数增加，减小学习率可以保证精度，确保收敛。

学习率常见下降方式：

线性神经网络与感知器的对比

感知器和线性神经网络在结构和学习算法上没有太大的差别，但是我们仍然能从细小的差别上找到其功能的不同点。它们的差别主要表现在网络传输函数和学习算法上。

(1)网络传输函数

LMS算法将梯度下降法用于训练线性神经网络，这个思想后来发展成反向传播法，具备可以训练多层非线性网络的能力。

感知器与线性神经网络在结构上非常相似，唯一的区别在于传输函数：感知器传输函数是一个二值阈值元件，而线性神经网络的传输函数是线性的。这就决定了感知器只能做简单的分类，而线性神经网络还可以实现拟合或逼近。

在应用中也确实如此，线性神经网络可用于线性逼近任意非线性函数，当输入与输出之间是非线性关系时，线性神经网络可以通过对网络的训练，得出线性逼近关系，这一特点可以在系统辨识或模式联想中得到应用。

(2)学习算法

学习算法要与网络的结构特点相适应。感知器的学习算法是最早提出的可收敛的算法，LMS算法与它关系密切，形式上也非常类似。它们都采用了自适应思想，这一点在后续BP神经网络中得到了进一步发展。

从表面上看，LMS算法与感知器学习算法似乎没什么两样，但二者在收敛类别上存在差别。LMS算法得到的分类边界往往处于两类模式的正中间，而感知器学习算法在刚刚能正确分类的位置就停下来了，使系统对误差更敏感。这一区别与两种神经网络的不同传输函数有关。

线性神经网络应用举例

线性神经网络只能实现线性运算，这一点与单层感知器比较类似，因此线性神经网络只能用于解决比较简单的问题。

单个线性神经网络只能解决线性可分的问题，与/或逻辑就是典型的线性可分问题，异或逻辑则线性不可分，因此需要使用上一篇文章提到的方法间接实现。

下文将以与逻辑与异或逻辑为例来简单说明线性神经网络的应用。

（1）与逻辑

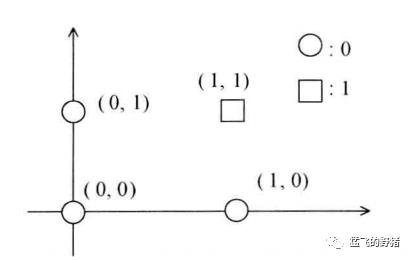
逻辑与

matlab实现如下：

%% clear

close all

clear,clc

 

%% definition

P=[0,0,1,1;0,1,0,1]       % input vector

P=[ones(1,4);P]         % input vector with offset

d=[0,0,0,1]             % desired output vector

 

% init

w=[0,0,0]              % weight vector init

lr=maxlinlr(P)          % solve the maximum learning rate 

MAX=200;            % maximum number iterations

 

%% Loop iteration

for i=1:MAX...

    fprintf('第%d次迭代\n', i);

    v=w*P;              % solve output

    y=v;

    disp('线性网络的二值输出：');

    yy=y>=0.5           % convert to a binary output with a threshold of 0.5

    e=d-y;

    m(i)=mse(e);         % Mean square error

    fprintf('均方误差： %f\n',m(i));

    dw=lr*e*P';          % The amount of weight vector adjustment

    fprintf('权值向量：\n');

    w=w+dw            % adjust the weight vector

end

 

%% display

plot([0,0,1],[0,1,0],'o');hold on;

plot(1,1,'d');

x=-2:.2:2;

y=1.5-x;

plot(x,y)

axis([-0.5,2,-0.5,2])

xlabel('x');ylabel('ylabel');

title('线性神经网络用于求解与逻辑')

legend('0','1','分类面');

 

实现结果：

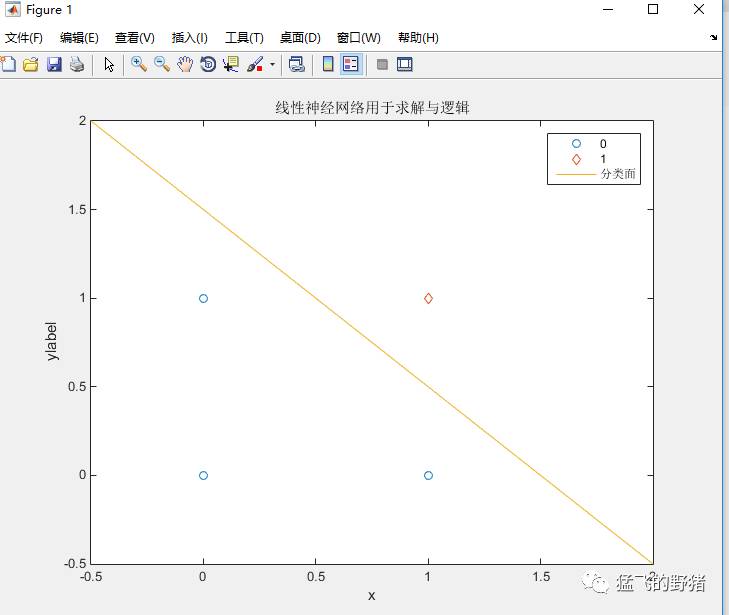
（2）异或逻辑

异或属于线性不可分问题，此处采用上一篇文章中提出的在输入端添加非线性输入的方法来实现分类，并采用MATLAB神经网络工具箱的函数来实现。

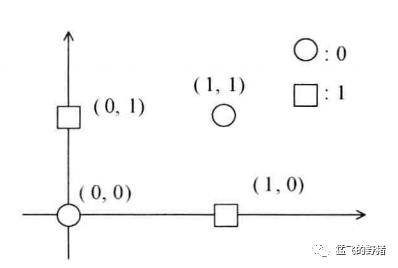
逻辑异或

添加非线性输入

matlab实现如下：

%% clear

close all

clear,clc

 

%% definition

P1=[0,0,1,1;0,1,0,1]             % input initial vector

p2=P1(1,:).^2;

p3=P1(1,:).*P1(2,:);

p4=P1(2,:).^2;

P=[P1(1,:);p2;p3;p4;P1(2,:)]   % input vector after adding the non-linear component

d=[0,1,1,0]                 % desired output vector

lr=maxlinlr(P,'bias')          % solve the maximum learning rate

 

%% Linear network implementation

net=linearlayer(0,lr);              % create linear network

net=train(net,P,d);                 % train linear network 

 

%% display

disp('网络输出')                    % command line output

Y1=sim(net,P)

disp('网络二值输出');

YY1=Y1>=0.5

disp('最终权值：')

w1=[net.iw{1,1}, net.b{1,1}]

                    

plot([0,1],[0,1],'o','LineWidth',2);    % graphics window output       

hold on;

plot([0,1],[1,0],'d','LineWidth',2);

axis([-0.1,1.1,-0.1,1.1]);

xlabel('x');ylabel('y');

title('线性神经网络用于求解异或逻辑');

x=-0.1:.1:1.1;y=-0.1:.1:1.1;

N=length(x);

X=repmat(x,1,N);

Y=repmat(y,N,1);Y=Y(:);Y=Y';

P=[X;X.^2;X.*Y;Y.^2;Y];

yy=net(P);

y1=reshape(yy,N,N);

[C,h]=contour(x,y,y1,0.5,'b');

clabel(C,h);

legend('0','1','线性神经网络分类面');

 

实现结果：

P1 =

 

     0     0     1     1

     0     1     0     1

 

P =

 

     0     0     1     1

     0     0     1     1

     0     0     0     1

     0     1     0     1

     0     1     0     1

 

d =

 

     0     1     1     0

 

lr =

 

    0.1033

 

网络输出

 

Y1 =

 

    0.0000    1.0000    1.0000    0.0000

 

网络二值输出

 

YY1 =

 

     0     1     1     0

 

最终权值：

 

w1 =

 

    0.5000    0.5000   -2.0000    0.5000    0.5000    0.0000

以上内容是上篇线性神经网络的补充，神经网络系列下篇将进入BP网络的探讨与学习。

欢迎感兴趣的朋友来信交流，[e-mail]。

———————————————

欢迎关注“猛飞的野猪”！