神经网络算法：线性神经网络算法原理

Posted 2021-04-24 猛飞的野猪

在《神经网络算法（1）》一文中，我们知道了感知器的工作原理。线性神经网络与感知器的主要区别在于，感知器的传输函数只能输出两种可能的值，而线性神经网络的输出可以取任意值，其传输函数是线性函数。

线性神经网络采用Widrow-Hoff学习规则，即LMS（Least Mean Square，最小均方误差）算法来调整网络的权值和偏置。线性神经网络在收敛的精度和速度上较感知器都有了较大的提高，但其线性运算规则决定了它只能解决线性可分的问题。

线性神经网络结构

线性神经网络在结构上与感知器网络非常相似，只是神经元传输函数不同。线性神经网络的结构如下图所示。

线性神经网络结构

由上图可知，线性神经网络除了产生二值输出以外，还可以产生连续任意输出，即采用线性传输函数，使输出可以为任意值。

若网络中包含多个神经元节点，就能形成多个输出，这种线性神经网络叫Madaline网络，其结构如下图所示。

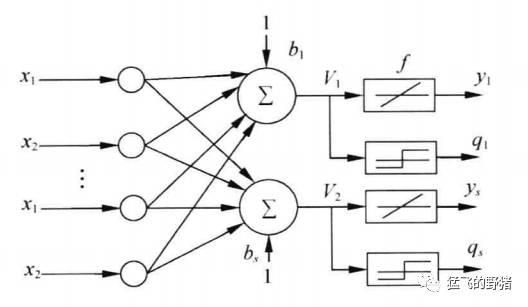
Madaline网络可以用一种间接的方式解决线性不可分问题，方法是用多个线性函数对区域进行划分，然后对各个神经元的输出做逻辑运算。

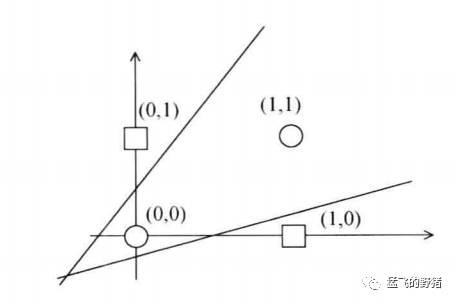
Madaline网络实现异或

线性神经网络解决线性不可分问题的另一个方法是，对神经元添加非线性输入，从而引入非线性成分，这样做会使等效的输入维度变大，结果如下图所示。

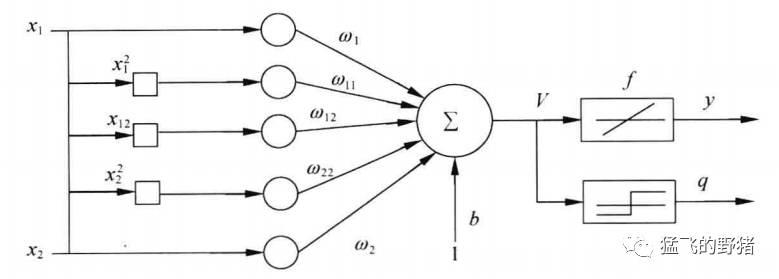
线性网络解决非线性问题

LMS学习算法

Widrow和Hoff于1960年提出自适应滤波LMS算法，也称为Delta规则（Delta Rule）。LMS算法与感知器网络的学习算法在权值调整上都基于纠错学习规则，但LMS更易实现，因此得到了广泛应用，成为自适应滤波的标准算法。

LMS算法只能训练单层网络，但这并不会对其功能造成很大影响。从理论上说，多层线性神经网络并不比单层网络更强大，它们具有同样的能力，即对于每一个多层线性网络，都具有一个等效的单层线性网络与之对应。

Q是输入训练样本的个数。线性神经网络学习的目标是找到适当的w，使得误差的均方差mse最小。只要用mse对w求偏导，再令该偏导等于零即可求出mse的极值。显然，mse必为正值，因此二次函数是凹向上的，求得的极值必为极小值。

在实际运算中，为解决权值w维数过高，给计算带来困难的问题，往往是通过调节权值，使mse从空间中的某一点开始，沿着斜面向下滑行，最终达到最小值。滑行的方向是该点最陡下降的方向，即负梯度方向。沿着此方向以适当强度对权值进行修正，就能最终达到最佳权值。

【权值更新向量推导】

至此，我们已经得到了权值更新向量公式，整个LMS算法的网络训练过程与《神经网络算法（1）：单层感知器算法原理及应用》类似，这里就不再叙述。

在这里，同样需要注意的是学习率，与感知器的学习算法类似，LMS算法也有学习率大小选择的问题，若学习率过小，则算法耗时过长，若学习率过大，则可能导致误差在某个水平上反复震荡，影响收敛稳定性。这个问题将在下文讨论。

———————————————

欢迎关注“猛飞的野猪”！