15BP神经网络算法

Posted 2021-04-24 FinTech修行僧

BP神经网络算法

神经网络有很多种：前向传输网络、反向传输网络、递归神经网络、卷积神经网络等。本文介绍基本的反向传输神经网络（Backpropagation 简称BP），主要讲述算法的基本流程和自己在训练BP神经网络的一些经验。

BP(error BackPropagation，简称BP)神经网络算法，又称反向传播算法，误差逆传播算法。

BP神经网络的结构

神经网络就是模拟人的大脑的神经单元的工作方式，但进行了很大的简化。神经网络由很多神经网络层构成，而每一层又由许多单元组成，第一层叫输入层，最后一层叫输出层，中间的各层叫隐藏层。在BP神经网络中，只有相邻的神经层的各个单元之间有联系，除了输出层外，每一层都有一个偏置结点，如下所示：

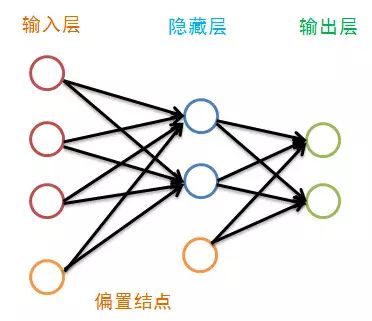
虽然图中隐藏层只画了一层，但其层数并没有限制。传统的神经网络学习经验认为一层就足够好，而最近的深度学习不这么认为。

偏置结点是为了描述训练数据中没有的特征，于是便可以认为偏置是每一个结点（除输入层外）的属性，我们将偏置bias结点在图中省略掉，如下：

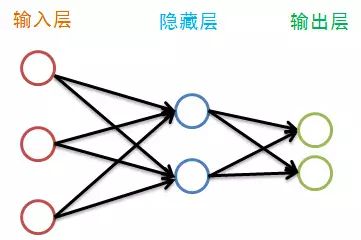
在描述BP神经网络的训练之前，我们先来看看神经网络各层都有哪些属性：

(1)每一个神经单元都有一定量的能量，我们定义其能量值为该结点j的输出值O_j；

(2)相邻层之间结点的连接有一个权重W_ij，其值在[-1,1]之间；

(3)除输入层外，每一层的各个结点都有一个输入值，其值为上一层所有结点，按权重传递过来的能量之和加上偏置bias；

(4)除输入层外，每一层都有一个偏置值bias，其值在[0,1]之间；

(5)除输入层外，每个结点的输出值等该结点的输入值作非线性变换；

(6)我们认为输入层没有输入值，其输出值即为训练数据的属性，比如一条记录X=<(1,2,3),类别1>，那么输入层的三个结点的输出值分别为1,2,3。 因此输入层的结点个数一般等于训练数据的属性个数。

训练一个BP神经网络，实际上就是调整网络的权重和偏置这两个参数，BP神经网络的训练过程分两部分：

(1)前向传输，逐层波浪式的传递输出值；

(2)逆向反馈，反向逐层调整权重和偏置；

前向传输(Feed-Forward)

在训练网络之前，我们需要随机初始化权重和偏置，对每一个权重取[-1,1]的一个随机实数，每一个偏置取[0,1]的一个随机实数，之后就开始进行前向传输。

神经网络的训练是由多趟迭代完成的，每一趟迭代都使用训练集的所有记录，而每一次训练网络只使用一条记录，抽象的描述如下：

首先设置输入层的输出值，假设属性的个数为100，那我们就设置输入层的神经单元个数为100，输入层的结点N_i为记录第 i 维上的属性值x_i 。对输入层的操作就这么简单，之后的每层就要复杂一些了，除输入层外，其他各层的输入值是上一层输入值按权重累加的结果值加上偏置，每个结点的输出值等该结点的输入值作如下变换：

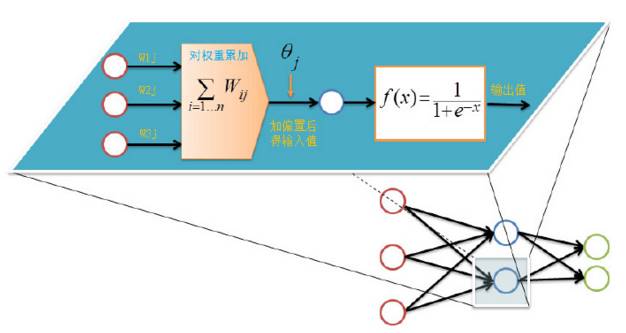
前向传输的输出层的计算过程公式如下：

                    

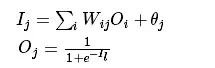
对隐藏层和输出层的每一个结点都按照如上图的方式计算输出值，就完成前向传播的过程，紧接着是进行逆向反馈。

前馈神经网络

前馈神经网络是多个感知器的组合，这些感知器以不同的方式产生连接，并由不同的激活函数控制激活，如下图示：

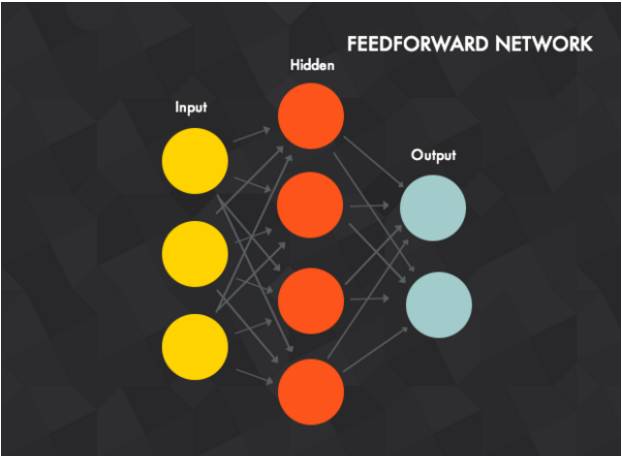
我们来认识下前馈神经网络：

(1)它包括输入层（input layer）、输出层（output layer）和一个或多个隐藏层（hidden layers）。上图的神经网络由3个单元的输入层，4个单元的隐藏层和2个单元的输出层组成。单元等于感知器。

(2)输入层的单元是隐藏层单元的输入，隐藏层单元的输出是输出层单元的输入。

(3)两个感知器之间的连接有一个权量ω。

(4)第t层的每个感知器与第t-1层的每个感知器相互关联。当然，你也可以设置权量为0，从而在实质上取消连接。

(5)在加工输入数据时，你将输入数据赋予输入层的每个单元，而隐藏层的每个单元是输入层每个单元的加权求和。也就是说，输入层的数据会被前向传播到隐藏层的每个单元。同理，隐藏层的输出作为输入会前向传播到输入层，计算得到最后的输出，即神经网络的输出。

(6)多个隐藏层的神经网络同理。

逆向反馈(BackPropagation)

逆向反馈从最后一层即输出层开始.

我们训练神经网络作分类的目的往往是，希望最后一层的输出能够描述数据记录的类别，比如对于一个二分类的问题，我们常常用两个神经单元作为输出层，如果输出层的第一个神经单元的输出值比第二个神经单元大，我们认为这个数据记录属于第一类，否则属于第二类。

在上面讲解前向传输时，整个网络的权重和偏置都是我们随机取，因此网络的输出肯定还不能描述记录的类别，因此需要调整网络的参数，即权重值ω和偏置值bias，而调整的依据就是网络的输出层的输出值与类别之间的差异，通过调整参数来缩小这个差异，这就是神经网络的优化目标。

BP算法

误差逆传播算法(err BackPropagation，简称BP)

下面我们来看看BP算法究竟是什么样。

给定训练集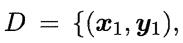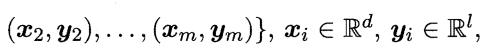即输入示例由 d 个属性描述，输出 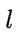维实值向量。

如下图所示，给出了一个拥有d个输入神经元、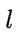个输出神经元、q个隐层神经元的多层前馈网络结构：

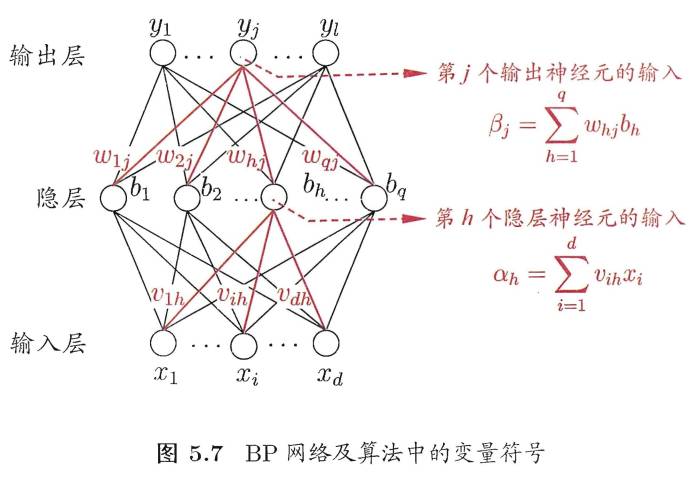
其中，输出层第 j个神经元的阈值用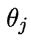表示，隐层第h个神经元的阈值用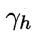表示。

输入层第 i 个神经元与隐层第h 个神经元之间的连接权为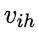，隐层第h个神经元与输出层第j个神经元之间的连接权为。

记隐层第h个神经元接收到的输入为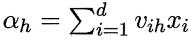

输出层第j个神经元接收到的输入为

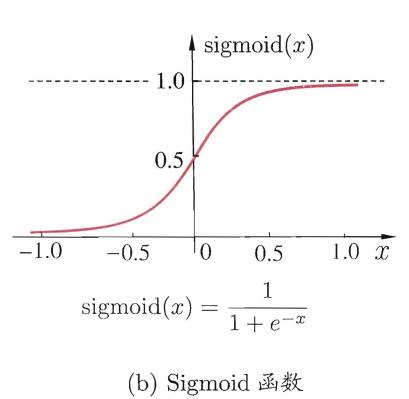
，其中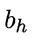为隐层第h个神经元的输出。假设隐层和输出层神经元都使用如下图中的Sigmoid函数。

对训练实例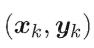，假定神经网络的输出为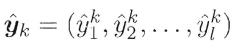，即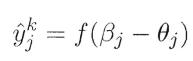

则网络在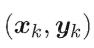上的均方误差为：

            

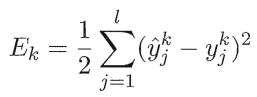
注：这里的1/2是为了后续求导的便利。

上图中共有(d+L+1)q+L个参数需确定：输入层到隐层的d*q个权值，隐层到输出层的q*L个权值，q个隐层神经元的阈值，L个输出层神经元的阈值。

BP算法是一个迭代学习算法，在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计，任意参数 v 的更新估计式为：

                    

下面我们以上图中隐层到输出层的连接权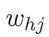为例来进行推导：

BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，对误差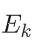，给定学习率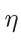，有

                    

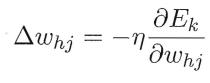
我们注意到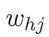先影响到第 j 个输出层神经元的输入值β_j，再影响到其输出值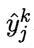，然后影响到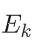，有

                 

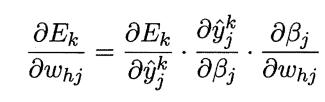
这是根据链式求导法则。

根据β_j的定义，显然有

                    

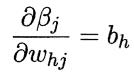
由于Sigmoid函数的导数有一个很好的性质：

                    

于是联立上述式子有：

                    

进而，我们可以得到BP算法中关于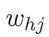的更新公式：

                    

类似的，我们根据已知的关系式，如下：

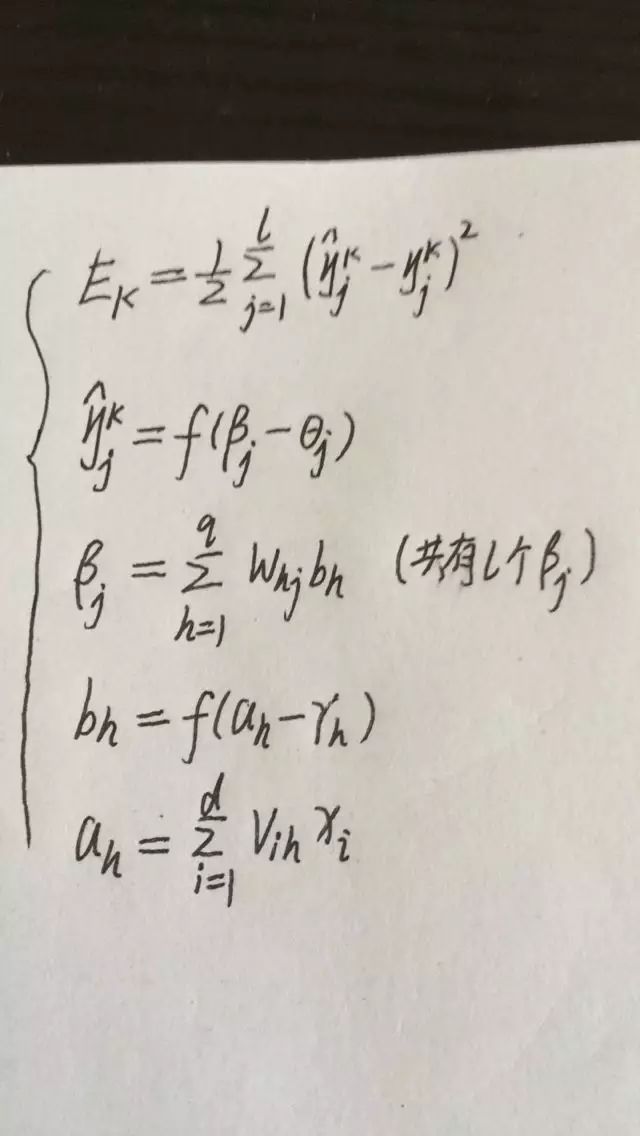
可得：

                    

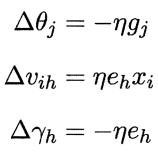
上式中：

              

                    

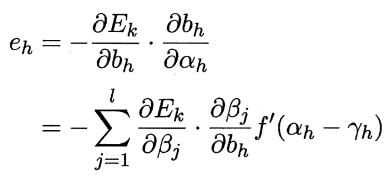
学习率η∈(0，1)控制着算法每一轮迭代中的更新步长，若太大则容易振荡，太小则收敛速度又会过慢，常设置η=0.1 。

BP误差逆传播算法流程

标准BP算法

标准BP算法工作流程解释如下：

对每个训练样例，BP算法执行如下操作：先将输入示例提供给输入层神经元，然后逐层将信号前传，直到产生输出层的结果；然后计算输出层的误差(第4-5行)，再将误差逆向传播至隐层神经元(第6行)，最后根据隐层神经元的误差来对连接权和阈值进行调整(第7行)。该迭代过程循环进行，直到达到某些停止条件为止，例如训练误差已达到一个很小的值。

需要注意的是，BP算法的目标是要最小化训练集D上的累积误差(训练集误差之和)：

                

但是我们上面介绍的“标准BP算法”每次仅针对一个训练样例更新连接权ω和阈值。也就是说，图5.8算法更新规则是基于单个的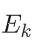推导而得。

累积BP算法(accumulated error backpropagation)

我们可以依据标准BP算法推导出累积误差最小化的更新规则，便得到了累积误差逆传播算法。

标准BP算法与累积BP算法的对比

标准BP算法每次更新只针对单个样例，参数更新得非常频繁，而且对不同样例进行更新的效果可能出现“抵消”现象。因此，为了达到同样的累积误差极小点，标准BP算法往往需要进行更多次数的迭代。

累积BP算法直接针对累积误差最小化，它在读取整个训练集D一遍后才对参数进行更新，其参数更新的频率低得多。但在很多任务中，累积误差下降到一定程度之后，进一步下降会非常缓慢，这时标准BP算法往往会更快获得较好的解，尤其是在训练集D非常大时更明显。

标准BP算法与累积BP算法的区别类似于随机梯度下降与标准梯度下降。

如何缓解BP网络的过拟合?

BP神经网络经常遭遇过拟合，其训练误差持续降低，但测试误差却可能上升，有两种策略常用来缓解BP网络的过拟合：

第一种策略是“早停”(early stopping)

将数据分成训练集和验证集，训练集用来计算梯度、更新连接权ω和阈值；验证集用来估计误差，若训练误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值；

第二种策略是“正则化”(regularization)

基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分，例如连接权和阈值的平方和。仍令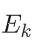表示第 k 个训练样例上的误差，ω_i表示连接权和阈值，则误差目标函数变为：

       

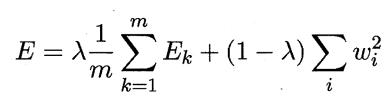
其中，λ∈(0,1)用于对经验误差与网络复杂度这两项进行折中，常通过交叉验证法来估计。

注：增加连接权与阈值平方和这一项后，训练过程将会偏好比较小的连接权和阈值，使网络输出更加“光滑”，从而对过拟合有所缓解。

如何跳出局部最小点，进而逼近全局最小点？

在现实任务中，人们常采用以下策略来试图“跳出”局部极小，从而进一步接近全局最小：

(1)以多组不同参数值初始化多个神经网络，按标准方法训练后，取其中误差最小的解作为最终参数。

这相当于从多个不同的初始点开始搜索，这样就可能陷入不同的局部极小，从中进行选择有可能获得更接近全局最小的结果。

(2)使用“模拟退火”技术(simulated annealing)

模拟退火在每一步都以一定的概率接受比当前解更差的结果，从而有助于“跳出”局部极小。在每步迭代过程中，接受“次优解”的概率要随着时间的推移而逐渐降低，从而保证算法稳定。

(3)使用随机梯度下降SGD

与标准梯度下降法精确计算梯度不同，随机梯度下降法在计算梯度时加入了随机因素。于是，即便陷入局部极小点，它计算出的梯度仍可能不为0，这样就有机会跳出局部极小继续搜索。

(4)使用遗传算法(genetic algorithms)

总之，上述跳出局部极小的技术大多是启发式，理论上尚缺乏保障。

训练终止条件

每一轮训练都使用数据集的所有记录，但什么时候停止呢？

停止条件有下面两种：

(1)设置最大迭代次数，比如使用数据集迭代100次后停止训练;

(2)计算训练集在网络上的预测准确率，达到一定门限值后停止训练;

训练BP神经网络的一些经验

讲一下自己训练神经网络的一点经验：

(1)学习速率不宜设置过大，一般小于0.1，开始我设置了0.85，准确率一直提不上去，很明显是陷入了局部最优解；

(2)输入数据应该归一化；

(3)尽量是数据记录随机分布，不要将数据集按记录排序。

假设数据集有10个类别，我们把数据集按类别排序，一条一条记录地训练神经网络，训练到后面，模型将只记得最近训练的类别而忘记了之前训练的类别；

(4)对于多分类问题，比如汉字识别问题，常用汉字就有7000多个，也就是说有7000个类别，如果我们将输出层设置为7000个结点，那计算量将非常大，并且参数过多而不容易收敛，这时候我们应该对类别进行编码，7000个汉字只需要13个二进制位即可表示，因此我们的输出成只需要设置13个结点即可。

参考文献

【1】周志华 · 机器学习 · 清华大学出版社 · 第五章

【2】BP神经网络算法与实践 http://blog.jobbole.com/90184/

【3】如何简单形象又简单有趣地讲解神经网络是什么 ？ https://www.zhihu.com/question/22553761  舒小曼回复