算法第6期|神经网络算法基本结构与建模

Posted 2021-04-24 金风功率预测员工版

一、神经网络构成

机器学习离不开神经网络算法，它是其中的一种监督学习算法（有特征，有目标）。一个完整的神经网络预测算法，需要很多函数组成。如下图是一个tflearn神经网络预测算法由不同的函数构成一个完整的神经网络算法。

一个完整的神经网络，需要许多神经元构成输入层，隐含层、输出层，再加上不同的优化器函数，激活函数，损失函数，再加上不同的超参（迭代次数、每次训练数据长度等）组成。

神经元

神经网络算法由一个个神经元组成，神经元类似我们脑细胞中的神经元

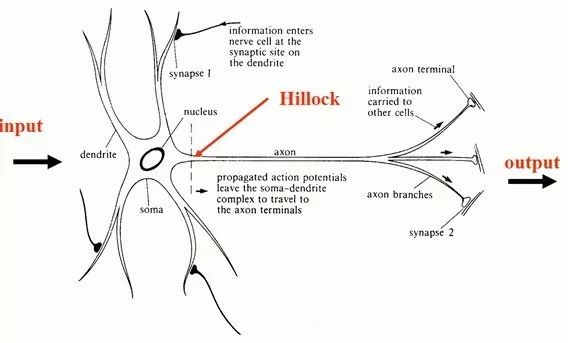
下图为单个神经元的数学模型，可以看出它是人脑神经元的简化 

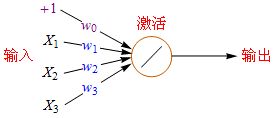
一个数学模型的神经元包括:  +1代表偏移值(偏置项, Bias Units)；X1,X2,X2代表初始特征；w0,w1,w2,w3代表权重(Weight),举例说明

输入层、隐含层、输出层

人脑是由许许多多的神经元组成的，人工神经网络也类似人脑一样，许许多多的神经元构成了神经网络结构。每一个神经网络都由输入层、隐含层和输出层组成，不同层数、节点数据构成不同深度的神经网络。如下图举例不同输入层、隐含层、输出层组成的神经网络

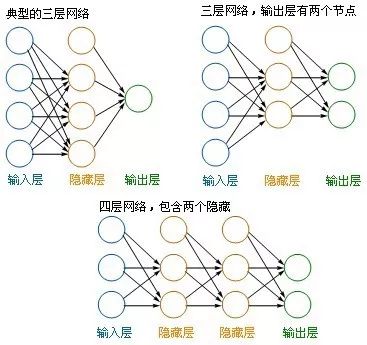
- 左边蓝色的圆圈叫“输入层”，中间橙色的不管有多少层都叫“隐藏层”，右边绿色的是“输出层”。

- 每个圆圈，都代表一个神经元，也叫节点(Node)。

- 输出层可以有多个节点

- 理论证明，任何多层网络可以用三层网络近似地表示。 一般凭经验来确定隐藏层到底应该有多少个节点，在测试的过程中也可以不断调整节点数以取得最佳效果。

激活函数

上面激活函数y=x/5是线性的，只能拟合线性的预测模型；为了拟合非线性模型，神经网络最常见的激活函数是Sigmoid(S形曲线)，双曲正切函数(tanh)和rulu。三种激活函数如下图：

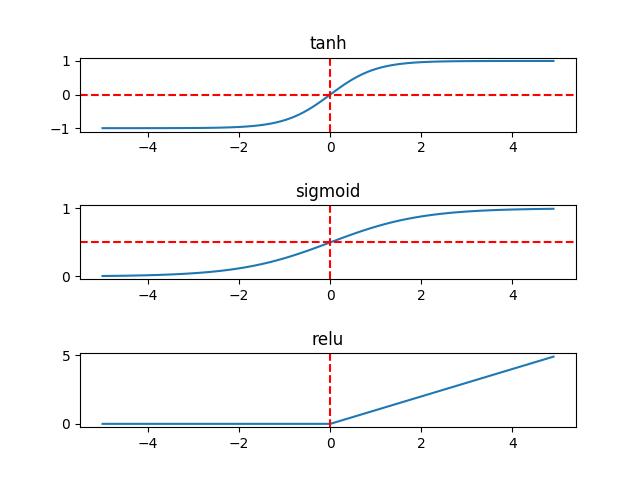
Sigmoid有时也称为逻辑回归(Logistic Regression)，简称logsig。logsig曲线的公式如下：

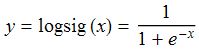
还有一种S形曲线也很常见到，叫双曲正切函数(tanh)，或称tansig，可以替代logsig。

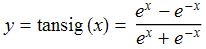
下面是它们的函数图形，从图中可以看出logsig的数值范围是0~1，而tansig的数值范围是-1~1。

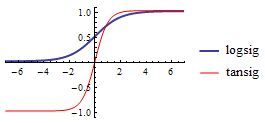
在深度学习神经网络经常用到rulu激活函数，relu函数定义为 y = max(0, x)。

优化器

 1、随机梯度下降(SGD)

随机梯度下降（Stochastic gradient descent，SGD）对每个训练样本进行参数更新，每次执行都进行一次更新，且执行速度更快。

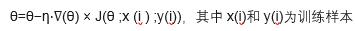
随机梯度下降算法每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的，并且可以进行在线更新。随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进行，可能是局部最优解，而不是全局最优解。如下图

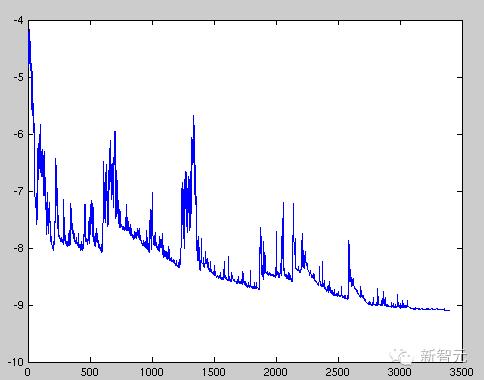
不过从另一个方面来看，随机梯度下降所带来的波动有个好处就是，对于类似盆地区域（即很多局部极小值点）那么这个波动的特点可能会使得优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点，这样便可能对于非凸函数，最终收敛于一个较好的局部极值点，甚至全局极值点。由于波动，因此会使得迭代次数（学习次数）增多，即收敛速度变慢。不过最终其会和全量梯度下降算法一样，具有相同的收敛性，即凸函数收敛于全局极值点，非凸损失函数收敛于局部极值点。

2、Momentum

通常情况我们在训练深度神经网络的时候把数据拆解成一小批一小批地进行训练，这就是我们常用的mini-batch SGD训练算法，然而虽然这种算法能够带来很好的训练速度，但是在到达最优点的时候并不能够总是真正到达最优点，而是在最优点附近徘徊。另一个缺点就是这种算法需要我们挑选一个合适的学习率，当我们采用小的学习率的时候，会导致网络在训练的时候收敛太慢；当我们采用大的学习率的时候，会导致在训练过程中优化的幅度跳过函数的范围，也就是可能跳过最优点。我们所希望的仅仅是网络在优化的时候网络的损失函数有一个很好的收敛速度同时又不至于摆动幅度太大。所以Momentum优化器刚好可以解决我们所面临的问题，它主要是基于梯度的移动指数加权平均

3、RMSProp

RMSProp算法的全称叫 Root Mean Square Prop，是Geoffrey E. Hinton在Coursera课程中提出的一种优化算法，初步解决了优化中摆动幅度大的问题。

如下图所示，蓝色的为Momentum优化算法所走的路线，绿色的为RMSProp优化算法所走的路线

4. Adam

Adaptive Moment Estimation (Adam) 也是一种不同参数自适应不同学习速率方法，与Adadelta与RMSprop区别在于，它计算历史梯度衰减方式不同，不使用历史平方衰减，其衰减方式类似动量。Momentum和RMSProp两种优化算法，一种可以使用类似于物理中的动量来累积梯度，另一种可以使得收敛速度更快同时使得波动的幅度更小。Adam(Adaptive Moment Estimation）算法是将Momentum算法和RMSProp算法结合起来使用的一种算法，在训练的最开始我们需要初始化梯度的累积量和平方累积量。Adam这种优化器比Momentum和RMSProp又有了进一步的好表现。

5、优化器选择

下面两幅图可视化形象地比较上述各优化方法

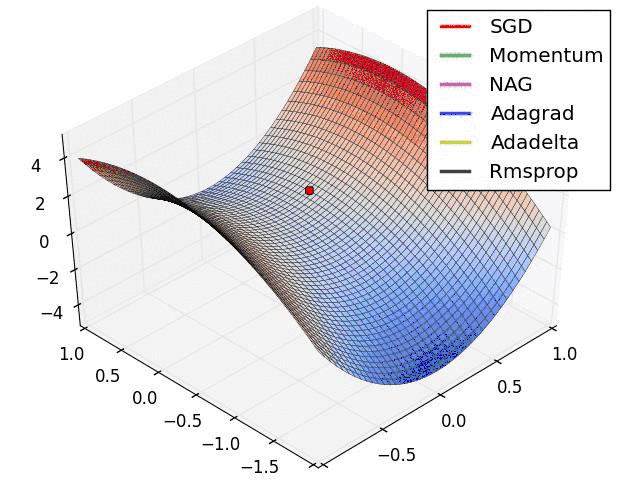
SGD各优化方法在损失曲面上的表现

上图可以看出， Adagrad、Adadelta与RMSprop在损失曲面上能够立即转移到正确的移动方向上达到快速的收敛。而Momentum 与NAG会导致偏离(off-track)。同时NAG能够在偏离之后快速修正其路线，因为其根据梯度修正来提高响应性。

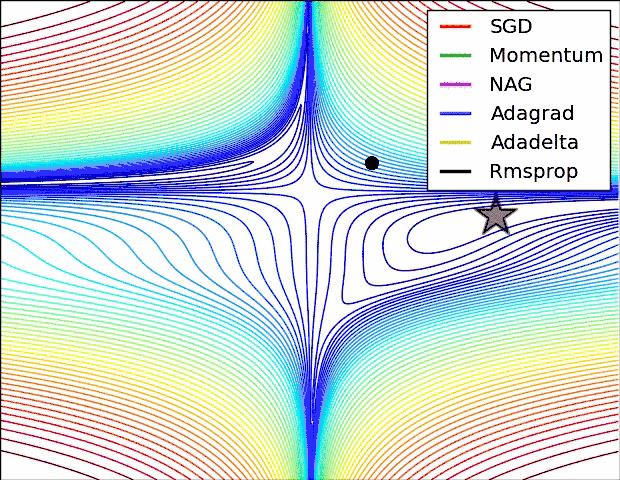
SGD各优化方法在损失曲面鞍点处上的表现

从上图可以看出，在鞍点（saddle points）处(即某些维度上梯度为零，某些维度上梯度不为零)，SGD、Momentum与NAG一直在鞍点梯度为零的方向上振荡，很难打破鞍点位置的对称性；Adagrad、RMSprop与Adadelta能够很快地向梯度不为零的方向上转移。

如果你的数据特征是稀疏的，那么你最好使用自适应学习速率SGD优化方法(Adagrad、Adadelta、RMSprop与Adam)，因为你不需要在迭代过程中对学习速率进行人工调整。RMSprop是Adagrad的一种扩展，与Adadelta类似，但是改进版的Adadelta使用RMS去自动更新学习速率，并且不需要设置初始学习速率。而Adam是在RMSprop基础上使用动量与偏差修正。RMSprop、Adadelta与Adam在类似的情形下的表现差不多。Kingma[15]指出收益于偏差修正，Adam略优于RMSprop，因为其在接近收敛时梯度变得更加稀疏。因此，Adam可能是目前最好的SGD优化方法。

损失函数

损失函数，即我们常说的loss，是计算一个样本的误差。常见的损失函数有 MSE均方误差损失函数、SVM合页损失函数、Cross Entropy交叉熵损失函数等。一般的神经网络都可以自定义损失函数，比如要求预测值与实际值之间均方根误差最小，那么使用MSE做为激活函数；比如要求积分电量考核分最小，我们可以按照西北两个细则考核分计算公式自定义激活函数。

如定义一个根据西北两个细则的tflearn的损失函数

二、BP神经网络建模

建模都需要经历以下三步

1、 对样本数据归一化

2、 设置模型参数，建立模型

3、 保持模型

以下是第二步，建立模型时，每迭代一次更新模型weight和bias的步骤

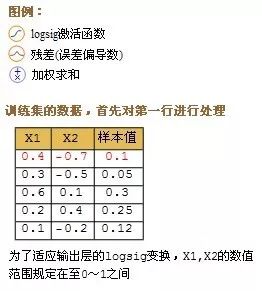
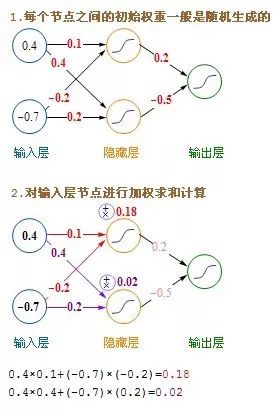
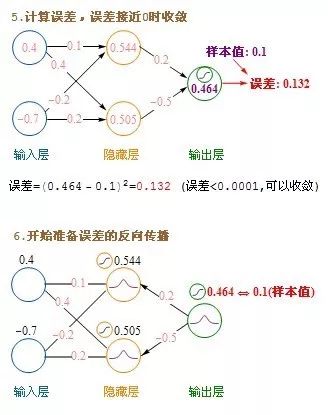
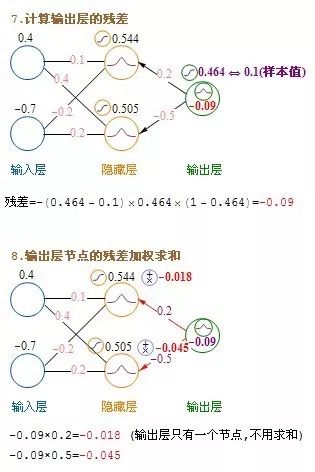
这里介绍的是计算完一条记录，就马上更新权重，以后每计算完一条都即时更新权重。方法是在不更新权重的情况下，把记录集的每条记录都算过一遍，把要更新的增值全部累加起来求平均值，然后利用这个平均值来更新一次权重，然后利用更新后的权重进行下一轮的计算，这种方法叫批量梯度下降(Batch Gradient Descent)。

三、神经网络算法优点

1、 可以多特征输入，多输出

2、 使用深度学习神经网络，正则化、dropout和bath_size等超参可以防止过拟合

3、修改超参灵活，可修改优化器、激活函数，损失函数，dropout、bath_size，使精度达到最优。