神经网络算法基础——AI入门第12讲

Posted 2021-04-24 九牂

这门AI入门课程的视频来自网易公开课，由MIT的Winston教授录制。

 

https://open.163.com/newview/movie/free?pid=MCTMNN3UI&mid=MCTMOTSCG

 

第12课时：机器学习——神经网络、反向传播

 

1     对神经网络建模

 

右边是轴突，只有一个轴突。左边是树突，有很多。突触指的是两个神经元之间相互接触并传递信号的部位。树突和很多其他神经元的轴突连接在一起。A的轴突会向B的树突传递兴奋。当树突积累了足够的兴奋之后，就会产生一个尖峰信号，该信号沿着轴突往下传播。

 

需要注意，神经网络一定同时包含以下三个特征：

1）存在突触，有些突触更加重要，所以有突触权重的概念。

2）积累效应，树突需要积累刺激，并决定是否需要传播尖峰信号。

3）要么传播，要么不传播

分别对应到→

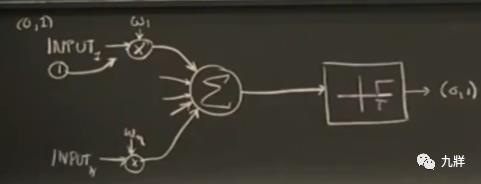
1）输入进入一个乘法函数，乘以一个权重。

2）对权重和输入之积进行求和，也就是传给一个求和函数。

3）输出并不正比于输入，要么有要么无，也就是将相加和送入一个临界值函数。输出要么是0，要么是1。

 

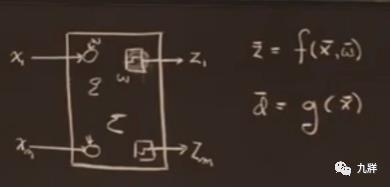
用很多这样的神经元模型组成一个神经网络模型。输出向量z是输入向量x和权重向量w的f函数。实际上f还依赖于神经网络的结构，因为结构固定，所以不去考虑结构。

 

如果有训练样本（比如标记过的小狗照片），可以调整这个神经网络，使得，对特定输入（比如新的小狗图片）得到理想输出（判定为狗）。

 

理想输出d（此时不关心权重）是输入x的g函数。希望让f函数和g函数对上，也就是希望有一系列调整过的权重，让实际输出等于想要的输出。

 

2     设立性能函数p

 

需要衡量权重向量的好坏，权重向量是理想输出和实际输出的某个函数，设为性能函数p。

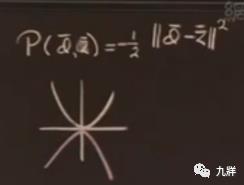
为了数学便利才这么设计，并没有理论根据。求解性能函数的最大值就可以，因为p只能为负的，所以越接近于0说明理想输出和实际输出的差异越小。求解最大值，就可以转换为爬山问题。

考虑只有两个权重的情况，这些圈圈是性能函数的等高线，想象成是一个三维图形。假设最开始的一组w1和w2值是由随机数生成器生成的，在最下面的一个圈上。典型的爬山问题，只有两个维度，那么就是东西南北四个方向，这里似乎朝东爬是最好的。但是如果有很多w，这里的维度就会变得很高，就是2的n次方个方向，如果还是尝试每个方向就不明智了。

 

3  处理技巧

 

1）便捷考虑临界值函数

原本，我们需要先考虑权重，再考虑临界函数。通过一个小转换，可以将权重和临界函数同时考虑。

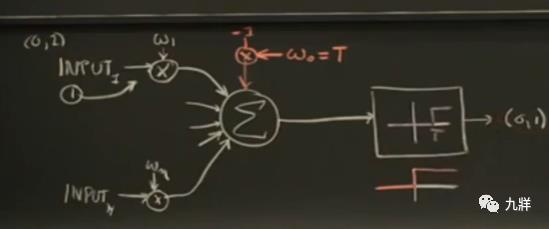
在累加器这里额外增加一个输入，值为-1，权重为T（临界值）。这样就相当于把T减掉了，触发发生在0而不是T。并且，临界值转为权重之后，可以和其他权重一起处理。

 

2）选择正确的爬山方向

不是呆萌地沿着东西南北等方向爬，而是沿着垂直于等高线的方向爬，梯度上升法。r是速率常数。△w是一个向量，指出w1和w2的调整方案。但是，有一个问题，使用梯度上升法的前提是函数曲线平滑连续，而这个是阶跃函数。之前讲到，临界函数要么输出0要么输出1，不会输出0.5。

 

3）平滑处理阶跃函数

做一个近似调整，让临界函数不要这么尖锐，在经过0的时候平滑一些，在两端则是保持不变。

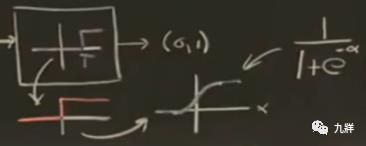
选用这个S型函数，是因为数学便利性。

 

4 最简单的神经网络公式模型

 

这里只有一个维度，所以写作标量而不是向量。假设有一些样本x，有初始化的w，有理想的输出值d，可以观察实际值z。以让实际输出靠近理想输出为目标（只能让p函数尽量趋近于零），进行偏导计算，对权重进行调整。有初始的w，调整需要方向和步长。方向由偏导的计算结果决定，看看依赖于哪些变量。步长自己设定。在给定有限的样本情况下，训练出最好的w，最好的神经网络模型。

求偏导，简化到只需要求出临界函数的导数。

因为数学便利性选择S函数，这里体现出了便利性，让输出对输入的导数可以用输出本身来表示。

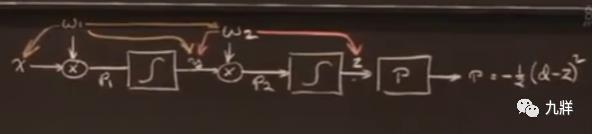
对p进行w2的偏导，结果只依赖于y和z，对p进行w1的偏导，结果只依赖于w2、x、y。带入到△w之后，知道了w1和w2该如何调整。也就是说，w1和w2只依赖于x、y、z。

 

5 反向传播算法

 

假设有100个上面这样的神经网络模型，排成一长串。最后一个模型只依赖于已经算过的东西和相邻的东西，而不是依赖于之前的99个。

 

先计算出离输出最近的w，再反向推出前一个w，再前一个w，一直回到最开始。每一个w的计算量是相同的，这是一种局部计算。

 

6 几点注意事项

 

1）这种技术实际上是在做什么？

它有一些理想输出，然后设法得到一些实际输出，让其类似于理想输出。神经网络其实就是曲线拟合。调整系统，使得系统输出的离散点尽量拟合出一条完美的曲线。不过这比傅里叶变换要好。

2）实际解决问题时难在哪里？

如果有一个赛马相关的问题，如何将参数编码到输入向量中以反映出问题的实质，通常这是最难的部分。

3）过度拟合

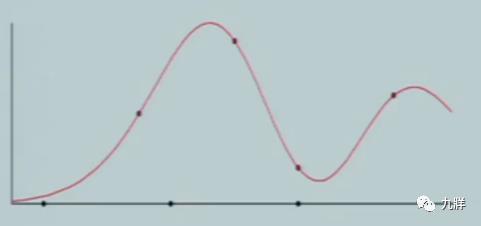
有一些离散点，有一条完美红曲线，希望用这些离散点构建出一个曲线，来贴近完美红曲线。

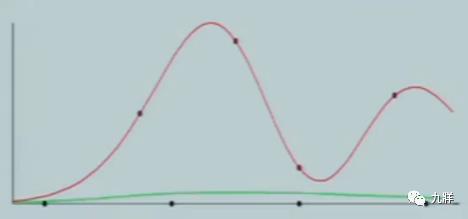
最开始是一条绿色曲线，逐步贴近。

为了逼近，这条曲线开始疯狂弯曲，这就是过度拟合。为了匹配样本点，曲线过分扭曲了。特点是附近的值通常会被高度扭曲。

4）选择调整速率常数r

之前一次走一步，拟合太慢，现在一次走100步。因为要根据p函数来不断调整w，所以这里有一个正反馈回路。速率太高了 ，开始振荡，自己爆掉。因此需要选择调整速率常数，避免这种猛烈的正反馈情形，这种情况下无法收敛到答案。