第20集 python机器学习：神经网络算法

Posted 2021-04-24 AI学习小帮手

神经网络算法最近似“深度学习”，不过尽管深度学习在许多机器学习应用中具有巨大的潜力，但是由于深度学习算法往往经过精度调整，一般只适用于特定的应用场景。由于目前我们还未学习较为高深的算法，所以目前我们暂时只讨论一些相对简单的方法，即用于分类和回归的多层感知机（MLP，也被称为前馈神经网络或神经网络），可以将其作为研究深度复杂的深度学习方法的起点。

神经网络模型：MLP可以被视为广义的线性模型，在执行多层处理后得到结论，线性模型的预测公式为：y = w[0]*x[0] + w[1]*x[1] + ...+w[p]*x[p] + b (其中，y是输入特征项x[0]到x[p]的加权求和，权重为学到系数w[0]到w[p]。我们可以将这个公式可视化，如下图所示：

from IPython.display import display

display(mglearn.plots.plot_logistic_regression_graph())

Logistic回归可视化，其中输入特征和预测结果显示为结点，系数是结点之间的连线

图中，左边的每个结点代表一个输入特征，连线代表学到的系数，右边的结点代表输出，是输入的加权求和。在MLP中，对此重复这个过程计算加权求和的过程，首先计算代表中间的隐藏单元，然后再计算这些隐藏单元的加权求和并得到最终结果。单隐层的多感知机如下图所示：

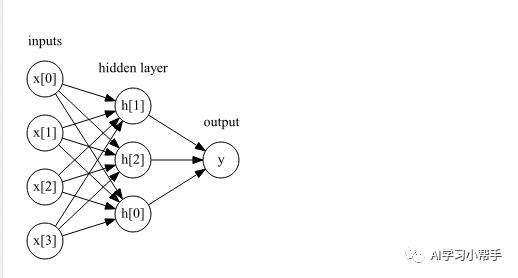单隐层多感知机图示

这个模型需要学习更多的系数（也叫作权重）：在每个输入与每个隐藏单元（隐藏单元组成了一个隐藏层）之间有一个系数，在每个隐藏单元与输出之间也有一个系数。

从数学的角度来看，计算一系列加权求和与只计算一个加权求和是一样的。因此，为了让这个模型比线性模型更加强大，我们还需要在计算完每个隐藏单元的加权求和之后，对结果再应用一个非线性函数（通常为校正非线性或叫校正线性单元或relu）或正切双曲线。然后将这个函数的结果加权求和，计算得到输出y。可通过如下示例来进行说明：

代码内容如下：

import matplotlib.pyplot as plt

line = np.linspace(-4, 4, 100)

plt.plot(line, np.tanh(line), label="tanh")

plt.plot(line, np.maximum(line, 0), label="relu")

plt.legend(loc="best")

plt.xlabel("x value")

plt.ylabel("relu(x) value, tanh(x) value")

运行后结果如图：

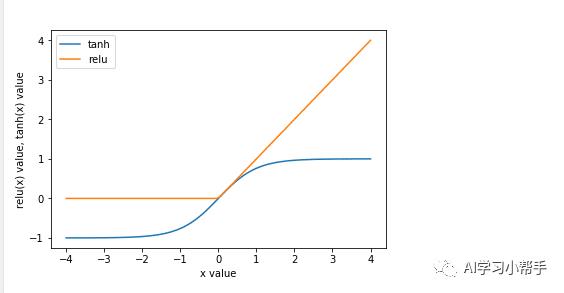双曲正切激活函数与校正线性激活函数

其中，relu截断小于0的值，而tanh输入值较小时接近-1，在输入值较大时接近+1.有了这两种非线性函数，神经网络可以学习比线性模型复杂得多的函数。

计算回归问题的y的完整公式如下（使用tan非线性）：

h[0] = tanh(w[0,0]*x[0] + w[1,0]*x[1] +w[2,0]*x[2] + w[3,0]*x[3] +w[4,0]*x[4] +b[0])

h[0] = tanh(w[0,0]*x[0] + w[1,0]*x[1] +w[2,0]*x[2] + w[3,0]*x[3] +w[4,0]*x[4] +b[1])

h[0] = tanh(w[0,0]*x[0] + w[1,0]*x[1] +w[2,0]*x[2] + w[3,0]*x[3] +w[4,0]*x[4] +b[2])

h[0] = tanh(w[0,0]*x[0] + w[1,0]*x[1] +w[2,0]*x[2] + w[3,0]*x[3] +w[4,0]*x[4] +b[3])

y = v[0]*h[0] + v[1]*h[1] + v[2]*h[2] + b

其中，w是输入x与隐藏层h之间的权重，v是隐藏层h与输出y之间的权重。权重w和v需要在数据学习中得到，是x的输入特征，y是计算得到的输出，h是计算的中间结果。需要用户设置的一个重要参数是隐藏层中的节点个数。对于非常小或非常简单的数据集。这个值可以小到10，对于非常复杂的数据，这个值可以达到10000.也可以添加多个隐藏层，如下图所示：

display(mglearn.plots.plot_two_hidden_layer_graph())

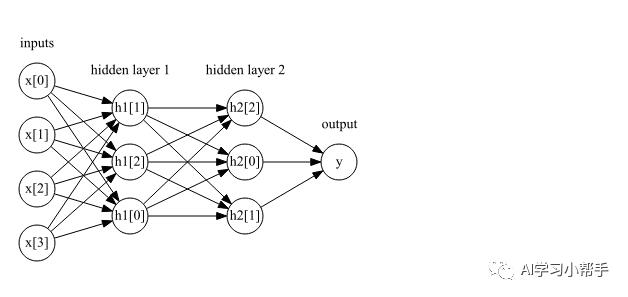含有两个隐藏层的感知机

神经网络参数调整：我们将MLPClassifier应用到two_moons数据集上，以此来讨论MLP的工作原理，对应的代码内容如下：

from sklearn.neural_network import MLPClassifier

from sklearn.datasets import make_moons

x, y = make_moons(n_samples=100, noise=0.25, random_state=3)

x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y, random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(x_train, y_train)

mglearn.plots.plot_2d_separator(mlp, x_train, fill=True, alpha=.3)

mglearn.discrete_scatter(x_train[:, 0], x_train[:, 1], y_train)

plt.xlabel("Feature 0 value")

plt.ylabel("Feature 1 value")

运行后结果如下：

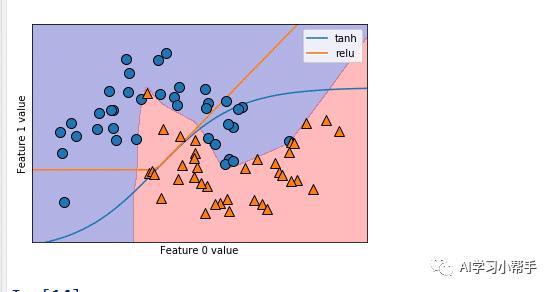包含100个隐藏单元的神经网络在two_moons数据集上学到的决策边界

从运行结果可知，神经网络学习到的决策边界完全是非线性的，但相对平滑，默认情况下，MLP使用100个隐藏结点，这对于这个小型数据及来说已经很多了，我们也可以适当降低隐藏结点的数量，如下：

from sklearn.neural_network import MLPClassifier

from sklearn.datasets import make_moons

x, y = make_moons(n_samples=100, noise=0.25, random_state=3)

x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y, random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[15]).fit(x_train, y_train)

mglearn.plots.plot_2d_separator(mlp, x_train, fill=True, alpha=.3)

mglearn.discrete_scatter(x_train[:, 0], x_train[:, 1], y_train)

plt.xlabel("Feature 0 value")

plt.ylabel("Feature 1 value")

运行后结果为：

包含15个隐藏结点的神经网络在two_moons数据集上学到的决策边界

从上述的运行结果来看，将隐藏结点修改为15个时，边界看起来会更加参差不齐。不过效果仍然不错，下面我们来看使用双隐藏层的效果，对应代码如下：

#使用双隐藏层的代码

mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[15,15]).fit(x_train, y_train)

mglearn.plots.plot_2d_separator(mlp, x_train, fill=True, alpha=.3)

mglearn.discrete_scatter(x_train[:, 0], x_train[:, 1], y_train)

plt.xlabel("Feature 0 value")

plt.ylabel("Feature 1 value")

运行后结果如下：

包含两个隐藏层，含有15个隐藏单元的神经网络决策边界 （激活函数为relu）

下面我们再来看使用双隐藏层，也是含有15个隐藏单元，但是激活函数为tanh的代码及运行结果：

mlp = MLPClassifier(solver='lbfgs', random_state=0,

activation='tanh',hidden_layer_sizes=[15,15]).fit(x_train, y_train)

mglearn.plots.plot_2d_separator(mlp, x_train, fill=True, alpha=.3)

mglearn.discrete_scatter(x_train[:, 0], x_train[:, 1], y_train)

plt.xlabel("Feature 0 value")

plt.ylabel("Feature 1 value")

运行结果如下：

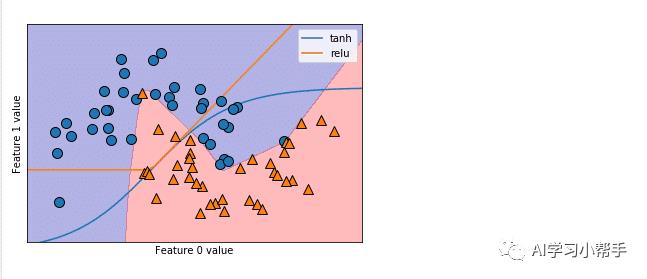
当激活函数为tanh的运行结果

通过上面的运行结果可以知道，当隐藏结点增加或者隐藏层数增多时，我们得到的决策边界就越光滑，效果就越好，模型也就越复杂。

关于神经网络算法的内容暂时介绍到这里，如果有什么疑问或建议可以留言讨论，祝大家生活愉快！喜欢就请关注我吧！