模拟LeetCode 54. 螺旋矩阵
Posted 书所集录
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了模拟LeetCode 54. 螺旋矩阵相关的知识,希望对你有一定的参考价值。
2021 第 28 篇题解
54. 螺旋矩阵
题目来源:力扣(LeetCode)https://leetcode-cn.com/problems/spiral-matrix/
题目
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
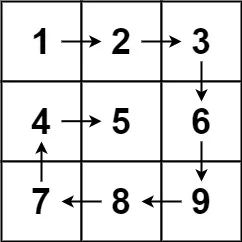
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
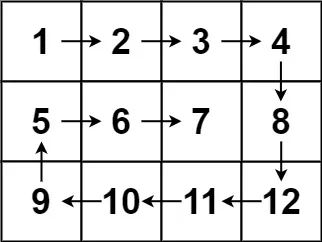
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
-
m == matrix.length -
n == matrix[i].length -
1 <= m, n <= 10 -
-100 <= matrix[i][j] <= 100
解题思路
思路:模拟
先审题,题目给定一个 的矩阵 ,
题目要求:
-
按照 顺时针螺旋顺序,返回矩阵中的所有元素。
这里,以示例 1,
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]

以上图示出处:力扣
用动图的形式看下其中过程:
从图中,我们可以发现的信息:
-
起始点在矩阵的左上角; -
题目中所述 顺时针螺旋顺序,分解后即是按照 右、下、左、上 的顺序循环移动; -
遇到边界或者其中元素被访问过时,方向会发生改变。 -
移动停止的标志,是当所有的元素都被访问完毕。
那么根据上面所得的信息,制定对应的策略:
-
定义变量 存储四个方向,分别对应 右、下、左、上; -
定义 的二维数组 ,用以标记元素是否已访问; -
起始位置为矩阵左上角,初始方向 向右,开始遍历数组; -
当移动过程中,遇到边界或者下一个元素已经被访问过时,改变方向(其中,这里的方向对应 中方向顺序循环变化) -
当移动路径的长度等于元素个数时,移动停止。
具体的代码实现如下:
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m = len(matrix)
n = len(matrix[0])
prod = m * n
# 标记是否访问
visited = [[False] * n for _ in range(m)]
ans = [0] * prod
# 四个方向,分别是 右、下、左、上
directions = [[0, 1], [1, 0], [0, -1], [-1, 0]]
x = 0
y = 0
# directions 中对应的索引,用以表示往某个方向
idx = 0
# 开始遍历
for i in range(prod):
ans[i] = matrix[x][y]
visited[x][y] = True
nx = x + directions[idx][0]
ny = y + directions[idx][1]
# 越界或已访问,改变方向
if nx < 0 or nx >= m or ny < 0 or ny >= n or visited[nx][ny]:
idx = (idx + 1) % 4
# 往改变后的方向移动
x += directions[idx][0]
y += directions[idx][1]
return ans
复杂度分析
-
时间复杂度: , 是矩阵的行数, 是矩阵的列数。 -
空间复杂度: ,除返回数组外,需要声明 的二维数组标记元素是否被访问。
欢迎关注
以上是关于模拟LeetCode 54. 螺旋矩阵的主要内容,如果未能解决你的问题,请参考以下文章