二分查找树

Posted 2021-03-21 基本程序猿

在开始学习二分查找树之前，首先要对树有一些了解。

在我看来，树是计算机数据机构中一种初入深水的数据。说其初，是因为树的概念本身很简单；说其入深水，是因为树并不像数组、链表之类这么基本，但是基于树却可以展开恢弘一章，由此算是能够触摸到支持日常软件乃至操作系统的一些重要基石比如数据库中的引擎等。

在接下来的一段日子里，我们就来看看树。

树是一种很形象的数据结构，它的长相就像一颗现实中的树，只不过是倒着的。所谓倒着，指的是根在上方，枝叶在下方。并且，这棵树很简单，现实中的树的枝叶可能是相互纠缠，而这棵树往往是没有回路的。

而根节点，一个比较严谨的定义，就是没有父节点的节点。并且，一棵树只会有一个根节点。

当然，上面的树仍然还是有点复杂，我们从最常见的树也是应用最多的树，开始学习树的知识。这种树就是二叉树。

所谓二叉树，显然是树的一种特例。它指的是树中任意节点最多只有两个子节点的树。形象地说，这棵树以及树的所有子树，最多开两个杈。

在具体地往下说，二叉树中又有两个特例，分别是完全二叉树和满二叉树。所谓的满二叉树，我们在堆排序中已经见过，就是所有子节点尽可能靠左的树。而满二叉树，则又是完全二叉树的特例。对于满二叉树，最下面一层排满了子节点，而完全二叉树则不一定。

空口难以理解，我们用图说话。

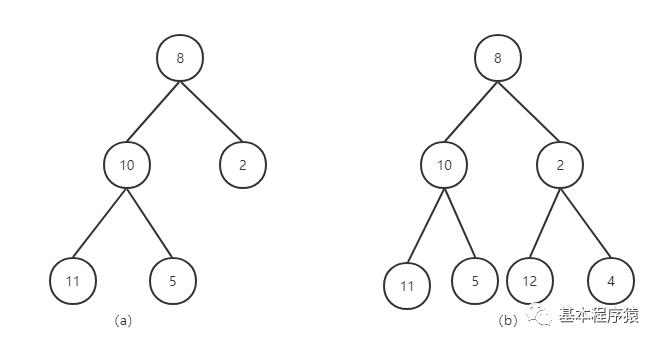
上图中，图(a)是一个完全二叉树，但不是一个满二叉树。而图(b)则是一个满二叉树，同时显然又是一个完全二叉树。二者的区别在于，在底层最多可以放4个节点，但是图(a)却只放了两个节点。

除此之外，还有一些基础知识需要我们记住。当然，也很容易理解。

1. 对于没有子节点的节点，我们将其叫做 叶子节点。
2. 树的度指的是该树中，一个父节点最多可以有几个子节点。对于二叉树，显然度就是2。
3. 树的高度指的是，一个树中的根节点到达叶子节点最多需要经过几步。

好了，现在我们就开始看正题，也就是我们所说的二分查找树。

我们目前的二分树，只是一个纯粹的度为2的树，并没有什么额外的特性。但是，等等，度为2，你有没有想到点什么？

没错，就是二分查找算法。二这个数，在计算机的世界中是有很重要的含义的，我们常说的复杂度为 ，这里的对数的底就是2。

那么，我们能不用能二分树结合二分算法来进行查找呢？如果能，我们就叫这棵树为二分查找树怎么样？

做到二分，其实关键就是当我们做抉择的时候，我们清楚地知道要么 ，要么 ，而不会说二者皆有可能。那么，我们运用在我们的树上面，我们处在一个父节点的时候，我们就应该清楚的知道要么我们要查找的元素在这个父节点的左子树上，要么就在这个父节点的右子树上（父节点本身就是我们要查找的元素除外）。

那要做到这一点，我们只需要做到，左子树的元素一定小于父子树的元素，而右子树的元素一定大于父子树的元素（反过来也行，另外这里我们不去讨论有重复元素的情况）。

当我们能够做到上面这一点时，显然我们就能够运用我们的二分法了。

思想很简单，接下来我们就来进入实战环节，看看如何构建一颗二分查找树并进行查找应用。

首先，我们先把节点定义出来。

// Node is the node
type Node struct {
    Val   int
    Left  *Node
    Right *Node
    Parent *Node
}

一个节点必要的元素有值，有左节点和右节点，同时我们也定义了父节点以方便各种操作。

下面，我们在使用二分查找树之前，首先需要知道如何构建一个二分查找树。

/*
* BST is the binary search tree.
* Its node will have parent
 */

// BST is the binary search tree, which is a wrapper of root
type BST struct {
    root *Node
}

// NewBST construct a binary search tree
func NewBST(nums []int) *BST {
    if len(nums) == 0 {
        return &BST{}
    }
    var root = &Node{
        Val: nums[0],
    }
    for i := 1; i < len(nums); i++ {
        insertBST(root, nums[i])
    }
    return &BST{
        root: root,
    }
}
// Insert insert into tree
func (tree *BST) Insert(num int) {
    var root = tree.root
    if root == nil {
        tree.root = &Node{
            Val: num,
        }
    } else {
        insertBST(tree.root, num)
    }
}
// insertBST will insert an element
// root should not be nil
func insertBST(root *Node, num int) {
    if num < root.Val {
        if root.Left == nil {
            root.Left = &Node{
                Val:    num,
                Parent: root,
            }
        } else {
            insertBST(root.Left, num)
        }
    } else {
        // right >= parent
        // In fact, left <= parent other than left < parent, we ignore this to simply this
        if root.Right == nil {
            root.Right = &Node{
                Val:    num,
                Parent: root,
            }
        } else {
            insertBST(root.Right, num)
        }
    }
}

其实，构建一颗二分查找树的关键，就是我们向一个空的二分查找树或者已有的二分查找树一个个插入新元素的过程。也就是说，这一步的核心就是上面的Insert或者说insertBST函数。

我们来看上面的函数，其实做的事很简单。

1. 首先找到根节点，如果根节点不存在，那么我们插入的元素就是根节点。这时候就可以结束了。
2. 找到了根节点。那么我们看我们应该是像左子树插入还是右子树插入。然后，根节点的左(右)子树成为了我们新的要操作的二分查找树，根节点的左(右)节点成为了新的根节点。然后继续回到1即可。这是一个递归操作的过程。

当我们有了一颗构建好的二分查找树后，还需要做的一件事就是查找。

// Search will search from the bst
func (tree *BST) Search(num int) *Node {
    return searchBST(tree.root, num)
}
func searchBST(root *Node, num int) *Node {
    if root == nil || num == root.Val {
        return root
    }
    if num < root.Val {
        return searchBST(root.Left, num)
    }
    return searchBST(root.Right, num)
}

查找仍然是一个递归的过程，上述思路的核心在于函数searchBST。

1. 我们首先看根节点是否存在（不为空）。如果不存在，那么显然也没有查找的必要了，直接返回空即可。
2. 根节点是否是我们查找的元素，如果是，那么就返回根节点。
3. 根据值的大小进行判断，判断我们要查找的元素可能在左子树还是右子树。然后，将新的左(右)子树作为我们要查找的新的二分查找树。重复1的步骤即可。

在上面的过程中，我们充分利用到了二分算法的特性，加快了我我们查找的效率。

上面的两个关键操作已经实现了二分查找树的核心功能。但是，还是有些不足，这一不足主要在于，我们的树会越来越大，因为我们不能将我们的无用元素进行删除，因此难以缩小树的规模。

所以，我们还需要实现二分查找树的最后一个操作，也就是删除操作。

// Delete delete num
func (tree *BST) Delete(num int) error {
    node := tree.Search(num)
    if node == nil {
        return errors.New("UNEXIST")
    }
    tree.delete(node)
    return nil
}
func (tree *BST) delete(node *Node) {
    if node.Left == nil && node.Right == nil { //no left and right
        if node.Parent == nil { //root
            tree.root = nil
        } else {
            if node.Val < node.Parent.Val { // node is the left of parent
                node.Parent.Left = nil
            } else {
                node.Parent.Right = nil
            }
        }
    } else if node.Left == nil || node.Right == nil { //only one branch
        var cursor = node.Left
        if cursor == nil {
            cursor = node.Right
        }
        if node.Val < node.Parent.Val {
            node.Parent.Left = cursor
        } else {
            node.Parent.Right = cursor
        }
        cursor.Parent = node.Parent
    } else { // both left
        // find min node of right branch
        var cursor = node.Right
        for cursor.Left != nil {
            cursor = cursor.Left
        }
        // then set node val
        node.Val = cursor.Val
        // recursion delete the cursor
        tree.delete(cursor)
    }
}

在进行删除之前，我们首先要确定，我们要删除的元素是否存在，这就要求我们首先进行搜索。这也是我们的Delete函数首先调用了Search的原因。如果要删除的元素不存在，那么我们也没有删除的必要了。

下面，我们就来分析，我们删除操作的关键核心函数delete。这一函数的基础是建立在我们找到了要删除的具体节点，然后尝试进行删除，并且仍然应当保持删除后我们的树仍然是一个二分查找树。

1. 如果节点是叶子节点，那么直接删除就行了。这一步是显然的，因为并不会影响到其它任何节点维持二分查找树的特性。但是，需要小心处理一下这个节点本身是根节点的情况，不过这是细枝末节的事情，不需过多讨论。
2. 如果节点本身只有左子树或者右子树。以只有左子树为例，那么如果直接用左子树的根节点代替该节点，首先显然左子树本身还是一个二分查找树不受影响。而由于左子树肯定都小于该节点，那么该节点的父节点显然也满足二分查找树的性质。这时候，删除也可以结束了。右子树同理，不需要再以布进行分析。
3. 现在到了最麻烦的地方，这个节点又有左子树又有右子树。在处理类似的问题的时候，我们往往有一个万能的策略，就是 找到一个叶子节点将这个要删除的节点替换掉。请记住这个思想，我们会在很多树里看到这个思想的应用。那么，具体找那个叶子节点呢，我们这里不妨找右子树的最小叶子节点。我们来分析一下为什么可行。假设我们将这个叶子节点放在我们要删除的节点位置，首先，这个新的节点由于并没有改变原左子树的元素，那么原左子树肯定还是一个二分查找树；而新的节点相当于将原右子树删除了一个叶子节点，那么和情况一一样，原右子树仍然是一个二分查找树。同时，新的节点由于在原来的右子树，那么一定是大于要删除的节点的，也就是说，更大于原来的左子树。与此同此。新的节点是原右子树的最左节点，也就是说一定是原有子树的最小节点，当其替换要删除的节点后，一定是小于新的右子树的。因此，这一颗新的树仍然满足二分查找树的特性。

所以，我们完成了对二分查找树的删除操作。

实现是实现完了，我们还需要进行理论上的升华，就是研究一下我们各种操作的复杂度。

对于一棵树，很重要的一个特性就是树的高度。知道了树的高度，才能进行后面的一系列操作。

那么，对于节点数目为 的二分查找树。它的树高是多少呢？

在理想情况下，我们这棵树应该长得是接近一颗完全二叉树的，所以显然高度是 。同时，这也是一个不可超越的下限。

但是，我们并不能很简单的假设我们的二分查找树是理想的。一颗二分查找树是否理想，取决于构建树的时候输入是否理想。

不妨找一个具体的例子。

假设我们的输入如下。

[2, 4, 1]

那么，根据我们刚才的分析，我们的二分查找树会如下所示。

但是，如果我们的输入不幸如下所示。

[1, 2, 4]

那么，根据我们刚才的分析，我们的二分查找树会如下所示。

换而言之，在不幸的输入下，我们的树的高度可能是 的。比如我们的输入一直是递增的顺序，那么就会永远只有右子树。

所以，我们的二分查找树的高度会是 和 之间。好在，如果我们的输入是随机的，那么我们的左右子树会个数差不多，那么就会接近 。反之，就会比较接近 。

那么，基于树的高度为 的前提，我们的各项操作复杂度是多少呢？

首先，是我们插入元素。当我们插入元素时，这个新的元素一定会成为叶子节点。那么，我们最多需要遍历的次数就是树的高度，因此复杂度为 。

接下来，是我们查找元素。当我们查找元素时，我们最多会找到叶子节点。那么，我们最多需要遍历的次数同样就是树的高度，因此复杂度为 。

最后，是我们删除元素。在删除之前，我们首先需要进行查找，因此有一个复杂度为 。下面，我们就来看实际删除的复杂度。

1. 在我们删除的情形1中，直接删除就行了，因此复杂度为 。
2. 在我们删除的情形2中，需要修改一些指针，但是并不需要再进行递归或者循环，因此复杂度同样为 。
3. 在我们删除的情形3中，除了需要修改一些指针，还需要修改元素的值，但是同样并不需要再进行递归或者循环，因此复杂度同样为 。

所以，总的来说，删除元素的复杂度仍然为 。

因此，我们也不难意识到，对于二分查找树，其操作的复杂度严重依赖于树的高度。但是，遗憾的是，简单的二分查找树的简单特性无法维护稳定的树的高度。因此，我们需要想办法控制一个二分查找树的高度稳定在 的复杂度，这显然需要加上更多的限制。而这不同的限制，也就使得我们构造了不同的新树。这些新的树，就是我们接下来的文章要描述的。