Pytorch神器
Posted 奇点
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Pytorch神器相关的知识,希望对你有一定的参考价值。
上次我们的连载讲到用最简便的方法,也就是pip方法安装Pytorch。大家都成功了吧。
那我们从今天开始,就一步一步把Pytorch的项目工程落实一下。
老实说,Pytorch的学习牵扯到了非常多的学术和工程技术方面的问题,比如最优化问题、Python语法问题,Numpy包学习问题等等。这些问题如果从零开始一步一步都学过来的话,是非常花费时间的。在这里,为了让大家不要产生太大的恐惧感,我准备使用最“简便”的方式来给大家做讲解——也就是使用囫囵吞枣的方式来做讲解。相信我,入门速度杠杠的,简便易懂,至于深挖细挖就留在以后再做相关领域的时候再仔细研究就好了。不过只请各位确认一件事,就是至少你要有一门语言(不论是C、C++、Java、Pascal等)任何一门还是要熟练掌握,这样做起来知识迁移也方便。好,现在闲言少叙,书归正文。
我们的连载目标非常明确,就是把Pytorch官方给的Tutorial(辅导材料)的内容给理解透彻,下面的新工作就好办了,因为它们无非是这些概念的重组或者变形。
它的git项目代码位置在:https://github.com/yunjey/pytorch-tutorial
1、请安装git:
使用命令:sudo apt-get install git
2、请下载这个git项目的代码
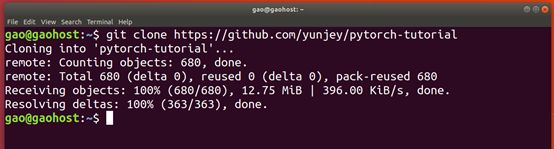
输入命令:git clone https://github.com/yunjey/pytorch-tutorial
下载完后使用命令查看:ls -la
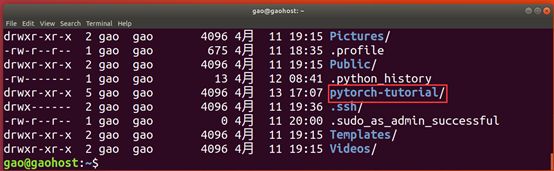
这个pytorch-tutorial就是下载下来的项目代码文件夹了。
3、进入文件夹
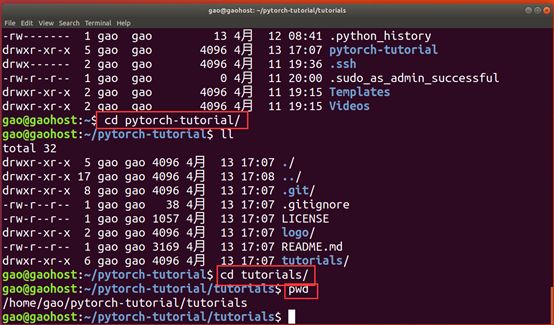
进入pytorch-tutorial路径:cd pytorch-tutorial
进入tutorials路径:cd tutorials
查看当前路径:pwd
在这个例子中,我的路径是/home/gao/pytorch-tutorial/tutorials,大家在做实验的时候请根据自己的路径来实际操作就可以了。
4、查看文件夹内容
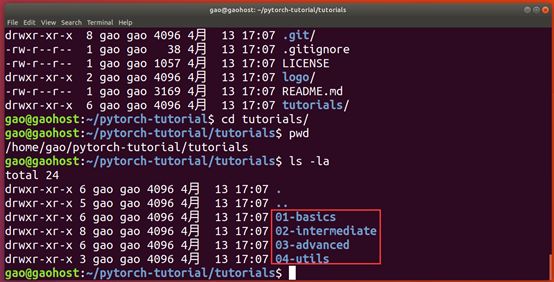
使用ls –la命令可以看到,在这个文件夹中有四个文件夹分别是:
01-basics
02-intermediate
03-advanced
04-utils
从字面意思看,它分别代表初级案例、中级案例、高级案例、应用案例,那么我们就从最基础的初级案例01-basics来入手吧。
5、原理解释
进入01-basics:cd 01-bascis
展示文件夹内容:ls –la
这里有4个文件夹,今天我们先找最简单的线性回归linear_regression入手好了。
进入文件夹linear_regression:cd linear_regression
展示文件内容:ls –la
这里只有一个文件,就是main.py
我们查看一下main.py的内容是什么,不过在此之前我们需要安装一下vim(一个古老的Linux下的文本编辑器)。
使用命令安装vim:sudo apt-get install vim
为了阅读方便,我们需要让vim能够显示行号。
使用命令:sudo vim /etc/vim/vimrc
在尾部加入set nu
保存文件。
如果你觉得vim用起来不喜欢,也可以考虑使用任何的文本编辑工具,或者Pycharm等专业的Python编辑器。
使用命令vim main.py打开文件,可以看到文件并不长,只有60多行。
先划一下每个部分的大致功能:
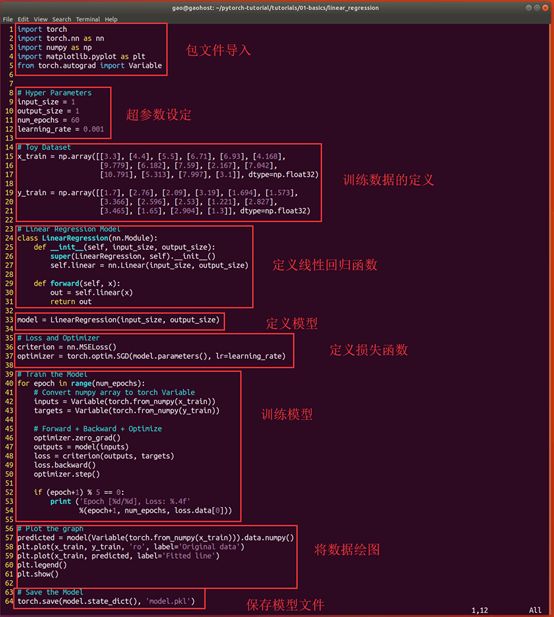
虽然只有60行,但是没有基础的读者很难理解它们究竟在说什么。那我们从线性回归开始说起,我争取用最短的语言让大家明白线性回归的内容。
(1) 监督学习(Supervised Learning)
首先,在机器学习领域里,有一个范畴叫做“监督学习”,所谓监督学习我们可以粗略理解成为这样一个事情。如果我有一个函数
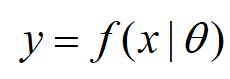
其中x就是平时说的自变量x,y就是输出的函数值,theta就是待定系数。我们来看一个例子:y=2x+3,那么当我给定x=1的时候,y=5,在这个公式中theta就是2和3。在这个过程中,只要给一个确定的theta,给定一个x来求y是非常简单的,就是小学的加减乘除。
不过,在机器学习中,这个过程是反过来的——能不能在知道一堆x和他们对应的y的前提下,来推导出theta是什么。如果这个过程可以实现的话,那么接下来一旦知道theta,就可以通过输入一个x来确定输出的y了。这个过程就需要机器进行学习了,从x和y中学习到他们具体的映射关系——也就是theta。这个过程就叫做训练(Training)。在明确如何训练之前,我们可以想象,如果这种通过输入一个x,和一个y,就能让机器人学到theta,然后完成整个映射逻辑学习的话。那么如果能够把一个高智能机器人的输入的一切环境描述成一个x,把应该做的输出描述出一个y,那么就从理论上完全有可能把机器人训练成一个高级智能机器人,至少理论上是可以的。至少人脸识别这样的应用是这种形式——输入一个图片,输出一个人脸位置;至少图片分类也是这样的——输入一个图片,输出这个图片的分类内容,是猫还是狗。这里的x和y等于都是事先知道的,这种自变量x和输出函数值(标签值)都已知的机器学习叫做监督学习。那么线性回归可以吗?就是这种用
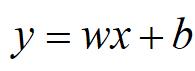
的结构描述的最简单的x和y的映射关系的模型可以吗?当然没问题。
(2) 线性回归
这里说的w和b就是刚刚说的theta,就是待定系数,就是我们要从训练中得到的值。这里的b就是一个实数,而w和x就可能是多维向量了,或者1维或者n维。
1维很好理解,w*x就是两个数字相乘。
n维的情况下,y=wx+b这个的含义就是指空间向量相乘(也就是矩阵乘积的特殊形式),看个具体的例子你就能明白。
例如:
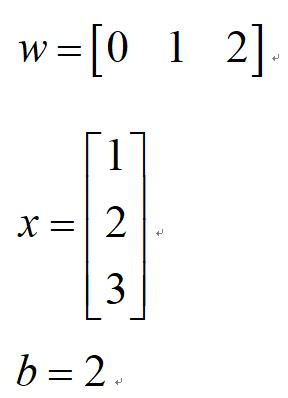
那么此时y等于几呢?
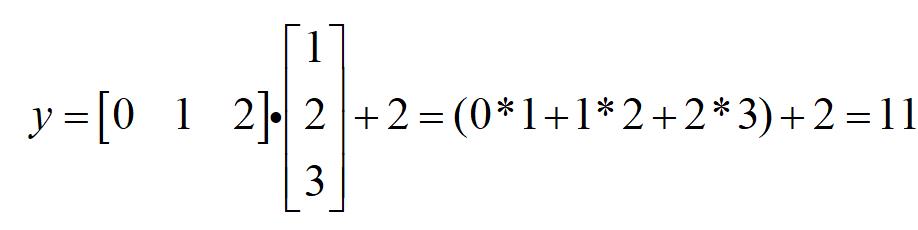
wx实际就指的是一个1行n列,和一个n行1列的向量相乘,即对应维度的值相乘(这个例子中n=3),就这么简单。
如果w和x都是一维的,那就是普通的实数乘法了,很好理解。现在的问题是x和y都知道了,怎么得到w和b呢?
(3) 梯度下降法(Gradient Decent)
有一种方法叫做梯度下降法,过程大概是这样:
我们给定一个w和一个b,这样只要给我一个x,我就一定能得出一个y来。问题是,这个y可能跟客观上应该输出的那个y偏差很大,因为w和b是“瞎给”的。那么这个误差究竟有多大呢?我们写出来看看
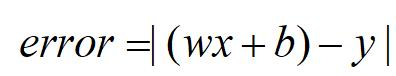
也就是刚刚说过的这几个值进行计算相减,很容易的出来。这里加了一个绝对值,言外之意就是不管相减是正还是负,只要不是0,那就都是误差,误差是一个大于等于0的数字。
在这个学习的过程中,我们不能使用一个x和它对应的y来做样本,因为这样会有一个问题,那就是过一个点会有无数多种的w和b的解能够满足y=wx+b的这个解析式。这种问题叫做过拟合(Overfitting),以后我们会讨论。总之,如果我们想求一个y=wx+b的待定系数w,b就不能只给一个点,这样没有意义,会得出无数种解来。
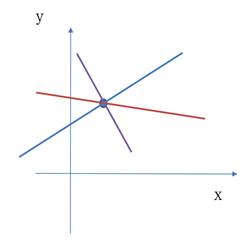
而我们实际的情况和实际的期望大概是这样:
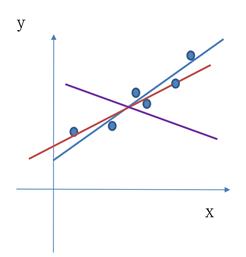
如图中所示,三条线各自有各自的w和b。其中蓝线和红线所示,基本都穿过了给定的x,y样本点,而紫色的那条线看着就不太合适,因为看上去误差就很大。蓝色和红色起码看着还靠谱一些,那么哪条更好呢?别急,这个问题我们让这两条线比一个数字就可以知道谁更好了,比Loss。
所谓Loss也叫损失函数,是用来描述模型的拟合值和标准值之间误差的一个函数。所谓拟合值,就是指自变量x通过f(x)表达式计算得到的值,而这个x所对应的y就是标准值(或者称为标签值),它们的差值刚刚我们已经见过一次了,而现在我们要写一个更为标准一些的形式:
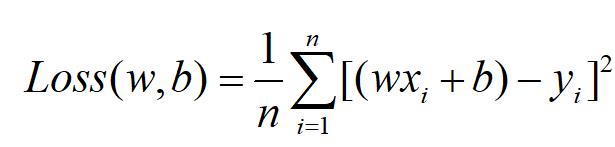
这个希腊字母读作sigma,表示连续加,或者你可以理解成一个循环,从1到n的循环。循环的内容就是把给定的n个x和n个y逐个进行(wx+b)-y的这样一个计算,其中i你就可以理解成为循环变量,就好像for i in range(n)这种格式。平方是为了消除负的差值,前面的1/n指的是平均在一个样本上的损失大小。
因为这n个x和n个y是已知的数值,也就是训练的样本,所以Loss(w,b)这个函数中,其实未知数不是x和y,而是w和b才对。
注意,现在的问题转化了,这个Loss(w,b)既然说是指在w,b确定的情况下,平均在一个样本上的误差,那么w,b取什么合适其实就相当于取什么值能满足误差最小,越小越好。能求出来吗?能,必须能!
这个损失函数,我们把它展开其实可以得到这样一个形式:
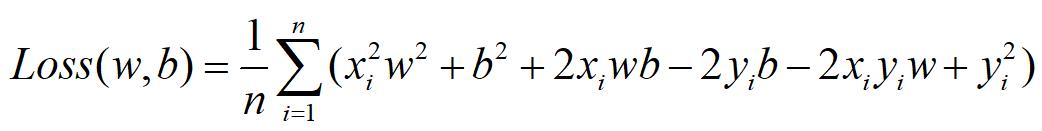
其中的xi和yi都是已知数,那么就是一个w二次项,b二次项,wb乘积二次项,w一次项,b一次项,常数项的一个完整的二元二次方程。在空间里大概长这样子,是一个碗:
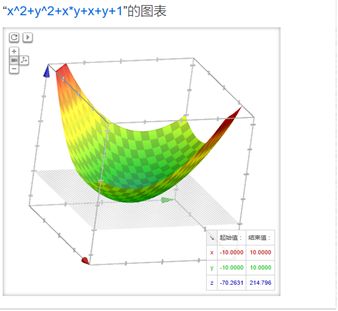
这是一个w,b,Loss三维空间上的函数图像,碗表面上的每一个点都是一个(w,b,Loss)的值,很直观,“碗底”的位置就是Loss最低的值,现在要求的是这个点上w和b取什么值。
这种方程一般是很难解出来的,所以通常用另一种办法,梯度下降法——主角终于出场了。过程如下:
首先初始化一个w0和b0点,此时Loss(w0,b0)一定会有一个值,它就在碗表面某一个位置。现在我希望它朝着碗底的方向运动。那么使用以下公式:
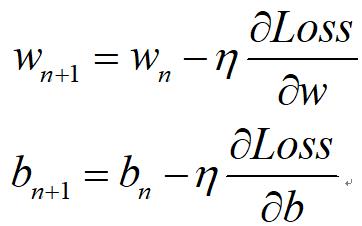
这俩公式虽然长得吓人,但是内容意义很简单。
解释:
wn+1指的是第n+1次和第n次迭代的关系;这个希腊字母eta表示学习率,是一个很小的数值,比如0.01,0.05或者更小的值;最后是Loss对w求偏导数,含义就是这个碗边缘沿着w轴的斜率,毫无疑问,这个斜率一定是在碗底的部分最小,为0,切线几乎是“平”的;而越远离碗底的部分越立陡,斜率绝对值越大。Loss对b求偏导数那一项同理。这样一来,这两个表达式解释成代码大概是这感觉:
eta =0.01
delta =0.01
for i inrange(n):
w=w-eta*(((w+delta)*x+b)-(w*x+b))/delta
b=b-eta*((wx+b+delta)-(wx+b))/delta
这里的eta,就是学习率,在例子中给的0.01,这样一个值是希望更新的时候步子能够迈得小一些,如果过大的话,很可能一步就迈过的碗底。
这里的delta给的0.01,从后面这个部分来看,其实就是为了求斜率而已。这也算一个小技巧吧,毕竟直接求一个函数导数的表达式,再通过表达式求斜率很复杂。然后我们并不需要这样,只需要把它的斜率值求出来就行了,按照定义就是这个公式:
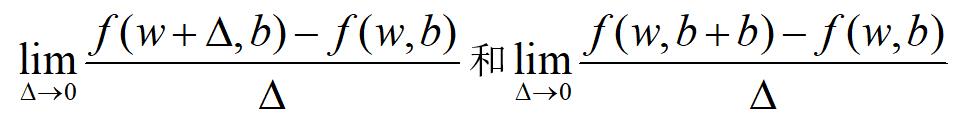
也就是梯度,只是这里的delta我们在例子中只是示意性的取了0.01而已。这样我们就可以通过不用求函数导数表达式,再求导函数值的方式来求解了。
这个更新的公式(这段代码)可以保证w和b沿着梯度下降的方向去更新,所以叫做梯度下降法。在陡峭的边缘,由于斜率大,梯度大,更新的速度快;在碗底附近,斜率小,梯度小,更新的速度慢。它能保证w和b稳稳当当地更新到碗底附近。这么复杂的公式需要我们去写吗?还真不用,Pytorch都给我们集成了。
好了,到这里我们的铺垫工作算彻底完成了,总结一下。
1、 我们需要拿到n个x和它们对应的n个y,也就是n个(x,y)的样本;
2、 假设一个待定的w和一个待定的b;
3、 定义好损失函数Loss
4、 对损失函数做梯度下降
这样就能求出
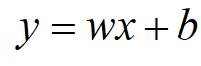
里面的w和b了。然后再给我任意一个x,我都能求出对应的y。完美。
好现在,我们再回过头来看代码。
5、 代码解释

1~5行:包文件导入,没啥好解释的,每种语言都有这种东西。不赘述了。
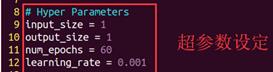
9~12行:超参数定义。所谓超参数就是那些在训练中无法通过训练得到的,这与我们刚才说的w和b完全不同(这两个是能通过训练学到的)。超参数通常只能在训练开始之前人为手工设定。
input_size是指输入向量的大小,在这里定义为1,就是x是一个1维变量的意思。
output_size是指输出向量的大小,也是一个1维变量,就是y。
其实这两句是在变相定义w还有y的维度。
num_epochs在这里指的是循环次数。所谓epoch,指的是这样一个概念。每一个训练样本都带入训练执行一次叫做一个epoch。
learning_rate就是我们前面说的eta,学习率。

15~21行:训练数据的定义。在这里我们可以看到x_train就是说的x变量,定义成了一个15个元素的数组(其实是矩阵,我们暂时先这样理解),y_train也一样。当然在实际项目应用的过程中,数据的来源不会是这样,而是应该从文件中读取。
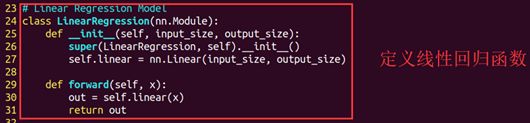
24~31行:定义了一个线性回归类LinearRegression,就是线性回归的意思。这个类中的第27行,这个类的linear被定义成了torch.nn.linear。也就是说,可以用linear来代替torch.nn.linear的写法,仅此而已,算做了一个简化吧。在这里,相当于定义了模型函数为y=wx+b,并且w是1维,b也是1维。
29行:forward就是做个正向转播,看表达式就是一个给定x,用linear求y的过程。

33行:做了一个封装,声明了一个model变量,LinearRegression的实例化。
36行:criterion的英文含义是“标准”,从表达式上来看,是定义了损失函数的类型。后面写的是nn.MSELoss。也就是说,criterion用的是MSELoss,就是Mean Squared Error——平均平方误差,也就是
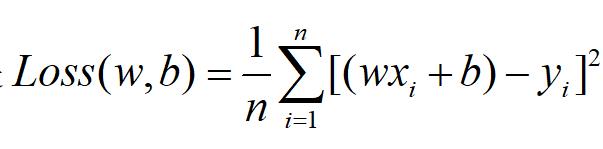
37行:定义optimizer为torch.optim.SGD优化器,也就是随机梯度下降StochasticGradient Descent算法。这里只提一句就好,随机梯度下降和我们前面说的梯度下降在本质上没有太大的区别。只不过,梯度下降是所有的样本都参与了计算梯度每次迭代更新w和b。而随机梯度下降是每次从所有的样本中随机挑选一部分来计算梯度。这种原理是源于统计学中的抽样(Sampling),因为抽样就是从一大堆样本中找出一部分来做代表,根据这些代表来做统计。这样一来,产生了一个优点和一个缺点。
优点是:每次计算量会变小,每次更新运算的速度会加快,内存的占用也会相应减小。
缺点是:由于每次都是抽样计算,所以在统计学抽样上体现出来的缺点就会很很明显。每次计算中梯度都会不太相同(因为抽样的缘故)。会导致收敛的方向不确定,更新的次数有可能会增多。
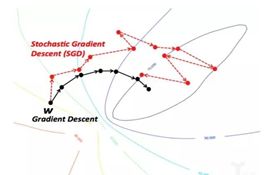
model.parameters()就是指被优化的对象,就是指w和b。
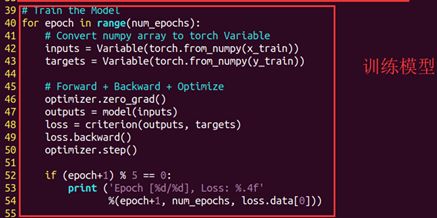
40~54行:循环,做60次。做一个格式转换,x叫做inputs,y叫做targets,都变成Pytorch的变量类型。
46行:梯度归零。
47行:把x输入模型f(x),产生一组拟合值,也就是每个x对应的y都求出一个y=f(x)的值。当然这个时候就是w和b不靠谱的时候,输出的y误差会很大。
48行:损失函数Loss的值就是求标签值targets和拟合值y的差,再平方,再除以n(也就是除以15)。
49行:Loss做一个反向传播,所谓的反向传播就会求出w和b的梯度。
50行:optimizer做一个单步更新,此时w和b都朝着碗底近了一步。
52~54行:每5次更新(5个step)打印一次Loss的大小。
就这样循环60次。其实这个次数也可以是别的次数,设置的次数只要能够保证最后的误差值足够小就可以了,因为越执行肯定w,b的位置越贴近碗底,梯度越低,更新速度越慢。
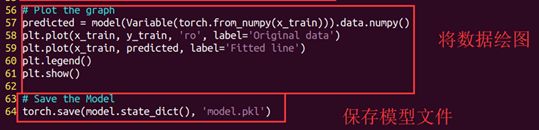
57~61行:把训练样本x带入训练好的模型,然后做出一组y来,只不过这个地方的y叫predicted。
然后把x和y的点画图画出来。
64行:最后保存训练好的模型文件。
在执行这个文件之前请先安装matplotlib
输入命令:pip3 install matplotilb
然后再安装python3-tk
输入命令:sudo apt-get install python3-tk
执行文件:python main.py
这样就可以看到结果了。
由于待定系数少,所以即便是用CPU都是秒得。
怎么样简单吧,这就是我们用Pytorch来构建的第一个最简单的机器学习模型,线性回归。
如果你对线性回归和梯度下降的过程还是觉得不够详细的话,请参考本身的另一本著作《白话深度学习与Tensorflow》,里面的解释更为详细一些。
以上是关于Pytorch神器的主要内容,如果未能解决你的问题,请参考以下文章