数据挖掘十大算法 The k-means algorithm

Posted 2021-05-02 林海数原

点击标题下「林海数原」可快速关注

算法综述：

k-means algorithm算法是一个聚类算法，把n的对象根据他们的属性分为k个分割，k < n。它与处理混合正态分布的最大期望算法很相似，因为他们都试图找到数据中自然聚类的中心。它假设对象属性来自于空间向量，并且目标是使各个群组内部的均 方误差总和最小。

　　

假设有k个群组Si, i=1,2,...,k。μi是群组Si内所有元素xj的重心，或叫中心点。
　　

k平均聚类发明于1956年， 该算法最常见的形式是采用被称为劳埃德算法(Lloyd algorithm)的迭代式改进探索法。劳埃德算法首先把输入点分成k个初始化分组，可以是随机的或者使用一些启发式数据。然后计算每组的中心点，根据 中心点的位置把对象分到离它最近的中心，重新确定分组。继续重复不断地计算中心并重新分组，直到收敛，即对象不再改变分组（中心点位置不再改变）。
　　

劳埃德算法和k平均通常是紧密联系的，但是在实际应用中，劳埃德算法是解决k平均问题的启发式法则，对于某些起始点和重心的组合，劳埃德算法可能实际上收敛于错误的结果。（上面函数中存在的不同的最优解）
　　

虽然存在变异，但是劳埃德算法仍旧保持流行，因为它在实际中收敛非常快。实际上，观察发现迭代次数远远少于点的数量。然而最近，David Arthur和Sergei Vassilvitskii提出存在特定的点集使得k平均算法花费超多项式时间达到收敛。
　　

近似的k平均算法已经被设计用于原始数据子集的计算。
　　

从算法的表现上来说，它并不保证一定得到全局最优解，最终解的质量很大程度上取决于初始化的分组。由于该算法的速度很快，因此常用的一种方法是多次运行k平均算法，选择最优解。
　　

k平均算法的一个缺点是，分组的数目k是一个输入参数，不合适的k可能返回较差的结果。另外，算法还假设均方误差是计算群组分散度的最佳参数。

算法原理：

聚类算法用于根据数据的特征发现数据项的相似性，并将相似的数据项放在同一个组中，相似性采用距离进行描述。

K-means聚类

简单的说，一般流程如下：先随机选取k个点，将每个点分配给它们，得到最初的k个分类；在每个分类中计算均值，将点重新分配，划归到最近的中心点；重复上述步骤直到点的划归不再改变。下图是K-means方法的示意。

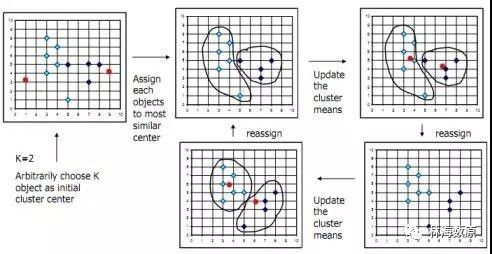
K-Means算法的SAS实现

K-means算法可以用SAS的proc fastclus实现。主要涉及两个问题。

首先是初始点的选择。如果指定replace=random，则系统随机选取maxcluster选项指定个数的完整观测作为凝聚点。如果分析员对研究情景比较了解，可以利用专业知识指定初始分类，那么可以在proc fastclus中设定seed=dataset选项，SAS会从dataset中读取前k个观测作为初始凝聚点。此外，SAS还提供了系统自动选择初始凝聚点的方法，该方法需要指定maxclusters和radius选项，其中radius为凝聚点之间允许的最小距离。默认值是maxclusters=100，radius=0，效果是选取数据集中的前100个观测作为凝聚点。fastclus过程总是选择第一个完整观测作为第一个凝聚点，然后依次考察剩余观测，与第一个凝聚点的距离大于radius指定值的观测作为第二个凝聚点。当凝聚点的个数未达到maxcluster，且所考察观测与已有凝聚点间距离均大于radius指定值时，则所考察的观测成为下一个凝聚点。如果一个观测完整且与所有凝聚点距离均大于radius，但凝聚点个数已经达到最大值，此时fastclus过程进行两种替换检验，检验能否用当前观测替换已有凝聚点。第一个检验是替换距离最近两凝聚点检验，如果凝聚点与当前观测的最小距离大于已有凝聚点的最小距离，则一个已有凝聚点将被替换，当前观测将替换距离最近的两个凝聚点中的一个，使得替换后当前观测与最近距离两凝聚点中未被替换的那个距离最远。第二个检验是替换当前观测最近凝聚点检验，如果当前观测到除最近凝聚点外的所有凝聚点的最小距离大于当前观测最近凝聚点到所有其他凝聚点的最小距离，进行替换。如果两种检验都说明该观测不能替换已有凝聚点，则转向下一个观测，直到考察完数据集中的所有观测。当然，这种检测可以用replace=none|part|full来控制，none表示不进行替换检验，part表示只进行第一种替换检验；full为默认值，两种替换检验都进行。

另一个问题是分类的修改方法。默认的方法是按批修改法，即选定一批凝聚点后；将所有观测按与其距离最近的凝聚点归类；计算每一类重心，将重心作为新的凝聚点，若新凝聚点与旧凝聚点完全重合，则终止算法，否则重新归类。批量修改法是全部观测调整完毕后，才改变类的凝聚点，而逐个修改法是每个观测一旦调整后立即改变类凝聚点，而立即改变需要算法即时验证改变后的凝聚点集合是否仍然满足radius的约束。如果不满足radius的约束，SAS会将小于radius的两类合并，计算重心，作为合并后类的凝聚点，如此往复，直到凝聚点满足radius条件。要让SAS执行逐个修改法，需要声明drift选项。

补充

K-means聚类算法的问题是，均值的计算受异常点的干扰比较严重。为了克服这个问题，可以采用K中值法。

K-medoid聚类

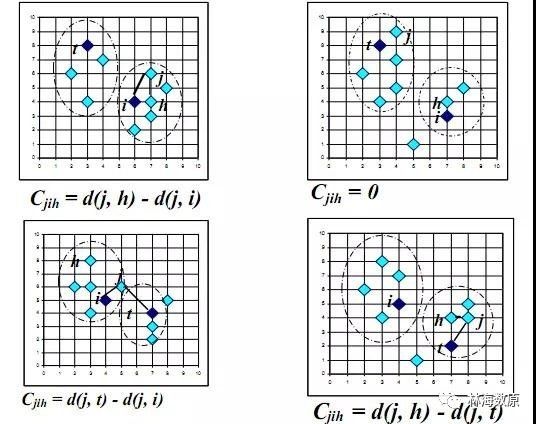
PAM（Partition Around Medoids）是K-medoid的基础算法，基本流程如下：首先随机选择k个对象作为中心，把每个对象分配给离它最近的中心。然后随机地选择一个非中心对象替换中心对象，计算分配后的距离改进量。聚类的过程就是不断迭代，进行中心对象和非中心对象的反复替换过程，直到目标函数不再有改进为止。非中心点和中心点替换的具体类别如下图分析（用h替换i相对j的开销）。

PAM算法的问题在于伸缩性不好，需要测试所有的替换，只适用于小数据量的聚类。

为了提高该算法的可伸缩性，有人提出了CLARAN算法，本质如下：从总体数据中生成多个样本数据，在每个样本数据上应用PAM算法得到一组K中值点；取出所有样本中结果最好的那一组作为最后的解。CLARAN算法存在的问题是，算法的聚类质量依赖于样本的质量。

为了提高PAM和CLARAN算法的聚类质量，有人在CLARAN算法的基础上提出了CLARANS算法。与CLARAN相比，最大的区别在于没有一个时刻算法局限于固定的一个样本中，自始自终，算法的样本数据都是随机抽样的。其算法过程如下。将每套k个中值点作为一个节点，若两个节点之间有k-1个点相同，则成为邻居。用户事先指定两个数，一是最大的邻居数，二是最大的局部最优点数。算法随机选取一个当前点，随机地取出其中的一个邻居，看目标值是否有改进，如果有改进，则用邻居替代当前点，重新开始搜索邻居的过程；若抽取了最大邻居数的邻居，发现当前点最优，那么就找到了一个局部最优点。找到一个局部最优点后，再随机抽取一个当前点，进行上面的过程，直到找到了用户指定最大数量的局部最优点。比较每个局部最优点的目标值，取最优的那个点作为结果，即可得到k个中值点，于是k个类就可以轻松得到。CLARANS算法的效果不错，但算法复杂度更高。

释放数据价值，提升生活品质

www.thdata01.cn