算法实战---OC快速排序

Posted 2021-05-02 IT实战联盟

** 近来在巩固数据结构和算法的知识, 动动手操作操作. **

能讲出来是真的懂了, 分享是件快乐的事

第一. 先来一张算法的时间复杂度/空间复杂度以及使用场景

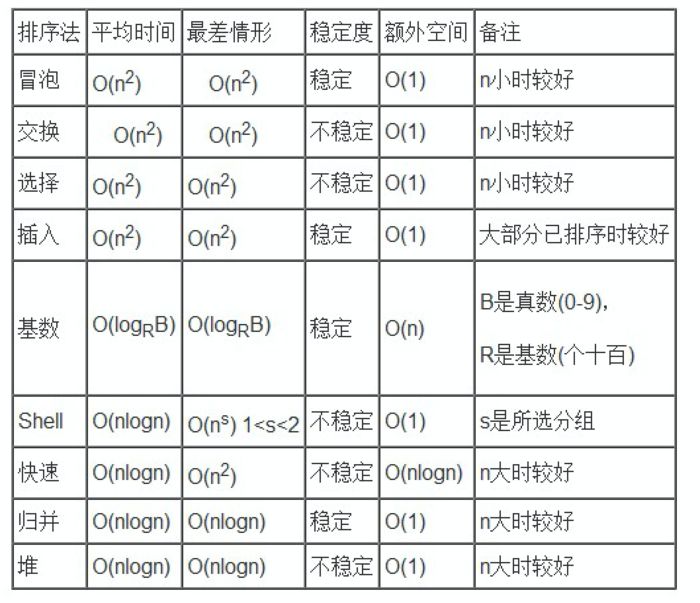
网上下载的图片

网上有一个排序算法的动画演示，非常有趣。大家可以参考一下;

第二. 那些专有名词的计算方法

时间复杂度定义

在进行算法分析时, 语句总的执行次数T(n)是关于问题规模n的函数, 进而分析 T(n) 随 n 的数量级.
记作: T(n) = O(f(n)), 表示随问题规模 n 的增大, 算法执行时间的增长率和 f(n) 的增长率相同, 成为算法的渐进时间复杂度

计算方法

1. 用<常数 1 >取代运行时间中的所有<加法常数>;
2. 在修改后的运行次数函数中只保留<最高阶项>;
3. 如果最高阶项存在且不是 1, 则取出与这个项相乘的常数.

如: 计算函数的时间

for (int i = 0, i < n, i++){    for (int j = i, j < n, j++){        //时间复杂度为 O(1)的方法
    }
}

等于多少呢? 答案是 O(n²), 觉得函数中的第二个for 循环不是 < n, 对吧?

按照上面的规则:

总的执行次数: 

n + (n - 1) + (n - 2) + .... + 1 = n(n + 1) / 2 = n²/2 + n/2上边的求解方法:1. 没有加法常数不予考虑 ===> n²/2 + n/2;2. 只保留最高阶 ===> n²/2;3. 去掉这个项目相乘的常数(1/2) ===> n²;4. 最终为O(n²);

总的时间复杂度为: n * n => O(n²)

明白了吧

第三. 本文的主题: 快速排序

快速排序是 C.R.A.Hoare 于 1962 年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

分治法的基本思想

1. 将原问题分解为若干个规模更小但结构与原问题相似的子问题;
2. 递归地解这些子问题，然后将这些子问题的解组合为原问题的解。

快速排序的整体思想

1. 每次一个基准点<pivot>，
2. 将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。
3. 重复1 2.

快速排序的动画演示:

1170656-aa523ec3ba9a2909.gif

参考<啊哈算法>这本书, 整理自己的理解;

1.待排序数组

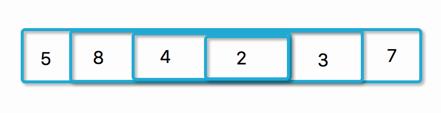
待排序

2. 左右开工

Paste_Image.png

从右向左, 从左向右依次执行, 如下图所示

Paste_Image.png

用标准的OC代码来实现一下

- (void)quickSortWithArray:(NSMutableArray *)array left:(NSInteger)left right:(NSInteger)right{    //数组不需要排序
    if (left >= right) return;    
    //数组第一个位置
    NSInteger i = left;    //数组最后一个位置
    NSInteger j = right;    //将第一个位置的<value>作为---基准
    NSInteger pivot = [array[left] integerValue];    
    while (i != j) {        //从后往前走, 直到找到 大于 <基准> 的数字, 此时 j 保存那个数字的下标位置
        while (i < j && pivot <= [array[j] integerValue]) {
            j--;
        }        //再从前往后走, 直到找到 小于 <基准> 的数字, 此时 i 保存那个数字的下标位置
        while (i < j && pivot >= [array[i] integerValue]) {
            i++;
        }        //互换位置
        if (i < j) {
            [array exchangeObjectAtIndex:i withObjectAtIndex:j];
        }
        
    }    //最终将基准数归位, 因为i == j, 需要将<基数所在位置的value>与<i/j相等的位置的value>互换位置
    [array exchangeObjectAtIndex:i withObjectAtIndex:left];    //继续左边的排序
    [self quickSortWithArray:array withLeft:left andRight:i - 1];    //继续右边的排序
    [self quickSortWithArray:array withLeft:i + 1 andRight:right];
}

**Demo也有的, 请看Github, Demo都会加上不少的注释滴 **

多动手, 多思考, 多写多画,
可能每种语言都有类似的API, OC中有 exchangeObjectAtIndex .. withObjectAtIndex 的 -_-

更多精彩内容请关注“IT实战联盟”哦~~~