快速排序的套路
Posted 广州小程
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了快速排序的套路相关的知识,希望对你有一定的参考价值。
之前小程介绍合并排序的套路时,提到了“重用”与“分治”的套路,这两个套路,在快速排序的算法设计上,同样有所体现。
在“重用”套路上,快排跟合排一样,都是重用自身(因为自身就具有排序功能),让某段数列变得有序。
在“分治”套路上,相比于合排,快排更具有心思,不是简单的“分”,而是有设计的巧妙的“分”,这也使得在重用自己变得有序之后,不需要再跟其它段的数列进行合并。
本文介绍快速排序的算法套路,也就是重用与分治的套路。
重用
分治
快速排序的算法设计,经典套路在于“分治”套路,它的“分”跟合排不一样。
合排的“分治”很简单,都是对半地一分为二,分出来的两段数列,在重用自己变得有序之后,还需要合并起来,因为这两段数列没有绝对地哪段更大,需要比较着来合并。
而快排的“分治”套路,是精心设计的,并不是简单的对半一分为二,而是先在数列中找出一个位置,这个位置上的值,均大于它左边的数列的值,均小于它右边的数列的值,也就是出现“左小右大”的排列。那么,这个位置(以及值)就是最终排序后的位置,是不需要再动的,因为这个位置的左边的数列都小于这个位置的值,而右边的数列都大小这个位置的值。于是,可以很自然地,分出“左小”的数列,以及“右大”的数列,对于这两个数列,再次重用自己就可以变得有序,而且,有序后的两个数列并不需要再次合并,因为左数列总是小于右数列。
所以,快速排序所体现的套路,最经典的就是分治套路,而且是精心设计的分治。
以上,主要讲解了快排的分治与重用的套路,接下来介绍快排更具体的设计思路。
在设计分治的时候,需要找到一个位置,使得“左小右大”,这一个操作,可以视为一个标准作业,叫作“确定中位”,显然这个操作也是会不断地被重用到的。
小程介绍一下如何确定中位,这个标准作业也是设计快排算法的关键点。
确定中位前,先要确定中位值。
中位值,坐在中位,左边的数比中位值小,右边的数比中位值大。于是,这个中位值就是最终排序后的一个元素,它的位置不需要再调整。然后,就中位两边的两部分,再重复调用自身来排序(实际也是定值定位的操作),即可解决问题。
(一)定中位值
这个很随意。
一般,可以选择数列最左边,或最右边的值作为中位值。
也可随机地选择一个值(包括中间的值),然后跟最左或最右的值进行互换,于是又回到了一般的思路。
对于中位值,需要记录下来,因为数列中的中位值很快就会被其它值覆盖。
中位值,最终要坐到中位。
(二)定中位
定中位,是实现快排的最复杂的流程。
确定出来的中位,用来放置中位值。
最终,要保证“左小右大”,即中位左边的数小于(或等于)中位值,而右边的数大于(或等于)中位值。
小程这里介绍两个设计思路。
(1)“左小右大”
参考网上的一个图,最终ij相逢的位置,就是中位: 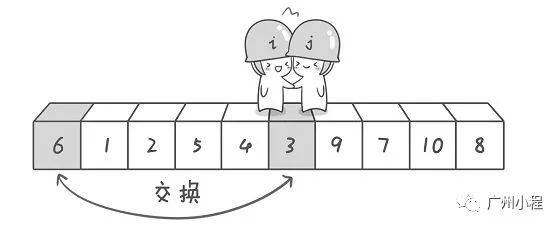
设计两个索引i跟j,分列数列的两端。不断地把小值扔到i的位置,然后把大值扔到j的位置,一直保证[start,i]是小值,[j,end]是大值。
最终,i==j,设置好中位值,再返回i。
在拿到中位后,数列分为[start,i-1]跟[i+1,end]两部分,用次用“快排”的算法解决它们。
这是“左小右大”的一个演示图: 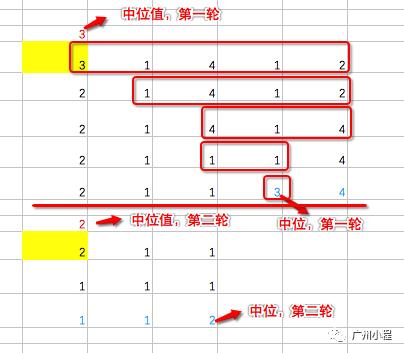
可以看到,每一轮的定位,都是不断地把红框区域变小,最终就是中位。
另外,有一个细节,当arr[j]覆盖到左边后,就相当arr[j]是一个空出来的位置,等着arr[i]来覆盖,所以,这时一定是i++,再拿arr[i]跟中位值比较。在arr[i]覆盖到右边后,也是同样的道理,一定是j--,再拿arr[j]跟中位值比较。
根据这种设计思想,可以这样编码实现(小程再次强调,算法套路跟编码是两个话题):
#include <stdio.h>
int position(int* arr, int i, int j) {
int v = arr[i];
while (i < j) {
while (i < j && arr[j] >= v) {
j--;
}
if (i<j) {
arr[i++] = arr[j];
}
while (i<j && arr[i]<v) {
i++;
}
if (i<j) {
arr[j--]=arr[i];
}
}
arr[i]=v;
return i;
}
void _quicksort(int* arr, int i, int j) {
if (i<j) {
int pos = position(arr, i, j);
_quicksort(arr, i, pos-1);
_quicksort(arr, pos+1, j);
}
}
void quicksort(int* arr, int size) {
_quicksort(arr, 0, size-1);
}
int main(int argc, char *argv[])
{
int arr[] = {4, 2, 5, 1, 6, 6, 8, 9, 8, 3};
int size=sizeof arr/sizeof *arr;
for (int i = 0; i < size; i ++) {
printf("%d, ", arr[i]);
}
quicksort(arr, size);
printf("\nafter_sort:\n");
for (int i = 0; i < size; i ++) {
printf("%d, ", arr[i]);
}
printf("\n");
return 0;
}
(2)“左小”
把所有小值扔到左边,最后,中位就是小值堆的右边的第一个位置。
可以取list[end]即最右的数值为中位值(或最左边也可以)。
设计i、j索引。保证[start,i]为小值,而j用来遍历所有数值(从start到end),如果发现list[j]小于中位值,则扩大[start,i]并把小值扔到里面(list[j]与list[i]互换即可)。
最终,i+1为中位。
示意图是这样的: 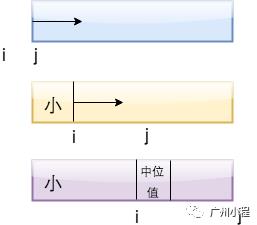
按这种设计,可以这样写代码:
#include <iostream>
using namespace std;
template< typename T >
void Exchange(
T & leftElement,
T & rightElement
)
{
T temp = leftElement;
leftElement = rightElement;
rightElement = temp;
}
template< typename T >
int Partition(
T List[],
int nStartPos,
int nStopPos
)
{
if ( nStartPos < 0 || nStopPos < 0 )
return -1;
int nLessEndPos = nStartPos - 1;
int nCurrentDealPos = nStartPos;
while ( nCurrentDealPos < nStopPos )
{
if ( List[nCurrentDealPos] <= List[nStopPos] )
{
nLessEndPos ++;
Exchange( List[nLessEndPos], List[nCurrentDealPos] );
}
nCurrentDealPos ++;
}
Exchange( List[nLessEndPos+1], List[nStopPos] );
return nLessEndPos + 1;
}
template< typename T >
void QuickSort(
T List[],
int nStartPos,
int nStopPos
)
{
if ( nStartPos < nStopPos )
{
int nMidPos = Partition<T>( List, nStartPos, nStopPos );
QuickSort( List, nStartPos, nMidPos - 1 );
QuickSort( List, nMidPos + 1, nStopPos );
}
}
int main(int argc, const char *argv[])
{
int arr[] = {4, 2, 5, 1, 6, 6, 8, 9, 8, 3};
int size=sizeof arr/sizeof *arr;
for (int i = 0; i < size; i ++) {
printf("%d, ", arr[i]);
}
QuickSort<int>(arr, 0, size-1);
printf("\nafter_sort:\n");
for (int i = 0; i < size; i ++) {
printf("%d, ", arr[i]);
}
printf("\n");
return 0;
}
读者不必在意代码实现的语言细节,事实上,代码实现并不是小程介绍的重点。
至此,如何“定中位”的关键设计就介绍完毕了,而快排的设计套路也介绍到这里。
总结一下,本文介绍了快速排序的重要套路,也就是重用跟分治的套路,特别是分治的设计,因为它是经过精心设计的套路,并非简单的一分为二。另外,本文也介绍了快排的设计关键,也就是如何“定中位”。最后,演示了如何用代码实现快速排序的算法设计。
以上是关于快速排序的套路的主要内容,如果未能解决你的问题,请参考以下文章