快速排序算法的优化--三数取中法

Posted 2021-05-02 码道小鑫

当前浏览器不支持播放音乐或语音，请在微信或其他浏览器中播放

最近在刷《剑指offer》时发现快速排序出现的频率还是挺高的，以前学习的quickSort算法只是很初级，能够解决一些常规的数据排序，但是也存在一些比较普遍的特殊情况，例如给我们的数组的第一个位置或者最好一个位置的元素值非常小或者非常大，那么如果我们一味的把枢纽值--key设置为第一个位置的元素或最后一个元素位置那么在遍历一遍数组元素后就会把key放在最后面或者最前面，那么根据快速排序的思想--要把比key小的元素放在key的左边，把比key大的元素放在key的右边，此时我们的数组遍历后交换元素后就会只存在比key小或者比key大的一边元素，为了避免这种情况，可以把枢纽值key设定为我们在数组中选的三个元素中按大小排序后中间那个元素，这就保证了key的不至于太大，也不至于太小。最后也对初始快排算法中的交换元素进行处理，大大的增加了快排的性能。

　在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。

1. 三数取中
   

三数取中就是取数组中最左、中间、最右边的三个数，把这三个数进行递增排序，取排序后的中间的那个数作为快速排序的 枢纽key。
    首先比较数组第一数和最后一个数（先比较两边的数），把小的数放在最左边，保证第一个数小于最后一个数，然后拿中间数先与最后一个数比较
    确保中间的数小于最后一个数，然后在吧中间的数与第一个数比较（此时最左边的数已经是最小的数），如果中间数大于最左边的数，则交换，此时
    就是标杆了，因为我们设定第一个数是key

2.快速排序图解

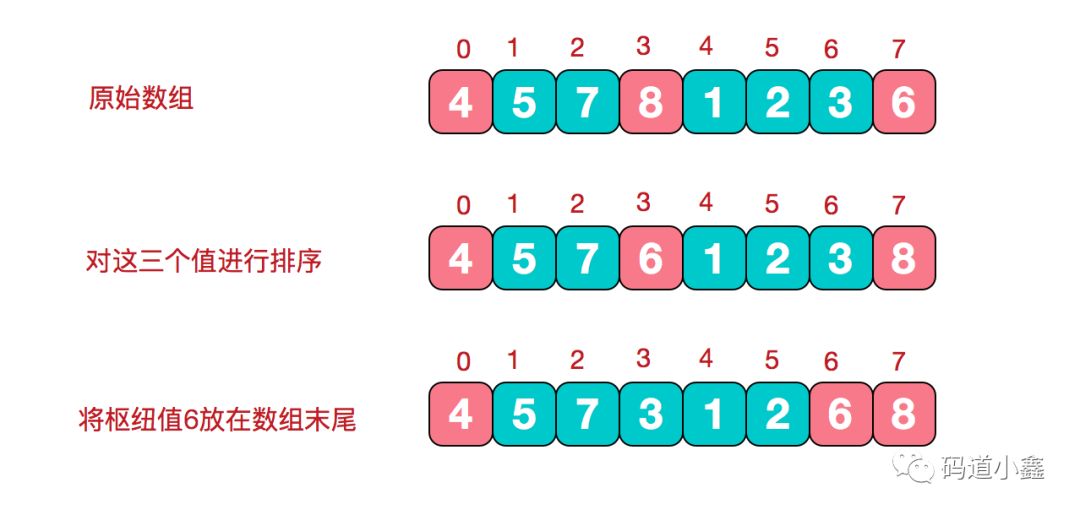
3.代码实现

package cn.dataStructures.Sort;

public class QuickSort1 {
    public static int quickSort(int[]arr,int low,int high){
        if(arr==null||arr.length<1)
            return 0;
        int start=low;
        int end=high;
        //去数组的中间值
        int mid=(high-low)/2;
        //确保三数中最左边的小于最右边
        if(arr[low]>arr[high])
            swap(arr,low,high);
        //确保三数中中间值小于最右边
        if(arr[mid]>arr[high])
            swap(arr,mid,high);
        //以上确定中间和最右边后，左边其实已经确定了为最小的元素，此时交换是因为我们取得枢纽值为数组的第一个元素
        if(arr[mid]>arr[low])
            swap(arr,low,mid);
        int key=arr[low];
        while(start<end){
            while(start<end&&arr[end]>=key)
                end--;
            arr[start]=arr[end];
            while(start<end&&arr[start]<=key)
                start++;
            arr[end]=arr[start];            
        }
        //把枢纽值赋值给此时的start位置--此时start与end都指向同一个元素
        arr[start]=key;
        if(low<start)
            quickSort(arr,low,start-1);
        if(end<high)
            quickSort(arr,end+1,high);
        //返回此时枢纽值再数组中对应的索引
        return start;    
    }
    //交换
    private static void swap(int []arr,int a,int b){
        int tem=arr[a];
        arr[a]=arr[b];
        arr[b]=tem;
        
    }
    //数组的打印方法
    public static void printSortArr(int []arr){
        StringBuilder res=new StringBuilder();
        res.append("[");
        for(int i=0;i<arr.length;i++){
            if(i==arr.length-1){
                res.append(arr[i]+"]");
            }
            else{
                res.append(arr[i]+",");
            }
        }
        System.out.println(res.toString());
    }
    public static void main(String[] args) {
        int []arr={2,11,3,11,44,22,5,2,55,24,19,200,100,33};
        System.out.println("排序前：");
        printSortArr(arr);
        System.out.println("排序后：");
        quickSort(arr,0,arr.length-1);
        printSortArr(arr);
    }
}

4.时间复杂度分析

快速排序的时间性能取决于快速排序的递归深度，对于一棵二叉树递归深度是log（n）+1（n为元素个数），对于数组元素个数为N，第一次需要遍历这个数组所有元素一遍，此时时间复杂度为O(n)那么进过深度为log（n）+1的递归后，总的时间复杂度为O(nlog(n)).

在最坏情况下--即数组是已经排好序了，正序或者逆序，如果换成树就是一棵斜树，左斜树和右斜树，此时需要n-1次递归调用，第i次划分需要第n-i次元素的比较，此时时间复杂度为O(n^2).

综合以上平均情况下应该是枢纽值取第K个元素时，复杂度为O(nlog(n))，具体分析参考《大话数据结构》第422页。

最后快速排序算法是一种不稳定的排序算法，因为每次数组元素进行交换和比较时都是跳跃性的。