快速排序的举一反三
Posted 计算机考研助手
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了快速排序的举一反三相关的知识,希望对你有一定的参考价值。
1. 快速排序
快速排序的基本思想
给定一个任意顺序的序列 S, 快速排序的目的就是首先找到一个基准数据(默认选第一个数据)pivot,通过一次 partition 程序之后,这个序列会以基准数据 pivot 为边界将数据分为 S_left 和 S_right 左右两个部分。S_left 子序列中所有数据都小于等于 pivot 基准数据, S_right 子序列中的数据都大于等于 pivot 基准数据。然后再递归地处理 S_left 和 S_right 子序列, 直到子序列中只有一个元素。
举个例子, 假如序列 S 的的元素如下:
S = [5, 6, 5, 1, 2, 9, 8, 10]我们以 起始位置的 5 作为基准数据 pivot, 那么经过一次 partition 处理之后 S 的元素如下:
S = [1, 2, 5, 5 , 10], 6, 9, 8, 10]在上面的例子中,我们可以看出在基准数据 5 左边的数据均小于等于 5,右边的数据均大于等于 5,经过这次 partition 操作之后,基准数据的位置就确定了。在这个交换过程中,两个 5 的相对顺序也发生了变化,这说明快速排序是一种不稳定的排序算法。然后,我们需要继续对两个子序列
S_left = [1, 2, 5]S_right = [6, 9, 8, 10]
分别进行 partition 操作。一直递归下去,直到为每个子序列的基准数据都找到了合适的位置。
partition的基本思想及其实现
从上文可知,快速排序的本质就是根据基准数据将序列分成两部分,左边的所有数据都小于等于基准数据,右边的所有数据都大于等于基准数据。因此,partition 的过程其实就是对基准左右两端的数据中不满足上述条件的数据进行交换的过程。为了达到这一目的,我们可以设置两个哨兵 left 和 right。 初始时,哨兵 left 位于序列的最左端,哨兵 right 位于序列的最右端。哨兵 right 负责从右往左查找小于基准的数据项,哨兵 left 负责从左往右查找大于基准的数据项,然后将这两个不符合条件的数据项进行交换。直到两个哨兵相遇, 相遇的位置即为基准数据最后应该在的位置。具体实现过程如下:
int partition(std::vector<int> &nums, int beg, int end){if(beg == end){return beg;}int left = beg, right = end;int pivot = nums[beg];while(left < right){// 从右往左查找小于基准的数据项while(nums[right] >= pivot && left < right){right--;}// 从左往右查找大于基准的数据项while(nums[left] <= pivot && left < right){left++;}std::swap(nums[left], nums[right]);}std::swap(nums[beg], nums[left]);return left; //left==right}
快速排序的实现
通过上述分析可知,一次 patition 的过程本质上就是将基准数据归位。 快速排序可以看作是一个递归调用的过程,具体实现可以分为两个部分,首先利用 partiion 程序将当前序列的的基准数据进行归位,然后再递归调用该程序,分别处理左右两端的子序列。直到所有数据都归位为止, 具体实现如下:
void Qsort(std::vector<int> &nums, int beg, int end){if(beg >= end) return;int pivot_index = partition(nums, beg, end);Qsort(nums, beg, pivot_index - 1);Qsort(nums, pivot_index + 1, end);}
快速排序的平均时间复杂度分析
假设序列长度为 n, 快排的平均时间复杂度为 T(n),T(1) = 1。在上一部分我们可以看出,快速排序的时间消耗在两个部分,第一部分是 partition 算法, 因为要遍历一遍序列的元素,其时间复杂度为 O(n); 第二部分是处理两个子序列的时间,每一个子序列的平均时间复杂度为 T(n/2). 因此,T(n) 的计算如下:
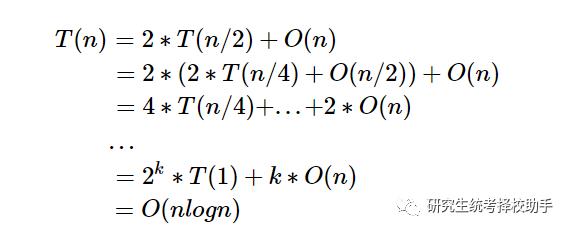
此处 2^k = n。
2. partition 的应用
从上文的分析我们可知,partion 的本质是通过基准数据对一个无序序列进行了分类, 其中的一类数据小于基准数据,另一类数据大于基准数据,而基准数据刚好位于这两类数据的中间,而这个中间位置刚好就是是所有数据都有序之后,基准数据的所在位置。从这个意义上来说,快速排序可以看作是对 partion 的一种应用。
在一个无序序列中查找某些符合条件的数据是一种常见的算法题型,比如查找第 k 大的数据,计算一个序列的中位数,找出最小的 k 个数等等。在一个有 n 个元素的序列中查找第 k(0 <= k < n) 大的元素,你可以首先对序列进行排序,然后再取出第 k 个元素,此时的时间复杂度取决于你选择的排序算法。 如果你采用快速排序则为O(nlogn)。下面我们看一下如何使用 partition 来完成这个任务。
一次 partition 之后我们可以确定基准数据的位置 pivot_index,如果 pivot_index 等于 k 刚好找到,如果 pivot_index 大于 k 则说明第 k个 的数据应该在基准的左边,否则在基准的右边。一个朴素的实现版本如下:
int find_kth_value(std::vector<int> &nums, int beg, int end, int k){int pivot_index = partition(nums, beg, end);if(pivot_index = k){return nums[k];}else if(pivot_index > k){//k_th value应该在基准的左边return find_kth_value(nums, beg, pivot_index - 1, k);}else{//k_th value应该在基准的左边return find_kth_value(nums, beg, pivot_index - 1, k);}}
而中位数的题则可以看成是第 k 大数据的一个特殊情况。下面我们来分析一下这个算法的平均时间复杂度情况:
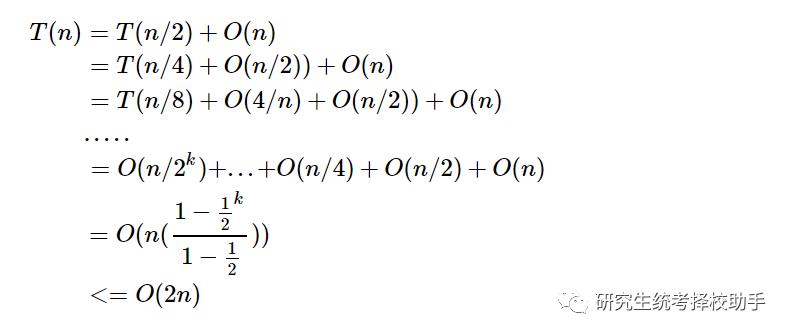 所以这是一个O(n)级别的算法,与直接用排序相比,基于 partition 的解法具有较低的时间复杂度。
所以这是一个O(n)级别的算法,与直接用排序相比,基于 partition 的解法具有较低的时间复杂度。
重要的事情重复三遍:
如果你想在一个无序的序列中查找某些目标数据,partition 算法可以帮你快速缩小目标范围,降低算法的平均时间复杂度!
如果你想在一个无序的序列中查找某些目标数据,partition 算法可以帮你快速缩小目标范围,降低算法的平均时间复杂度!
如果你想在一个无序的序列中查找某些目标数据,partition 算法可以帮你快速缩小目标范围,降低算法的平均时间复杂度!
至于如何在有序序列中缩小目标范围,请继续关注下期对二分查找的举一反三。
深圳大学 560801876
上海大学 772892871
浙江大学 716278248
杭州电子科技大学 580950115
电子科技大学 720797104
西安电子科技大学 157491662
北京邮电大学 739981211
南京大学 852875797
西安交通大学 305174352
吉林大学 731165424
合肥工业大学 581517900
郑州大学 695292662
中国科学技术大学 685573929
安徽大学 697570596
计算机考研报考院校分析系列文章如下:
持续更新…………
计算机考研交流群: 707803886
院校考研交流群:
以上是关于快速排序的举一反三的主要内容,如果未能解决你的问题,请参考以下文章